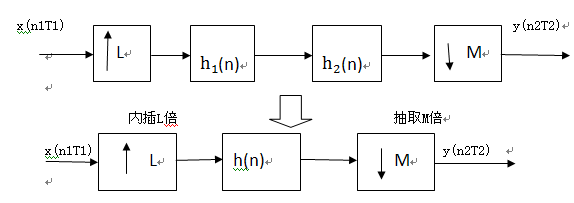
【转载】我见之采样率转换
在数字信号处理的许多实际应用中,我们面临着改变信号采样率的问题,或者增加一定的量或者减少一定的量。对模拟信号进行数字处理,提高处理速度是实现实时处理的首要目的。此外,减小存储容量,减少有限字长效应影响,实现不同系统互相兼容都是我们需要解决的问题。在数字电话系统中,传输的信号既有语音信号,又有传真信号,甚至有视频信号,这些信号的频率成分相差甚远。以上所有问题的解决都有必要使用多采样率理论来实现采样率的转换,从而使系统工作在多采样率状态
为了使采样率转换前后的信号及其频谱的性质清晰明了,特运用Matlab工具软件对多采样化进行了仿真。以下篇幅列举几种实现采样率转换的方法。
(1)Decimate
MATLAB7. 0信号处理工具箱提供了抽取函数decimate,用于信号整数倍抽取,其调用格式为:
y=decimate(x,M) ,
y=decimate(x,M,n),
y=decimate(x,M,’fir’),
y=decimate(x,L,n,’fir’) ,
其中y=decimate(x,M)将信号x的采样率降为原来的1/M。在抽取前缺省地采用了8阶ChebyshevⅠ型低通滤波器;
y = decimate (x,M,’fir’)采用指定的30点滤波器来压缩频带;
y = decimate (x,L,n,’fir’)指定所使用的Fir滤波器的点数。
若通过仿真结果可以清楚的看到抽取后的时域信号的数据量大大减少,而在抽样前后频谱的比较过程中可以进一步发现,抽取前后频谱只是发生了水平拉伸和幅度压缩。由此可见,给予一定的控制,抽取过程仅仅改变了要处理数据的大小,而并不丢失信号所携带的信息。
(2)Interp
整数倍内插是整数倍的抽取的逆过程,其实现原理与整数倍抽取类似,主要通过使用interp函数,使序列的采样率提高到原采样率的一定倍数,从而达到技术上要求。
Interp的调用格式为:
y=interp(x,L),
y=interp(x,L,n,alpha),
其中,y =interp(x,L)将信号的采样率提高到原来的L倍;
若采用仿真可以得出如下结论: a与b相比较,采样率提高了一倍,再将图c与d相比较会发现,内插前后信号不会发生丢失或增加,只是频谱在一定程度上压缩了。
(3)Intfilt函数
该函数用于设计线性相位Fir滤波器,并对理想带限信号插值后平滑,调用格式为:
y=intfilt(r,n,‘Laguage’),
y=intfilt(r,l,alpha)。
引用格式y=intfilt(r,l,alpha)内插是在相邻的两点之间插入r-1个零值点,然后用2*r-1、归一化截止频率为alpha的Fir滤波器进行滤波。而调用格式y=intfilt(r,n,‘Laguage’)则是设计n阶Fir滤波器,当n为偶数时,y的长度为(n+1)*r,当n为奇数时,y的长为:(n+1)*r-1,函数生成的都是低通Fir滤波器,专门用于内插。
利用intfilt函数内插滤波后的波形仿真。此过程使用带限方法,设计插值滤波器,使采样率变为原来的4倍。
(4)Firdn函数
y=upfirdn(x,h),
y=upfirdn(x,h,p),
y=upfirdn(x,h,p,q) 。
该函数执行时有以下三个步骤:
a、对x向量进行上采样,使采样率变为原来的p倍;
b、对内插后的数据进行滤波,滤波器的冲激响应向量为h;
c、对滤波器结果进行下采样抽取,使频率降低q倍。
(5)Mfilt函数
函数调用格式为y=mfilt(structure(input1,input2,···) )
该函数执行时有以下3个步骤:
a、对x向量进行上采样内插,采样率变为原来的p倍;
b、对内插后的数据进行滤波,滤波器的冲激响应向量为h;
c、对滤波器结果进行下采样抽取,使频率降低q倍。
经过仿真,多采样率转换得以很好的实现,并且体现了其方便性,可选择性、为多采样率理论的广泛应用作好了铺垫。
(6)Resample函数
函数调用格式为:
y=resample(x,L,M)
y=resample(x,L,M,n)
y=resample(x,L,M,n,beta)
y=resample(x,L,M,b)
[y,b]=resample(x,L,M)
其中,y=resample(x,L,M)将信号x的采样率转换为原来的L/M倍,所用的低通滤波器为kaiser窗的滤波器;
y=resample(x,L,M,n)指定用左右两边各n个数据作为冲采样的领域;
y=resample(x,L,M,n,beta)指定kaiser窗FIR滤波器的设计参数,缺省值为5;
y=resample(x,L,M,b)指定用于重采样的滤波器系数向量;
[y,b]=resample(x,L,M)除得到重采样信号y外,还返回所使用的滤波器系数向量b;