POJ 3204 Road Reconstruction-网络流-最小割边集

题意

一个由n个点，m条边构 成的有向图，每条边都有一定的流量。现在求存在多少条边，在增加这些边的流量后从1点到n的总流量会增加。

分析

先求最大流。在得到最大流f后的残量网络G_f中，从s开始DFS，所有能遍历到的点构成点集S。没有搜索到的构成点集T，两集合间的边构成最小割边集。
注意：虽然 最小割[S,T]的边都是满流边，但是满流边不一定是最小割边集。如下面的二分图的例子

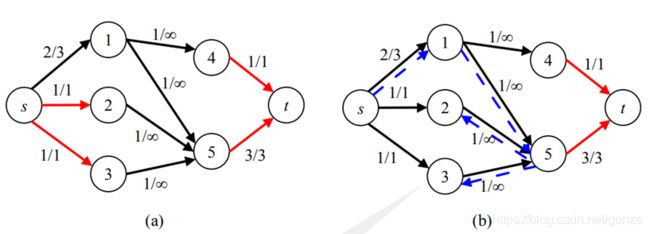
图(a)给出了一个基于二分图构造的流网络。由于从X部到Y部都是容量均为正无限的边，都不可能是最小割中的边，有人便会错误地认为与源或汇关联的满流边便组成了最小割（图(a)的红色边）。然而实际上，在该网络的残留网络中，结点2与3应该与源s是连通的（图(b)的蓝色路径），所以最小割应该是图(b)中的红色边。

【本题做法】
做一次最大流
S出发dfs正向边，标记搜索到的点集S’
T出发dfs反向边，标记搜索到的点集T’
枚举所有的边，如果一条边的端点属于不同的点集，且该边为满流，则是割边

参考代码

#include
#include
#include
#include
#include
using namespace std;
#define ll long long
#define in rad()
inline int rad(){
	int x=0,f=1;char c=getchar();while(c>'9'||c<'0')c=getchar();
	if(c=='-')f=-1,c=getchar();while(c>='0'&&c<='9')x=x*10+c-48,c=getchar();
	return x*f;
}
const int maxn=1e5+10;
const int maxm=4e6+100;
const int inf=1e9;
struct Edge {
	int u,v,w,nxt;
} e[maxm];
int first[maxn]= {},cnt=1,S,T;
inline void add(int u,int v,int w) {
	e[++cnt].v=v;e[cnt].u=u;e[cnt].w=w;e[cnt].nxt=first[u];first[u]=cnt;
}
inline void ins(int u,int v,int w){
	add(u,v,w);add(v,u,0);
}
int n,m;
namespace D{
	int dis[maxn],cur[maxn];
	int bfs(int s,int t){
		memset(dis,-1,sizeof(dis));
		queue<int>q;
		dis[s]=0;q.push(s);
		while(!q.empty()){
			int u=q.front();q.pop();
			for(int i=first[u];i;i=e[i].nxt){
				int v=e[i].v;
				if(dis[v]!=-1||e[i].w==0)continue;
				dis[v]=dis[u]+1;
				q.push(v);
				if(v==t)return 1;
			}
		}
		return 0;
	} 
	int dfs(int u,int t,int f){
		if(!f||u==t)return f;
		int w,used=0;
		for(int &i=cur[u];i;i=e[i].nxt){
			int v=e[i].v;
			if(dis[v]!=dis[u]+1||e[i].w==0)continue;
			w=dfs(v,t,min(f,e[i].w));
			used+=w;f-=w;
			e[i].w-=w;e[i^1].w+=w;
			if(f==0)break;
		}
		return used;
	}
	int dinic(int s,int t){
		int ret=0;
		while(bfs(s,t)){
			memcpy(cur,first,sizeof(first));
			ret+=dfs(s,t,inf);
		}
		return ret;
	}
}
int f1[maxn],f2[maxn],vis[maxn];
void dfs(int u,int f[],int d){
	f[u]=1	;
	for(int i=first[u];i;i=e[i].nxt){
		int v=e[i].v;
		if(e[i^d].w&&!f[v])dfs(v,f,d);
	}
}
 
int main(){
	n=in;m=in;
	for(int i=1;i<=m;i++){
		int u=in,v=in,w=in;
		ins(u,v,w);
	}
	D::dinic(0,n-1);
	dfs(0,f1,0);
	memset(vis,0,sizeof(vis));
	dfs(n-1,f2,1);
	int ans=0;
	for(int i=2;i<=cnt;i+=2)
		if(f1[e[i].u]&&f2[e[i].v] && e[i].w==0)ans++;
	cout<<ans;
	return 0;
}