bzoj1095 线段树括号序列

题目分析

首先%%% 岛姐的讲解
然后%%% hzwer的代码
最后%%% 树王的帮助
好吧，写写我的感悟。

括号序列与距离

首先我们对于一棵美丽的树，可以生成一个先序遍历的括号序列，左括号表示到达该店，右括号表示离开该点。例如下图这棵美丽的树，可以生成一个这样的序列：（1（2（3）（5））（4）（6（7）））

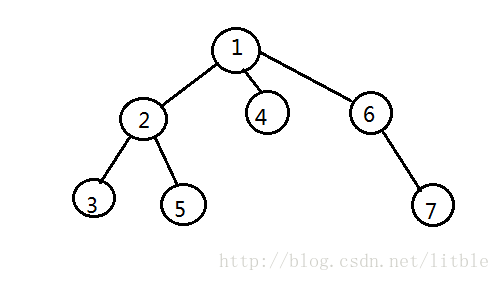
这个序列有什么用呢？两个点之间的距离，就是它们之间括号序列去掉可以匹配的括号后的括号数。这是为什么呢？是因为两个点之间的路径相当于遇到左括号向下走，遇到右括号向下走，匹配的括号即走了来回没有必要。
例如上图3和4节点，之间的括号为）（））（，去掉匹配的得到））（，即他们之间的距离为3.

括号序列与线段树

好了，那么我们要求的是最远的两个黑点之间的距离dis（左区间dis，右区间dis，横跨左右区间的dis）。
先不考虑黑点。
既然这样，那么我们当然要用线段树维护某两个点之间的“去掉匹配的括号后的括号数”，设括号序列里的某一段S有c1个右括号，c2个左括号。在线段树里S被拆成左边是S1右边是S2，a1=S1.c，b1=S1.c2，a2=S2.c1，b2=S2.c2，a=S.c1，b=S.c2。合并S1与S2的时候因为要去掉匹配的括号，所以：
当b1>a2时，a=a1,b=b1+b2-a2;
否则，a=a1+a2-b1,b=b2;
这样就可以用线段树维护c1和c2了，鼓掌！！！！撒花！！！！

黑白点信息的维护

%了hzwer代码后，我发现可以额外开一个数组来表示每一个点是黑是白，更改方式可以看代码啦，我就不讲了，还是不难的。
所以我们主要就是讲updata函数。
首先，根据上面的式子可以发现，a+b=a1+b2+|b1-a2|=max((a1-b1)+(a2+b2),(a1+b1)+(b2-a2));这么一来，我们就知道我们要维护的东西了（因为维护dis的方法）：
l1:是该区间一段前缀，在这个前缀后面就是一个黑点，a+b。
l2:是该区间一段前缀，在这个前缀后面就是一个黑点，b-a。
r1:是该区间一段后缀，在这个后缀前面就是一个黑点，a+b。
r2:是该区间一段后缀，在这个后缀前面就是一个黑点，a-b。
那么：S.dis=max(S1.dis,S2.dis,S1.r1+S2.l2,S1.r2+S2.l1);
好的，那么我们怎么维护l1,l2,r1,r2呢？
由于a+b=max((a1-b1)+(a2+b2),(a1+b1)+(b2-a2)),所以：
S.l1=max(S1.l1，S2.l1+a1-b1，S2.l2+a1+b1); （左区间，横跨左右区间）
S.r1=max(S2.r1，S1.r2+a2+b2，S1.r1+b2-a1);
然后很容易得到：
S.l2=max(S2.r2，S1.r2+a2-b2);
S.r2=max(S1.l1，S2.l2+b1-a1);
因为写的比较快，如有误请指出并看代码。
好了，这个问题解决了。

代码

有一些内容是抄的hzwer的…

#include
#include
#include
#include
#include
using namespace std;
#define LL long long
const int N=100005;
int n,tot,now,black,m,inf=1000000000;
int c[N],h[N],ne[N<<1],to[N<<1],v[N*3],pos[N];
struct node{int c1,c2,l1,l2,r1,r2,dis;}tr[N*12];
//c1:右括号，c2：左括号
void add(int x,int y){to[++tot]=y,ne[tot]=h[x],h[x]=tot;}
void dfs(int x,int las){
    v[++now]=-1,v[++now]=x,pos[x]=now;
    for(int i=h[x];i;i=ne[i])
        if(to[i]!=las)dfs(to[i],x);
    v[++now]=-2;
}
void getdata(int x,int i){
    tr[i].dis=-inf,tr[i].c1=tr[i].c2=0;
    if(v[x]==-1)tr[i].c2=1;
    if(v[x]==-2)tr[i].c1=1;
    if(v[x]>0&&c[v[x]])tr[i].l1=tr[i].l2=tr[i].r1=tr[i].r2=0;
    else tr[i].l1=tr[i].l2=tr[i].r1=tr[i].r2=-inf;
}
void up(int i){
    int l=(i<<1),r=(i<<1)|1;
    int a1=tr[l].c1,b1=tr[l].c2,a2=tr[r].c1,b2=tr[r].c2;
    tr[i].dis=max(tr[l].r1+tr[r].l2,tr[l].r2+tr[r].l1);
    tr[i].dis=max(tr[l].dis,max(tr[i].dis,tr[r].dis));
    if(b1>a2)tr[i].c1=a1,tr[i].c2=b2+b1-a2;
    else tr[i].c1=a1+a2-b1,tr[i].c2=b2;
    tr[i].r1=max(tr[r].r1,max(tr[l].r2+a2+b2,tr[l].r1+b2-a2));
    tr[i].r2=max(tr[r].r2,tr[l].r2+a2-b2);
    tr[i].l1=max(tr[l].l1,max(tr[r].l1+a1-b1,tr[r].l2+a1+b1));
    tr[i].l2=max(tr[l].l2,tr[r].l2+b1-a1);
}
void build(int s,int t,int i){
    if(s==t){getdata(s,i);return;}
    int mid=(s+t)>>1;
    build(s,mid,i<<1),build(mid+1,t,(i<<1)|1);
    up(i);
}
void chan(int x,int s,int t,int i){
    if(s==t){getdata(s,i);return;}
    int mid=(s+t)>>1;
    if(x<=mid)chan(x,s,mid,i<<1);
    else chan(x,mid+1,t,(i<<1)|1);
    up(i);
}
int main(){
    int i,x,y;char ch[10];
    scanf("%d",&n),black=n;
    for(i=1;i<=n;++i)c[i]=1;
    for(i=1;iscanf("%d%d",&x,&y),add(x,y),add(y,x);
    dfs(1,-1),build(1,now,1);
    scanf("%d",&m);
    for(i=1;i<=m;++i){
        scanf("%s",ch);
        if(ch[0]=='C'){
            scanf("%d",&x);
            if(c[x])--black;
            else ++black;
            c[x]^=1;
            chan(pos[x],1,now,1);//注意这里是pos[x]！！！
        }
        else {
            if(!black)printf("-1\n");
            else if(black==1)printf("0\n");
            else printf("%d\n",tr[1].dis);
        }
    }
    return 0;
}