算法基础:BFS和DFS的直观解释
一、前言
我们首次接触 BFS 和 DFS 时,应该是在数据结构课上讲的 “图的遍历”。还有就是刷题的时候,遍历二叉树我们会经常用到BFS和DFS。它们的实现都很简单,这里我就不哆嗦去贴代码了。
BFS和DFS是图的两种遍历方式,是最简单的图搜索算法。
BFS和DFS有几种实现方式,比如:
1、使用队列Queue实现图的BFS遍历
2、递归实现图的DFS遍历
3、使用栈Stack迭代实现图的DFS遍历
本篇文章就单纯来讲讲它们的区别和各自的应用,不会涉及任何代码。我们以“图的遍历”为例,进行说明。
二、区别
广度优先搜索算法(Breadth-First-Search,缩写为 BFS),是一种利用队列实现的搜索算法。简单来说,其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。
深度优先搜索算法(Depth-First-Search,缩写为 DFS),是一种利用递归实现的搜索算法。简单来说,其搜索过程和 “不撞南墙不回头” 类似。
BFS 的重点在于队列,而 DFS 的重点在于递归。这是它们的本质区别。
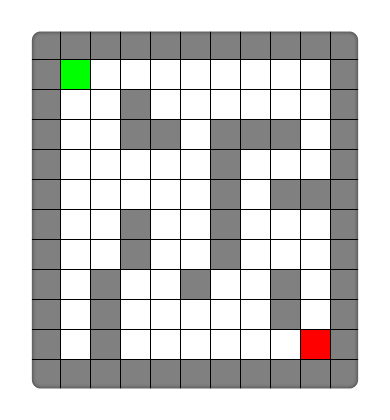
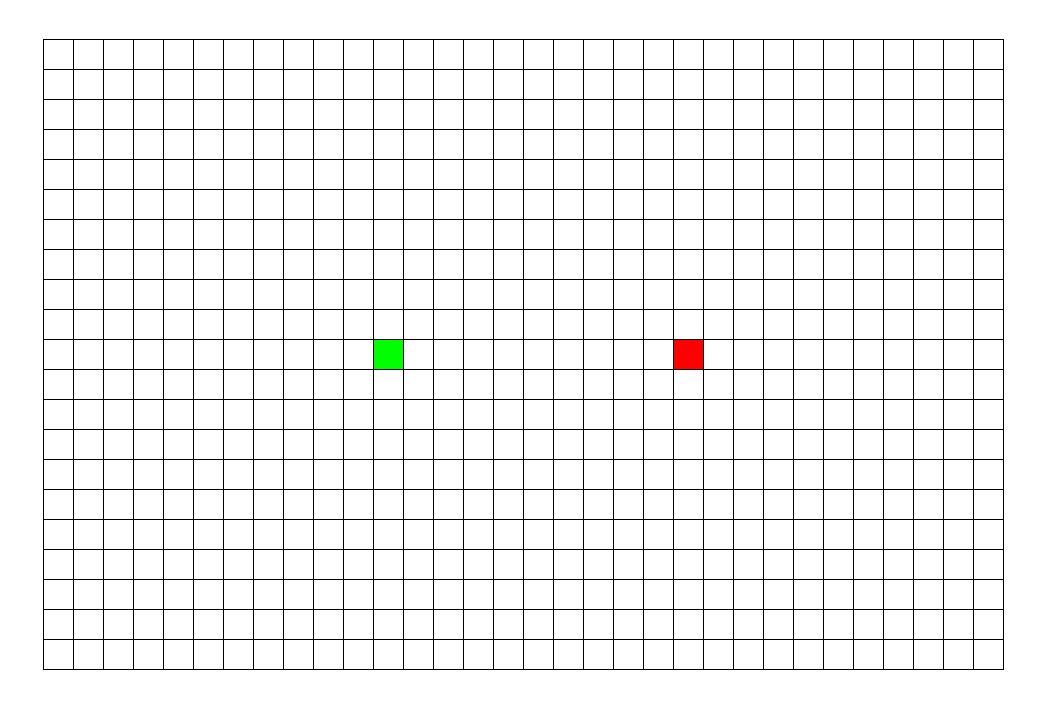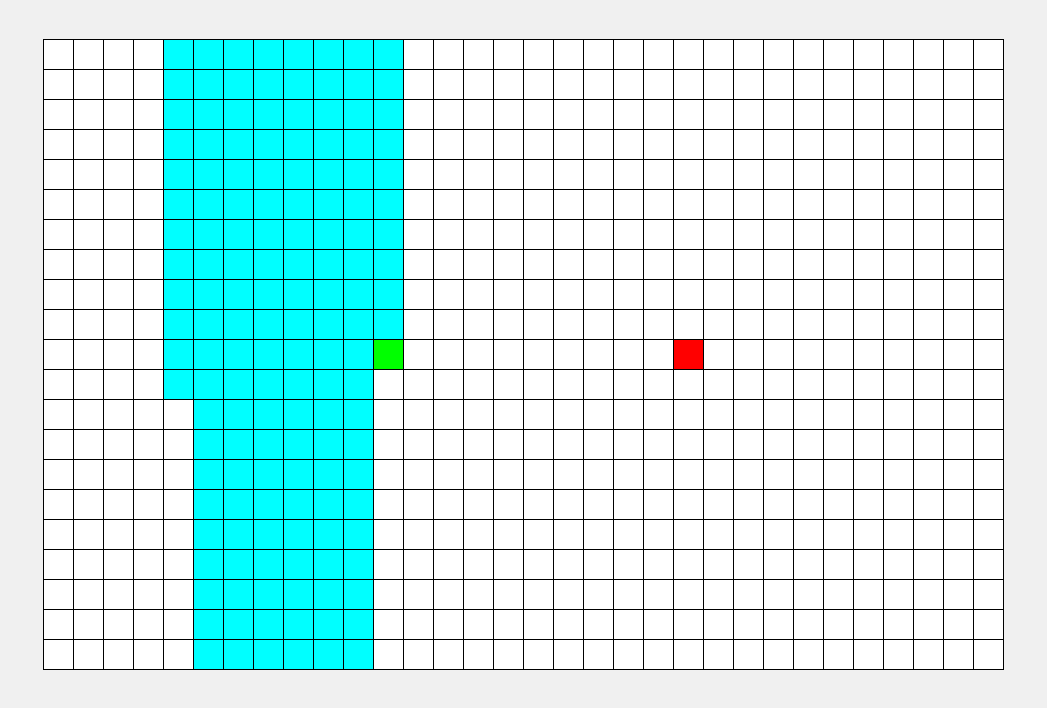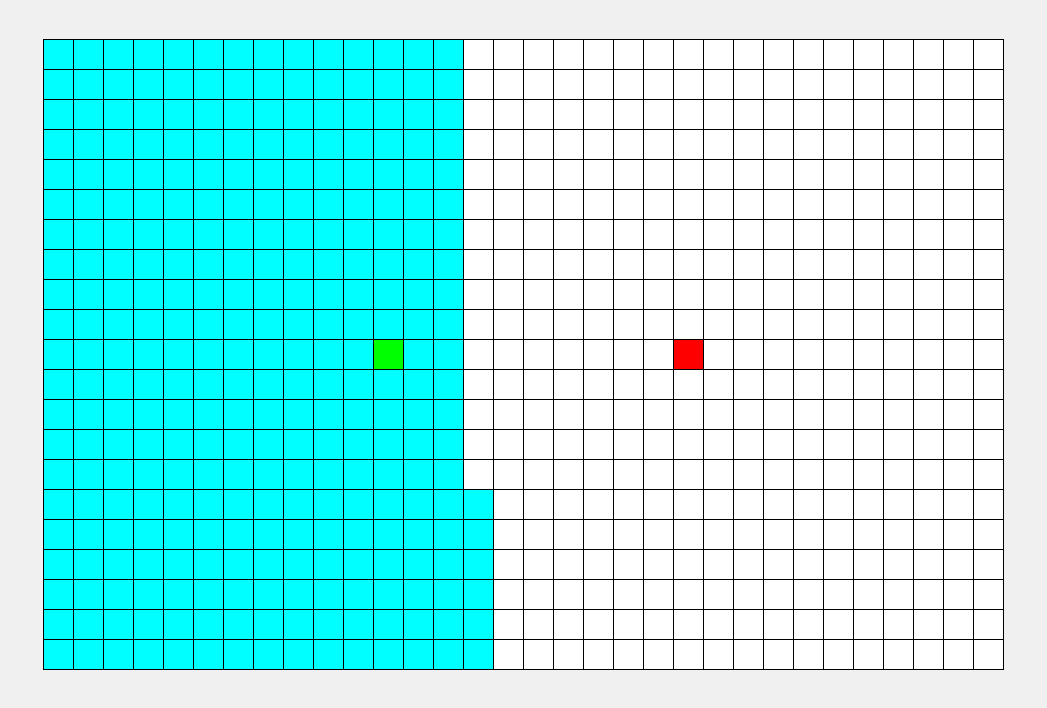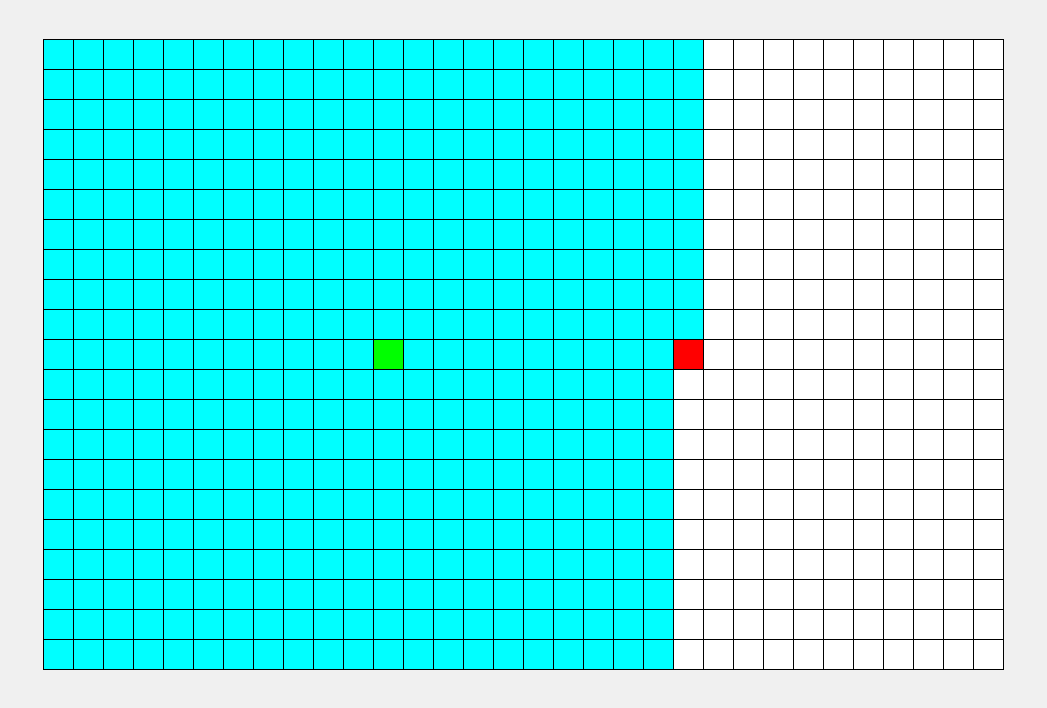
举个典型例子,如下图,灰色代表墙壁,绿色代表起点,红色代表终点,规定每次只能走一步,且只能往下或右走。求一条绿色到红色的最短路径。
对于上面的问题,BFS 和 DFS 都可以求出结果,它们的区别就是在复杂度上存在差异。我可以先告诉你,该题 BFS 是较佳算法。
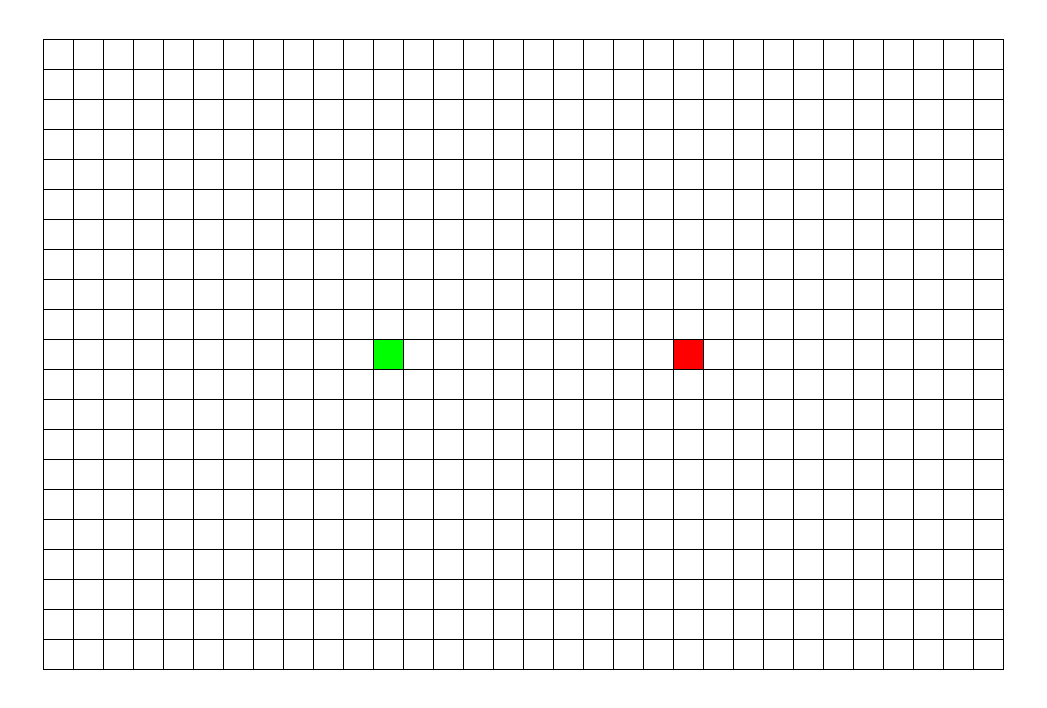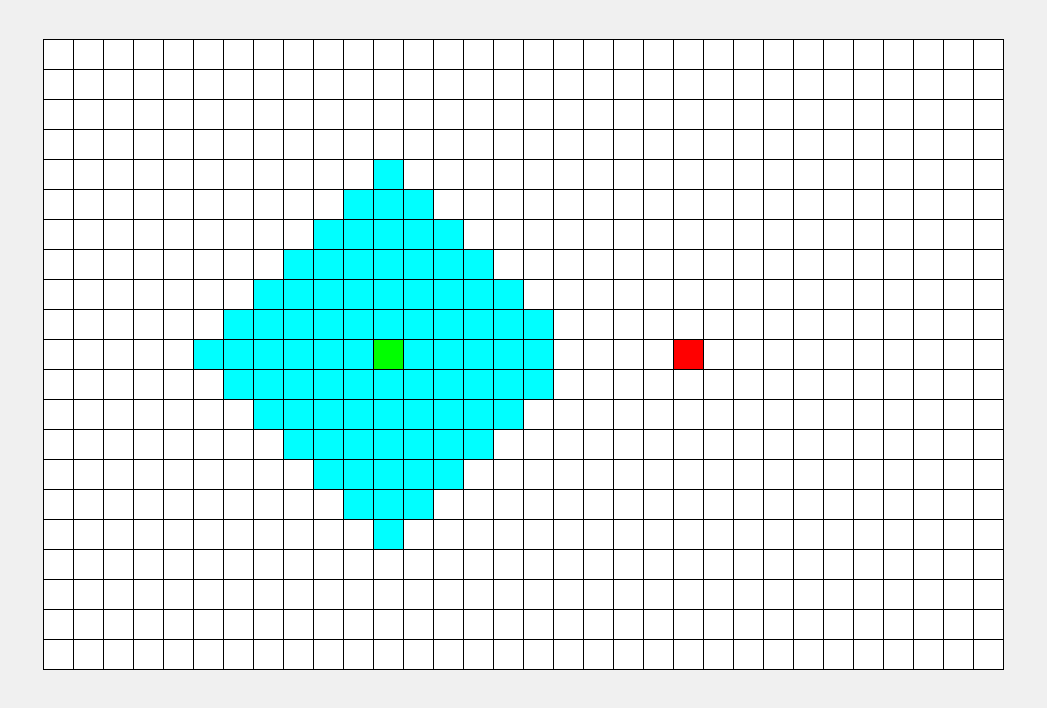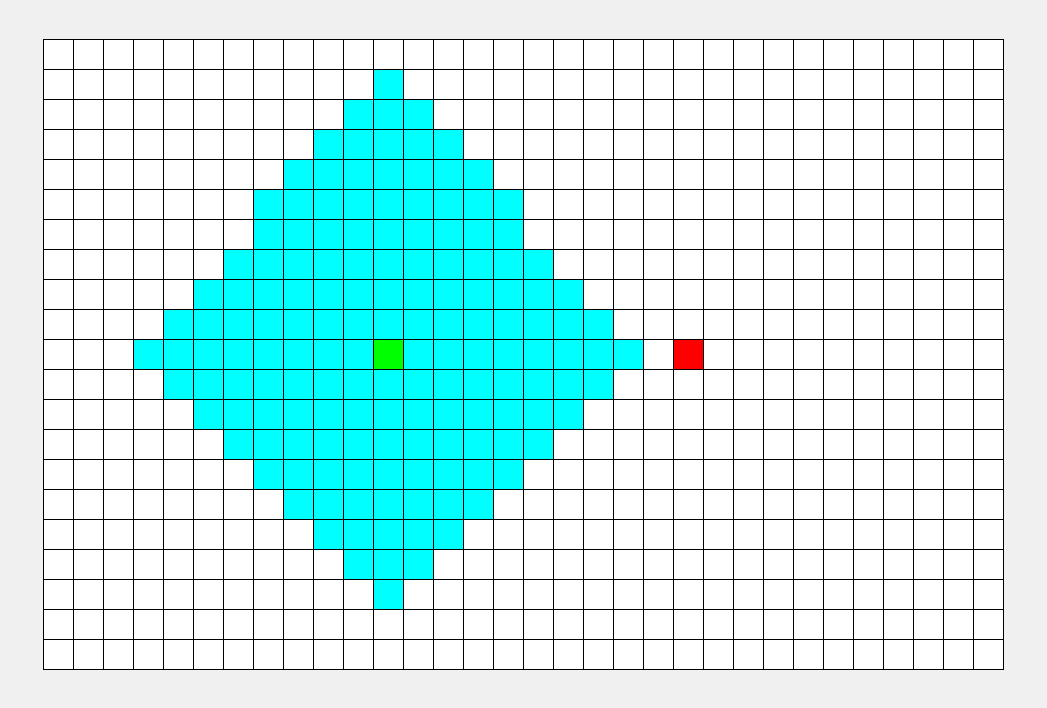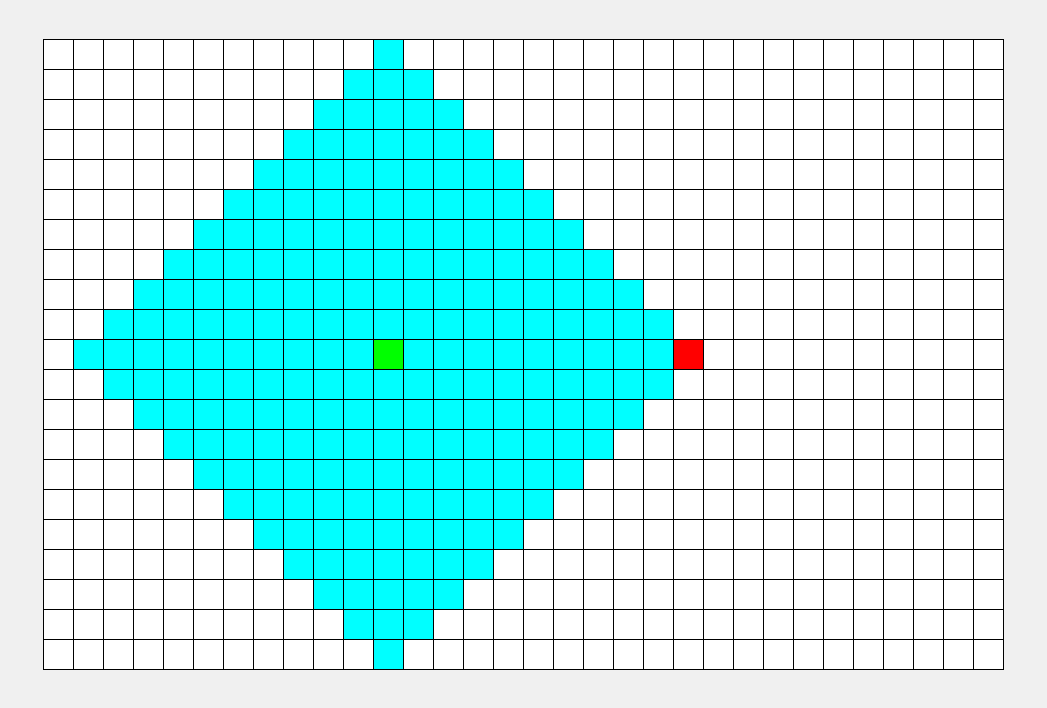
BFS示意图:
如上图所示,从起点出发,对于每次出队列的点,都要遍历其四周的点。所以说 BFS 的搜索过程和 “湖面丢进一块石头激起层层涟漪” 很相似,此即 “广度优先搜索算法” 中“广度”的由来。
DFS示意图:
如上图所示,从起点出发,先把一个方向的点都遍历完才会改变方向...... 所以说,DFS 的搜索过程和 “不撞南墙不回头” 很相似,此即 “深度优先搜索算法” 中“深度”的由来。
三、总结
现在,你不妨对照着图,再去看看你打印出的遍历序列,是不是一目了然呢?
最后再说下它们的应用方向。
BFS 常用于找单一的最短路线,它的特点是 "搜到就是最优解",而 DFS 用于找所有解的问题,它的空间效率高,而且找到的不一定是最优解,必须记录并完成整个搜索,故一般情况下,深搜需要非常高效的剪枝(剪枝的概念请百度)。
总的来说,BFS多用于寻找最短路径的问题,DFS多用于快速发现底部节点。
bfs是用来搜索最短径路的解是比较合适的,比如求最少步数的解,最少交换次数的解,因为bfs搜索过程中遇到的解一定是离最初位置最近的,所以遇到一个解,一定就是最优解,此时搜索算法可以终止,而如果用dfs,会搜一些其他的位置,需要搜很多次,然后还要一个东西来记录这次找的位置,之后找到的还要和这次找到的进行比较,这样就比较麻烦
dfs合搜索全部的解,因为要搜索全部的解,在记录路径的时候也会简单一点,而bfs搜索过程中,遇到离根最近的解,并没有什么用,也必须遍历完整棵搜索树。
bfs是舍弃时间换取空间,bfs是舍去空间换取时间。因为dfs要走很多的路径,可能都是没用的,(做有些题目的时候要进行剪枝,就是确定不符合条件的就可以推出,以免浪费时间,否则有些题目会TLE);而bfs可以走的点要存起来,需要队列,因此需要空间来储存,但是快一点。
稍微理解之后就可以了,不一定要纠结怎么用,先去做题目,很多都是做着就突然明白怎么用了。
PS:BFS 和 DFS 是很重要的算法,读者如果想要更深入地了解它们,建议去 OJ 或 Leetcode 上找一些相关赛题训练下,一定会给你一个别样的天地。
深度优先搜索
深度优先搜索算法(Depth First Search),是图论中的经典算法。
深度优先搜索算法是沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当结点所有子结点那一层都被搜索过,再回溯返回到当前结点的邻结点,继续搜索,直到遍历完整棵树。一般采用的是前序遍历,先根然后再左右结点的方式进行。
一些经典的问题,比如八皇后、马走日、迷宫等,都可以通过深度优先搜索算法来解决。
为了方便描述,下文用DFS来做为深度优先搜索算法的简称。
我对DFS的认识
对于DFS,我相信很多人第一次接触很难设计出相应的算法,即便是有不错的编程经验。我第一次几乎没办法设计出解决八皇后的算法,即便是想了很久。最后没办法只好参照别人写的递归式的DFS。之后,虽然对这个算法有一点了解,但由于了解不够深度,过了几天就记不得了,下次又完全不知道怎么入手。然后需要再到网上搜下代码,看一遍后大概才双知道。而且发现每次写代码的时候心里总觉得不踏实,一开始总有错误的地方,并且每次写的代码都有些不同。总之,写过很多次后,依然是停留到了解的阶段,没办法进一步提升,特别是非递归式的DFS一直都停留到靠脑力记忆而不是理解的阶段。
今天周末有点时间,觉得有必要解决这些问题,试着花时间去归纳总结DFS的本质,看能否做到一劳永逸。
我设定的目标是:
- 不仅停留到理解阶段,而是要知道这个算法每一步的实现
- 捉住其中的本质,给出这个算法的设计框架。
- 在1与2的基础中,可以熟练写出递归与非递归两种实现方式 。
经过一个下午的研究,我发现任何DFS只需要通过下面几步就可以实现,无论是递归还是非递归方式。我给这几步分别做了一个命名,分别是find、forward、done、back。
如下:
- find(right): 在树的当前层,横向遍历,尝试找到ok的节点。(这一步通常被叫做剪枝,只留下ok的。)
- forward(down): 若在当前层找到ok的结点且当前层不是最后一层,则把ok的节点放到当前层;进入下一层第一个结点,跳到find
- done(right): 若在当前层找到ok的结点,并且当前层是最后一层:打印出结果;进入当前层的下一个结点。跳到find
- back(up):在当前层没有找到ok的节点:返回上一层当前结点的下一个兄弟节点。跳到find。
其实最重要的是find。然后后面的forward、done、back只是用来控制搜索走向。这四步可以进一步总结成两步。
为了了解算法,我想最好的切入方式是从一些实例开始。下面分别从八皇后以及马走日等问题做为切入点来分析DFS
问题举例
用DFS解八皇后
1、问题描述
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?
也就是说,使得棋盘中每个横向、纵向、左上至右下斜向、右上至左下斜向均只有一枚皇后。
八皇后有92组解,下面给出其中一种解的图例:
作者:白马游侠
链接:https://www.jianshu.com/p/23394b9e233a
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。