超详细Tarjan算法总结，求强连通分量，割点，割边，有重边的割边

Tarjan是一个人，他一身中发明了很多算法，就这几个算法最为出名。

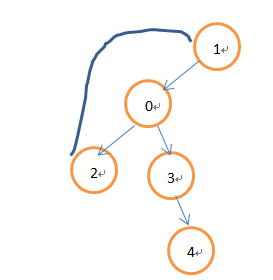
1、求有向图的强连通分量，那么什么是强连通分量呢，就是一个顶点集合，任意两个顶点间都可以互相到达。一个顶点也是强联通分量如果图中任意两点可以互相到达，则此图强连通。下图中顶点{1,0,2}属于一个强联通分量，{3}，{4}也属于；

TARJAN是基于dfs算法的基础上，所以也会得到一颗搜索树。如右边图

那么他是怎么运行的呢，首先大家看着两个数组 

dfn[i],和low[i]；一开始dfn【i】=low【i】=cnt++；

dfn[i]表示第i个节点深搜的顺序。例如根据右图深搜的顺序可以得到dfn【1】=1；dfn【0】=2；dfn【2】=3；依次类推下去；

low【i】表示i节点能够追溯到那个强联通分量最先访问的那个点的dfn值；因为他们是强联通分量所以他们一定会有环。既low【2】=dfn【1】=1；low【0】=low【2】=dfn【1】=1；  low【3】=dfn【3】=4；的值就不会改变因为她下面的点没有边能够连接到他的祖先上去，也是因为没有环。low【4】得值也不会改变；

大家此时有没有发现一个规律 既 每个强联通分量的第一个访问的那个次序low【i】都会等于dfn【i】；这里有三个想等所以他们有三个强联通分量。

具体操作大家看下面配合代码的具体演示吧；

代码:

void Tarjan(int u)//此代码仅供参考
{
    vis[u]=1;
    low[u]=dfn[u]=cnt++;
    for(int i=0;iif(vis[v]==1)  low【u】=min（low【u】，dfn【v】）；
   }
    if(dfn[u]==low[u])
    {
        sig++;
    }
}

代码模拟一遍哈！！！ 请大家认真仔细的用笔写，看哈；首先执行tarjan（u）;此时u等于1；执行low【1】=dfn【1】=1；将这个顶点标记为已经访问过

vis【1】=1；

节点0有没有被访问过，节点0没有被访问过往下面深搜此时搜到0，执行tarjan(0)；执行low【0】=dfn【0】=2；继续判断

继续深搜执行low【2】=dfn【2】=3；关键的来了哈，此时节点2继续往下面深搜 搜到了节点1；但是1已经被访问过了，就不继续深搜了。执行low【2】=min（low【2】，dfn【1】）；所以low【3】此时被赋值为1；然后第三层tarjan的循环语句结束了。执行判断dfn【3】是不是等于low【3】；这里是不等于所以计数器不增加；现在返回到第二层tarjan此时刚执行完tarjan【2】；接着更新low【0】则执行low【0】=min（low【0】，low【2】）；现在继续循环v=3；判断v有没有被访问过这里是没有被访问过执行tarjan（3）；接着low【3】=dfn【3】=4；然后进入循环体 v=4；然后节点4没有被访问过执行tarjan（4）；low【4】=dfn【4】=5；接着进入循环体，因为下面没有节点与4相连则退出循环体；则执行判断low【4】==dfn【4】此时他们想等计数器加1；接着返回到tarja（3）；执行low【3】=min（low【3】，low【4】）因为节点4没有往上面去的边，所以low【4】还是等于4并且大于low【3】；此时的low【3】也是同理不变；此时这个循环体也执行完了此时判断low【3】==dfn【3】这里是想等的所以计数器增加1；

此时函数返回到tarjan（0）；在执行low【0】=min（low【3】）；此时low【0】=1小于low【3】；则不更新low【0】；现在循环体也执行完了判断low【0】==dfn【0】；这里是不相等的；计数器不加；返回到tarjan（1）；此时他的循环体执行完了判断low【1】==dfn【1】；这里是想等计数器加1；最后求得强联通分量的个数为3；然后返回到主函数；以上就是tarjan算法的执行过程；

那么大家有没有想过万一图不连通呢；

所以我们在外面的这样处理  在外面加入一个循环；

代码；

#include//此代码仅供参考，用于求一个图存在多少个强连通分量
#include
#include
#include
using namespace std;
#define maxn 1000000
vectormp[maxn];
int ans[maxn];
int vis[maxn];
int dfn[maxn];
int low[maxn];
int n,m,tt,cnt,sig;
void init()
{
    memset(low,0,sizeof(low));
    memset(dfn,0,sizeof(dfn));
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)mp[i].clear();
}
void Tarjan(int u)
{
    vis[u]=1;
    low[u]=dfn[u]=cnt++;
    for(int i=0;i

这里求强联通分量就将讲到这里了；

推荐大家入门题目；hdu迷宫城堡；传送门http://blog.csdn.net/lw277232240/article/details/72123936

下面我们求割点；

割点什么是割点呢；就是在一个连通图中删除一个点就导致真个图不连通了，那么这个点就叫做割点；下图实边为dfs搜索的边，虚线边为回边，既可以访问父亲的祖先的边；

例如下图的A就是一个割点；

该算法是R.Tarjan发明的。观察DFS搜索树，我们可以发现有两类节点可以成为割点：

1. 对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；
2. 对非叶子节点u（非根节点），若其子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与u的子树的节点不再连通；则节点u为割点。

对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。

我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点（即DFS次序号最小），这里的dfn  low 跟上面的功能是一样的。，那么low[u]的计算过程如下：

low[u]={min{low[u], low[v]}min{low[u], dfn[v]}(u,v)为树边(u,v)为回边且v不为u的父亲节点low[u]={min{low[u], low[v]}(u,v)为树边min{low[u], dfn[v]}(u,v)为回边且v不为u的父亲节点

下表给出图(a)对应的dfn与low数组值。

i	0	1	2	3	4	5	6	7	8	9	10	11	12
vertex	A	B	C	D	E	F	G	H	I	J	K	L	M
dfn[i]	1	5	12	10	11	13	8	6	9	4	7	2	3
low[i]	1	1	1	5	5	1	5	5	8	2	5	1	1

对于情况2，当(u,v)为树边且low[v] >= dfn[u]时，节点u才为割点。该式子的含义：以节点v为根的子树所能追溯到最早的祖先节点要么为v要么为u。

代码：

void tarjan(int u,int pre)
{
    dfn[u]=low[u]=cnt++;
    vis[u]=1;
    for(int i=0;i=dfn[u]) cut[u]++;//这里是不是跟 切low[a]>=dfn[u],那么这个点u就是割点，这里是统计割点的个数就执行cut【u】++
        }
        else {
               low[u]=min(low[u],dfn[a]);
             }
    }
   if(pre==u) cut[pre]=gen-1;

}