软件测试基础知识——黑盒测试

黑盒测试定义
黑盒测试也称功能测试，它是通过测试来检测每个功能是否都能正常使用。
在测试中，把程序看作一个不能打开的黑盒子，在完全不考虑程序内部结构和内部特性的情况下，在程序接口进行测试，它只检查程序功能是否按照需求规格说明书的规定正常使用，程序是否能适当地接收输入数据而产生正确的输出信息。

黑盒测试着眼于程序外部结构，不考虑内部逻辑结构，主要针对软件界面和软件功能进行测试。

黑盒测试是以用户的角度，从输入数据与输出数据的对应关系出发进行测试的。很明显，如果外部特性本身设计有问题或规格说明的规定有误，用黑盒测试方法是发现不了的。

黑盒测试——等价类划分法
等价类划分法把程序的输入域划分成若干个互不相交的子集，使之为等价类。所谓等价类，是指输入域的某个子集合，所有等价类的并集便是整个输入域。
具有完备性和无冗余性

					有效等价类：相对于该软件规格或需求而言，有意义的，正确的输入。

			       无效等价类：相对于该软件规格或需求而言，无意义的，错误的输入

1：	**按区间划分**：一般分为两个无效区间，一个有效区间
							两个无效区间  ： 小于定义的输入域，大于定义的输入域
							一个有效区间 ：  在定义的输入域范围内

						如定义    0=1

2：   **按数值划分** ：一个有效区间，一个无效区间
   					
   							有效区间 ：  在定义的输入域范围内
							无效区间  ： 不在定义的输入域范围内	

					如定义     交通信号颜色   红黄绿
							有效区间     红灯，黄灯，绿灯
							无效区间    其他颜色的灯，如白灯，橙灯。。。。

3： 按数值集合划分： 和按数值划分类似，不过输入的是一个集合
4： 按限制条件或规划划分：
有效区间 ： 符合输入限制
无效区间 ： 不符合输入限制
5： 细分等价类
等价类中的各个元素在程序中的处理各不相同，则可将此等价类进一步分成更小的等价类

等价类测试的分类
根据等价类的覆盖范围分
弱组合形式：测试用例仅满足对有效等价类的完全覆盖
强组合形式：测试用例不仅满足有效等价类的完全覆盖，也覆盖所有等价类的组合
根据是否对无效数据进行检测分
一般等价类测试：只考虑有效等价类。
健壮等价类测试：考虑有效，无效等价类。

将以上两种组合
弱一般等价类
“一般”表示只考虑有效等价类，“弱”表示测试用例只需覆盖两个输入的所有的有效等价类即可，不需要考虑组合
强一般等价类
“一般”表示只考虑有效等价类，“强”表示测试用例需覆盖两个输入的所有的有效等价类和组合。

			弱健壮等价类
						“”健壮”不仅考虑有效等价类，也考虑无效等价类，“弱”表示测试用例只需覆盖两个输入的所有的有效等价类即可，不需要考虑组合
			强健壮等价类**
					“”健壮”不仅考虑有效等价类，也考虑无效等价类，

等价类设计测试用例的方法
1：划分等价类，形成等价类表，为每一个等价类规定一个唯一的编号。
2：设计一个新的测试用例，使它能够尽量覆盖尚未覆盖的有效等价类3。重复这个步骤，直到所有的有效等价类均被测试用例所覆盖。
3：设计一个新的测试用例，使它能够仅覆盖一个尚未覆盖的无效等价类。重复这个步骤，直到所有的无效等价类均被测试用例所覆盖。

**保险计算问题的等价类测试**
1：分析程序规格说明中给出和隐含的对输入条件的要求
2：列出等价类表
3：设计测试用咧

一次测试最多包含一个无效等价类

边界值方法
边界条件
测试临近边界的合法数据，即测试最后一个可能的合法的数据，以及刚超过边界的非法数据。

										第一个/最后一个，最小值/最大值，开始/完成，超过/在内，空/满，最短/最长，最快/最慢，最早/最迟，最高/最低，相邻/最远
				比最小值略小，最小值，比最小值略大，正常值，比最大值略小，最大值，比最大值略大
				次边界条件

	优点：渐变一下午，生成测试数据的成本很低
	局限性：不能发现测试变量之间的依赖关系，不考虑含义和性质等局限性，因此只能作为初步测试用例使用。

决策表

			决策表方法又叫判定表
			决策表的四个部分
							条件桩（就是条件）：列出了问题的所有条件，除了某些问题对条件的先后次序有特定要求外，通常在这里列出的条件去先后次序无关紧要。
							条件项：针对条件桩给出的条件列出所有可能的取值
							动作桩（就是做法）：给出了问题规定的可能采取的操作，这些操作的排列顺序一般没有什么约束，但为了便于阅读也可令其按适当的顺序排列
							动作项：和条件项紧密相关，指出在条件项的各组取值情况下应采取的动作

把任何一个条件组合的特定取值及相应要执行的动作称为一条规则
在决策表中贯穿条件项和动作项的一列就是一条规则。
显然，决策表中列出多少组条件取值，就有多少条规则
决策表的简化

					以合并相似规则为目标
					若表中有两条或多条规则具有相同的动作，并且在条件项之间存在着极为相似的关系，便可以设法将其合并
					“ —— ”表示与取值无关

规则个数=（取值个数）的输入条件个数次方
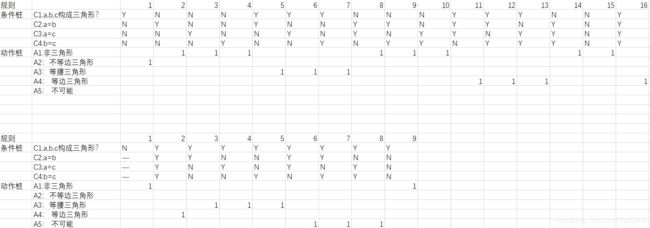
例：

		条件桩
					C1：a,b,c构成三角形
					C2：a=b?
					C3:  a=c?
					C4:  c=b?
		动作桩
				A1:非三角形
				A2：不等边三角形 （笔者感觉应该改成普通三角形）
				A3 ：等腰三角形
				A4：不可能

正交表方法

	正交表具有“均衡分散”和“整齐可比”的特性。利用正交实验设计法进行测试用例设计，从大量的实验数据中心挑选适量的，有代表性的点，从而合理的安排测试的一种科学的实验设计方法
	**正交表的概念和特性**
					
					正交表是一个二维数字表格，其形式为：
																								因子数			
																		L          （水平数           ）
																			行数

· 式中L表示正交表
行数：正交表的行数
因子数：正交表最多可安排的因子数，即正交表列数，它直接对应到用这种技术设计测试用例时变量的最大个数
水平数：每个因子的水平数，任何单个因素能够取得的值的最大个数。它直接对应到用这种技术设计测试用例时，每个变量可能取值的个数。正交表中包含的值为从“0”到“水平数 减去 1”

			构造要因表
						要因表:与一个特定功能相关，由对该功能的结果有影响的所有因素及其状态值构造而成的一个表格
							注意以下几点
									1	：一个要因表只有一个功能相关，多个功能拆分成不同的要因表。
									2   ：要因是指对结果输出有影响的所有因素
									3	：要因的状态值是指要因得可能取值