leetcode45. Jump Game II&&55. Jump Game

Jump Game

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

解决

max记录当前i位置能到达最远距离，其实就是相当于比较"i+nums[i]"在数组nums[i]中水最大，并且比较的前提是，下标i要比记录下最大值要小。

public boolean canJump(int[] A) {
    int max = 0;
    for(int i=0;imax) {return false;}
        max = Math.max(A[i]+i,max);
    }
    return true;
}

Jump Game||

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例: 
输入: [2,3,1,1,4] 
输出: 2 
解释: 跳到最后一个位置的最小跳跃数是 2。 
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明: 
假设你总是可以到达数组的最后一个位置。

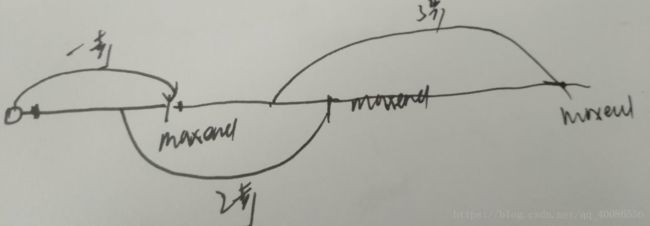
This problem has a nice BFS structure. Let's illustrate it using the example nums = [2, 3, 1, 1, 4] in the problem statement. We are initially at position 0. Then we can move at most nums[0] steps from it. So, after one move, we may reach nums[1] = 3 or nums[2] = 1. So these nodes are reachable in 1 move. From these nodes, we can further move to nums[3] = 1 and nums[4] = 4. Now you can see that the target nums[4] = 4 is reachable in 2 moves.

 

Putting these into codes, we keep two pointers start and end that record the current range of the starting nodes. Each time after we make a move, update startto be end + 1 and end to be the farthest index that can be reached in 1 move from the current [start, end].

 

To get an accepted solution, it is important to handle all the edge cases. And the following codes handle all of them in a unified way without using the unclean ifstatements :-)

 

---

    public int jump(int[] nums) {
        if (nums.length <= 1) return 0;
        int curMax = 0; // to mark the last element in a level
        int level = 0, i = 0;
        while (i <= curMax) { 
            int furthest = curMax; // to mark the last element in the next level
            for (; i <= curMax; i++) {
                furthest = Math.max(furthest, nums[i] + i);
                if (furthest >= nums.length - 1) return level + 1;
            }
            level++;
            curMax = furthest;
        }
        return -1; // if i < curMax, i can't move forward anymore (the last element in the array can't be reached)
    }

C++

动态规划解法： 
复杂度是 O(n2)O(n2)，会超时，但是依然需要掌握。

定义状态：dp[i] 表示到达 i 位置的最小跳数 
起始装填：dp[0]=0 到达下标0的最小跳数是0 
终止状态：dp[nums.length-1] 即到达最后一个位置的最小跳数 
决策：选择 i 之前的能跳到 i 的所有位置j 中， dp[j] 值最小的位置 j 作为上一步要跳到 i 的位置 
费用表示：dp[i]=dp[j]+1 ,从 j 跳到 i ,步数加1 
无后效性：收益1 是个常数，不随状态改变

class Solution {
    public int jump(int[] nums) {
        int[] dp = new int[nums.length];//dp[i] 为到达 i 位置的最小跳数
        dp[0] = 0;//到达下标0的最小跳数是0
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Integer.MAX_VALUE;
            for (int j = 0; j < i; j++) {
                if (i - j <= nums[j]) {
                    dp[i] = Math.min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[nums.length - 1];
    }
}