深度学习简介与MLP多层感知机
研究更复杂的深度学习方法的起点为MLP,即用于分类和回归的多层感知机,MLP也被称为普通前馈神经网络或者简称为神经网络。
神经网络模型基础介绍
MLP可以被看做是广义的线性模式,只是执行了多层后才得到结论。
线性模型的回归公式:
y = w[0] * x[0] + w[1] * x[1] + ...+...+b
上面的公式可以看出,y是输入特征x[0]到x[p]的加权求和,权重为模型学习到的系数w。
我们可以对比下简单的线性模型和多层的神经网络:
display(mglearn.plots.plot_logistic_regression_graph())
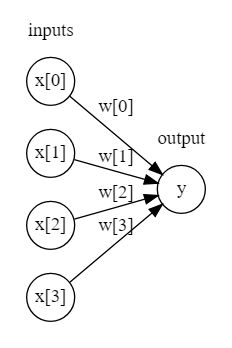
左边的节点代表输入的特征,中间的连线代表学习到的系数,右边的y代表输出的结果,即加权求和的结果。
我们再看看单隐层的多层感知机:
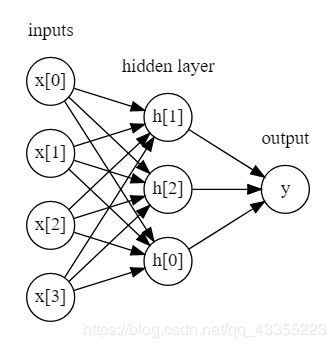
每个输入的特征与隐单元之间有一个系数,每一个隐单元与输出的结果之间也有一个系数,这些系数可以称之为权重,这些隐单元也组成了一个隐层,上图是一个单隐层的神经网络模型。
这里会有一个问题,因为计算一系列多层的加权求和和只计算一次加权求和是完全一样的。那么这个神经网络模型和普通的线性模型到底有什么不同呢?
对每个隐单元的结果再套上一个非线性函数:这个非线性函数通常是校正非线性 relu和正切双曲线 tanh。然后再对经过非线性函数计算过的隐单元结果进行加权求和,就得到了最终的结果y。
所以以一个小型神经网络为例子:计算回归问题的y的实际公式其实是
h[0] = w0*x[0] + w1*x[1] +...+ wp*x[p] + b[0]
h[1] = w0*x[0] + w1*x[1] +...+ wp*x[p] + b[1]
h[2] = w0*x[0] + w1*x[1] +...+ wp*x[p] + b[2]
y = v0*h[0] + v1*h[1] + v2*h[2] + b
对于神经网络而言,有一个重要的参数是隐层中隐单元的个数。对于非常简单的数据集而言,隐单元的个数可以是10个,对于非常复杂的数据集,隐单元的个数可以大到10000。并且还可以添加多个隐层。所以这样多个计算层构成的大型神经网络,可以说是和深度学习这个词非常的搭配了。
研究MLP(多层感知机)的工作原理,调参
我们使用MLPClassifier应用到数据集上来研究原理:
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,random_state=42)
mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

根据上图我们可以看到神经网络的决策边界是非线性的,但是相对平滑,默认情况下,MLP使用100个隐节点,可以减少,那就降低了模型的复杂度。MLP还默认使用relu。
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10])
当我们使用10个隐单元,1个隐层的时候,决策边界将由10个直线段组成。如果我们想要更平滑的决策边界,我们可以使用更多隐单元,隐层,或者使用tanh非线性函数。
**使用2个隐层,每层10个隐单元:**修改hidden_layer_sizes属性
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10])
**使用tanh非线性函数:**修改activation属性
mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=[10, 10])
使用L2正则化: 修改alpha参数:
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes], alpha=0.0001)
我们可以使用L2正则化使权重更加趋向于0,MLP中控制L2惩罚系数的参数是alpha,alpha值越小,就越是弱正则化,决策边界越平滑
对于MLP以及深度学习的评价:
虽然MLP为最常见的神经网络架构提供了易于使用的接口,但是MLP只包含神经网络潜在应用的一部分,对于深度学习,推荐使用sklearn之外的库,目前最为完善的是keras, tensor-flow,两者的关系是:TensorFlow,theano,Keras都是深度学习框架,TensorFlow和theano比较灵活,也比较难学,它们其实就是一个微分器。Keras其实就是TensorFlow和keras的接口(Keras作为前端,TensorFlow或theano作为后端),所以,Keras可以看做是TensorFlow封装好的API推荐使用tf里面的tf.keras模块,两者无缝集成
所有好得流行的深度学习框架一般都支持GPU,但是sklearn不支持GPU,然而使用GPU运算速度的提升至少在10倍以上。
神经网络目前是最先进的机器学习模型,可以构建无比复杂的模型,在给定足够的时间下,调节参数,神经网络一般可以打败任何其他机器学习算法。