K 凸函数的一些性质和相关证明

一、K 凸函数的定义：

定义1 $\forall a,b>0$
$$K+f(a+x)-f(x)-a\left\{\frac{f(x)-f(x-b)}{b}\right\}\ge 0$$
定义2$\forall a>0$
$$K+f(a+x)-f(x)-a{f}^{\prime }(x)\ge 0$$
定义3$\forall 0<\mu <1$
$$\mu f(x_1)+(1-\mu )(f(x_2)+K)\ge f(\mu x_1+(1-\mu )x_2)$$

定义3 其实由定义1 改造而来，只要令 $x_1=x-b$, $x_2=x+a$, $\mu =\frac{a}{a+b}$ 即可。

还有一个 CK 凸函数，它针对能力约束问题，此时， $0<a\le C$, $0<b\le C$。

二、一个 K 凸函数图像：

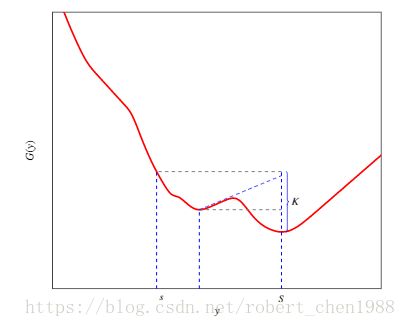
K 凸的几何意义是：对于三个点 $x-b$, $x$, $x+a$，$(x-b,f(x-b))$, $(x,f(x))$ 的连线在 $x+a$ 的值一定落在$f(x+a)+K$ 下面。

三、$s$, $S$ 的定义

设 $f$ 为在定义域 $[A,B]$ 上的一个 K 凸函数，$f^{\ast }$ 为其在定义域内的最小值，

$$\begin{array}{rl}S& =\{x\mid f(x)=f^{\ast }\}\\ s& =\min \{x\mid f(x)\le f^{\ast }+K,x\le B\}\end{array}$$
注：$s$ 可能不在定义域内。

四、K-凸函数的相关性质

1. $f(x)$ 在区间 $[A,s]$ 上单调递减.

证明：当 $x<s$ 时，根据 $s$ 的定义，显然 $f(x)>f(S)+K$。令 $x+a=S$，则根据定义1 或定义 2，当 $x<s$ 时,
$$a{f}^{\prime }(x)\le K+f(S)-f(x)<0$$
因此 $f(x)$ 在区间 $[A,s]$ 上单调递减。

2. 对任意 $s<x_1<x_2$，都有 $f(x_2)+K\ge f(x_1)$.

证明：
(1) 若 $x_2>x_1\ge S$ 或 $x_1<x_2\le S$, 在定义1 中令 $x-b=S$, $x+a=x_2$, $x=x_1$，得到：
$$\begin{array}{rl}& K+f(x_2)-f(x_1)-(x_2-x_1)\left\{\frac{f(x_1)-f(S)}{x_1-S}\right\}\ge 0\\ \Rightarrow & K+f(x_2)-f(x_1)\ge (x_2-x_1)\left\{\frac{f(x_1)-f(S)}{x_1-S}\right\}\\ \Rightarrow & K+f(x_2)-f(x_1)\ge 0(\text{since}f(x_1)\ge f(S))\end{array}$$
(2) 若 $x_1<S<x_2$，在定义1 中令 $x+a=S$, $x-b=s$, $x=x_1$，得到：
$$\begin{array}{rl}& K+f(S)-f(x_1)-(S-x_1)\left\{\frac{f(x_1)-f(s)}{x_1-s}\right\}\ge 0\\ \Rightarrow & K+f(S)-f(x_1)\ge (S-x_1)\left\{\frac{f(x_1)-f(S)-K}{x_1-s}\right\}\\ \Rightarrow & K+f(S)-f(x_1)\ge 0\Rightarrow K+f(x_2)-f(x_1)\ge 0(\text{since}f(x_2)\ge f(S))\end{array}$$$\square$

对任意 $s<x_1<x_2$，当然也满足 K-凸条件：$K+f(x_2)\ge f(x_1)+(x_2-x_1)\frac{f(x_1)-f(x_1-b)}{b}$

3. 在定义域 $[A,B]$ 上的最优订货策略为 $(s,S)$, 即：

$$\begin{array}{rl}g(x)=& \underset{y\ge x,A\le y\le B}{\inf }[K\delta (y-x)+f(y)]\\ =& \{\begin{array}{ll}f(S)+K& x<s\\ f(x)& x\ge s\end{array}\end{array}$$

需要证明 当 $f(x)$ 为 k 凸函数时，$g(x)$ 为 k 凸函数。
证明：我们需证明 $g(x)$ 满足定义1. 对任意三个点 $x-b$, $x$, $x+a$
一共有以下四种情况：
(1) 若 $x-b\ge s$ 时，
$$\begin{array}{rl}& K+g(x+a)-g(x)-a\left\{\frac{g(x)-g(x-b)}{b}\right\}\\ =& K+f(x+a)-f(x)-a\left\{\frac{g(x)-g(x-b)}{b}\right\}\end{array}$$
上式就是 $f(x)$ K凸函数的定义，显然成立。

(2) 若 $x+a<s$ 时，
$$\begin{array}{rl}& K+g(x+a)-g(x)-a\left\{\frac{g(x)-g(x-b)}{b}\right\}\\ =& K+f(S)+K-f(S)-K-a\left\{\frac{f(S)+K-f(S)-K}{b}\right\}\\ =& 0\end{array}$$
上式显然是 K凸函数。

(3) 若 $x-b<x<s<x+a$ 时，
$$\begin{array}{rl}& K+g(x+a)-g(x)-a\left\{\frac{g(x)-g(x-b)}{b}\right\}\\ =& K+f(x+a)-f(S)-K-a\left\{\frac{f(S)+K-f(S)-K}{b}\right\}\\ =& f(x+a)-f(S)\ge 0\end{array}$$
为 K凸函数。

(4) 若 $x-b<s<x$ 时，
$$\begin{array}{rl}& K+g(x+a)-g(x)-a\left\{\frac{g(x)-g(x-b)}{b}\right\}\\ =& K+f(x+a)-f(x)-a\left\{\frac{f(x)-f(S)-K}{b}\right\}\\ \ge & K+f(x+a)-f(x)-a\left\{\frac{f(x)-f(s)}{b}\right\}\end{array}$$

根据性质2， $K+f(x+a)-f(x)\ge 0$。
若 $f(x)\le f(s)$，上式显然大于等于零。
若 $f(x)<f(s)$，根据性质 1，可以得出 $x>s$，又因为 $x-b<s$，即 $b>x-s$，上述表达式可以变为：
$$\begin{array}{rl}& K+f(x+a)-f(x)-a\left\{\frac{f(x)-f(s)}{b}\right\}\\ \ge & K+f(x+a)-f(x)-a\left\{\frac{f(x)-f(s)}{x-s}\right\}\end{array}$$

刚好为 K凸函数的定义，因此也大于等于零。

综合以上，在四种情况下，$g(x)$ 均为 K 凸函数。$\square$

4. 若 $g$ 为一个 K-凸函数，则 $f$ 也是一个 K-凸函数，其中 $f$ 为

$$f(x)=\underset{x\le y\le x+R}{\min }g(y)$$

证明：
我们需要证明
$$f(\mu x_1+(1-\mu )x_2)\le \mu f(x_1)+(1-\mu )(f(x_2)+K)$$

设 $f(x)=g(x+\beta (x)R)$，其中 $\beta (x)\in [0,1]$，则
$$\begin{array}{rl}& \underset{0\le z\le R}{\min }g(\mu x_1+(1-\mu )x_2+z)\\ & \le g(\mu x_1+(1-\mu )x_2+\mu \beta (x_1)R+(1-\mu )\beta (x_2)R)\end{array}$$

上面这一步很巧， 利用构造函数去掉了 min 对分析函数性质的影响，也最重要，下面使用时结合了 $f(x)$ 的定义（第一个小于等于号，稍微有点绕）

因此
$$\begin{array}{rl}f(\mu x_1+(1-\mu )x_2)& =g(\mu x_1+(1-\mu )x_2+\beta (\mu x_1+(1-\mu )x_2)R)\\ & \le g(\mu x_1+(1-\mu )x_2+\mu \beta (x_1)R+(1-\mu )\beta (x_2)R)\\ & =g(\mu (x_1+\beta (x_1)R)+(1-\mu )(x_2+\beta (x_2)R))\\ & \le \mu g(x_1+\beta (x_1)R)+(1-\mu )(g(x_2+\beta (x_2)R)+K))\\ & =\mu f(x_1)+(1-\mu )(f(x_2)+K)\end{array}$$
得证 $\square$