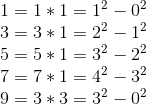数论 —— 整数分解

【概述】

整数分解目前仍是世界级难题，是非常重要的研究方向，其有很多种算法，性能上各有差异，本文仅介绍试除法、Fermat 算法、Pollard Rho 算法。

【试除法】

试除法也叫穷举法，是整数分解算法中最简单和最容易理解的算法，但也是效率最低的算法。

试除法是用小于等于 n 的每个素数去试除待分解的整数，如果找到一个数能够整除除尽，这个数就是待分解整数的因子。

试除法一定能够找到 n 的因子，因为它检查 n 的所有可能的因子，所以如果这个算法失败，也就证明了 n 是个素数，因此，试除法也常用来判断一个数是不是质数。

bool judge(int n)
{
    if(n==1)//1不是一个有效因数
        return false;

    for(int i=2;i

【Fermat 算法】

Fermat 算法分解大数的效率并不高，但比起试除法要好了很多，且每次计算都是计算出 N 的一个因子，更降低了其效率。

1.费马整数分解

对于一个任意的偶数，我们都可以通过不断提出为 2 的质因子使其最终简化为一个 2 的 n 次幂与一个奇数，因此，任意一个奇数都可以表示为：N=2*n+1

若这个奇数 N 是一个合数，根据唯一分解定理，其一定可以写成 N=c*d 的形式，不难发现，式中 c、d 均为奇数

设：c>d，令 a=(c+d)/2，b=(c-d)/2

可得：N=c*d=a*a-b*b

例如：

2.费马因式分解算法

由于 

因此 

即：

因此，我们可以从  开始枚举，计算  为完全平方数即可求出 a、b，从而可以求得：c=a+b，d=a-b(a>b)

int res[N];
void Fermat(int n)
{
    int a,b,temp;

    a=sqrt(n);
    if(a*a

【Pollard Rho 算法】

为进一步提高效率，解决因数太多无法存储的问题，我们有了 Pollard Rho 算法。

1.算法原理

其原理已知待分解的大整数 n，再通过某种方法得到两个整数 a、b，计算 ，直到 p不为1，或 a、b 出现循环为止，然后再判断 p 的值，若 p=n 或 p=1，那么返回的 n 是一个质数，否则返回的 p 是 n 的一个因子，因此我们可以递归的计算 Pollard(p) 与 Pollard(n/p) ，从而求出 n 所有的因子。

实际操作中，我们通常使用函数： 来不断生成伪随机数，用于逐步迭代计算 a、b 的值。

实践中，常取 c=1，再任意取两初值 a、b，即：，在下一次计算中，将 b 的值赋给 a，再次使用上式来计算新的 b 的值，直至 a、b 出现循环。

但是这样判断 a、b 的循环十分麻烦，例如生成伪随机数为：2，10，16，23，29，13，16，23，29，13...时，很难判断循环，因此我们可以采用 Floyd 判环算法来判断循环。

2.Floyd 判环算法实现Pollard Rho 算法

利用多项式 f(x) 迭代出 的值，然后设定 x、y 的初值，选用多项式进行迭代

每次令：，即：

当 x=y 时即出现循环

int GCD(int a,int b)
{
    return b?GCD(b,a%b):a;
}

int Pow_Mod(int a, int b, int m)
{
    int res=1;
    while(b)
    {
        if(b&1)
            res=(res*a)%m;
        a=(a*a)%m;
        b>>=1;
    }
}

long long pollard_rho(long long x, long long c)//寻找一个因子
{
    long long i=1,k=2;
    srand(time(NULL));
    long long x0=rand()%(x-1)+1;//产生随机数x0(并控制其范围在1 ~ x-1之间)
    long long y=x0;
    while(1)
    {
        i++;
        x0=(Pow_Mod(x0,x0,x)+c)%x;
        long long gcd=GCD(y-x0,x);

        if(gcd!=1&&gcd!= x)
            return gcd;

        if(y==x0) 
            return x;

        if(i==k)
        {
            y=x0;
            k+=k;
        }
    }
}

3.存储大整数的所有因子

组合使用 Pollard Rho 算法与 Miller Rabin 算法，可求出大整数的所有因子。

LL Mult_Mod(LL a,LL b,LL m)//res=(a*b)%m
{
    a%=m;
    b%=m;
    LL res=0;
    while(b)
    {
        if(b&1)
            res=(res+a)%m;
        a=(a<<=1)%m;
        b>>=1;
    }
    return res%m;
}
LL Pow_Mod(LL a, LL b, LL m)//res=(a^b)%m
{
    LL res=1;
    LL k=a;
    while(b)
    {
        if((b&1))
            res=Mult_Mod(res,k,m)%m;

        k=Mult_Mod(k,k,m)%m;
        b>>=1;
    }
    return res%m;
}

bool Witness(LL a,LL n,LL x,LL sum)
{
    LL judge=Pow_Mod(a,x,n);
    if(judge==n-1||judge==1)
        return 1;

    while(sum--)
    {
        judge=Mult_Mod(judge,judge,n);
        if(judge==n-1)
            return 1;
    }
    return 0;
}

bool Miller_Rabin(LL n)
{
    if(n<2)
        return 0;
    if(n==2)
        return 1;
    if((n&1)==0)
        return 0;

    LL x=n-1;
    LL sum=0;
    while(x%2==0)
    {
        x>>=1;
        sum++;
    }


    int times=20;
    for(LL i=1;i<=times;i++)
    {
        LL a=rand()%(n-1)+1;//取与p互质的整数a
        if(!Witness(a,n,x,sum))//费马小定理的随机数检验
            return 0;
    }
    return 1;
}
LL GCD(LL a,LL b)
{
    return b==0?a:GCD(b,a%b);
}
LL Pollard_Rho(LL n,LL c)//寻找一个因子
{
    LL i=1,k=2;
    LL x=rand()%n;//产生随机数x0(并控制其范围在1 ~ x-1之间)
    LL y=x;
    while(1)
    {
        i++;
        x=(Mult_Mod(x,x,n)+c)%n;
        LL gcd=GCD(y-x,n);

        if(gcd<0)
            gcd=-gcd;

        if(gcd>1&&gcd=n)//值变化，防止陷入死循环k
        p=Pollard_Rho(p,rand()%(n-1)+1);

    Find_fac(n/p);
    Find_fac(p);
}

【例题】 

• Prime Test（POJ-1811）(Pollard Rho 与 Miller Rabin 求大整数分解)：点击这里