关于字符串的算法题2:最长公共前缀,最长回文子串
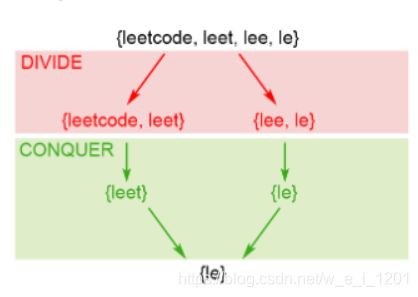
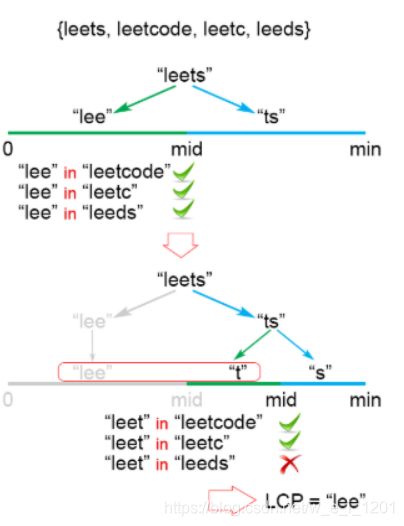
1. 最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 “”。
示例 1:
输入: [“flower”,“flow”,“flight”]
输出: “fl”
示例 2:
输入: [“dog”,“racecar”,“car”]
输出: “”
解释: 输入不存在公共前缀。
说明:
所有输入只包含小写字母 a-z 。
java答案:
1. 首先先进行前两个选择,找到公共前缀,再和第三个比,知道有空字符串或公共前缀为null时停止。
1.1. class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs.length==0){
return "";
}
if(strs.length==1){
return strs[0];
}
char[] str1 = strs[0].toCharArray();
char[] str2;
int length = str1.length;
for(int i=0;i class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
return longest(strs,0,strs.length-1);
}
public String longest(String[] strs,int left,int right){
if(left==right){
return strs[left];
}
int mid=(left+right)/2;
String l = longest(strs,left,mid);
String r = longest(strs,mid+1,right);
return common(l,r);
}
public String common(String l,String r){
if(l=="" || r==""){
return "";
}
int length = Math.min(l.length(),r.length());
for(int i=0;iclass Solution {
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
if(strs.length==0) return strs[0];
int minLen = Integer.MAX_VALUE;
for(int i=0;i注意:
- startsWith() 方法用于检测字符串是否以指定的前缀开始。
public boolean startsWith(String prefix, int Index)或public boolean startsWith(String prefix)
prefix是前缀,Index是字符串中开始查找的位置。 - public int indexOf(int ch): 返回指定字符在字符串中第一次出现处的索引,如果此字符串中没有这样的字符,则返回 -1。
public int indexOf(int ch, int fromIndex): 返回从 fromIndex 位置开始查找指定字符在字符串中第一次出现处的索引,如果此字符串中没有这样的字符,则返回 -1。
int indexOf(String str): 返回指定字符在字符串中第一次出现处的索引,如果此字符串中没有这样的字符,则返回 -1。
int indexOf(String str, int fromIndex): 返回从 fromIndex 位置开始查找指定字符在字符串中第一次出现处的索引,如果此字符串中没有这样的字符,则返回 -1。
JavaScript答案:
1.
/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function(strs) {
if (strs.length == 0) return "";
var prefix = strs[0];
for (var i = 1; i < strs.length; i++)
while (strs[i].indexOf(prefix) != 0) {
prefix = prefix.substring(0, prefix.length - 1);
if (prefix=="") return "";
}
return prefix;
};
6.
var longestCommonPrefix = function(strs) {
if (strs.length == 0) return "";
for(var i=0;i2. 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
示例 2:
输入: “cbbd”
输出: “bb”
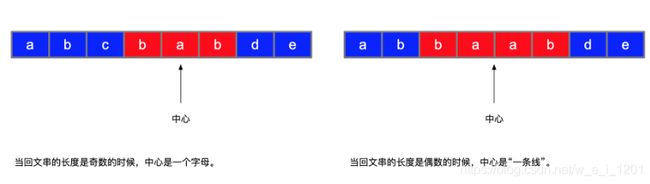
1. 中心扩散法:遍历每个索引,以这个索引为中心,往两边扩散,记录最长的子串。这个回文子串有可能是偶数,有何能是奇数。
如果传入重合的索引编码,就是奇数,如果传入相邻的索引编码就是偶数。
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len == 0) {
return "";
}
int longestLen = 1;
String longestStr = s.substring(0, 1);
for (int i = 0; i < len; i++) {
String palindromeOdd = centerSpread(s, len, i, i); //奇数时,中心传入了两次这个数
String palindromeEven = centerSpread(s, len, i, i + 1); //偶数时,中心是这个数和下一个数
String maxLen = palindromeOdd.length() > palindromeEven.length() ? palindromeOdd : palindromeEven;
if (maxLen.length() > longestLen) {
longestLen = maxLen.length();
longestStr = maxLen;
}
}
return longestStr;
}
private String centerSpread(String s, int len, int left, int right) {
int l = left;
int r = right;
while (l >= 0 && r < len && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 这里要特别小心,跳出 while 循环的时候,是第 1 个满足 s.charAt(l) != s.charAt(r) 的时候
// 所以,不能取 l,不能取 r
return s.substring(l + 1, r);
}
}
时间复杂度是o(n^2),空间复杂度是o(1).
2. 动态规划:给出一个布尔矩阵,如果 dp[l, r] = true 那么 dp[l + 1, r - 1] 也一定为 true,矩阵使用的放下是先从上往下,再从左往右,
// abcdedcba
// l r
// 如果 dp[l, r] = true 那么 dp[l + 1, r - 1] 也一定为 true
// 关键在这里:[l + 1, r - 1] 一定至少有 2 个元素才有判断的必要
// 因为如果 [l + 1, r - 1] 只有一个元素,不用判断,一定是回文串
// 如果 [l + 1, r - 1] 表示的区间为空,不用判断,也一定是回文串
// [l + 1, r - 1] 一定至少有 2 个元素 等价于 l + 1 < r - 1,即 r - l > 2
// 写代码的时候这样写:如果 [l + 1, r - 1] 的元素小于等于 1 个,即 r - l <= 2 ,就不用做判断了
// 因为只有 1 个字符的情况在最开始做了判断
// 左边界一定要比右边界小,因此右边界从 1 开始
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if(len<=1 || s.equals(" ")){
return s;
}
int longestlen = 1;
String longestStr = s.substring(0, 1);
boolean[][] dp = new boolean[len][len];
for (int r = 1; r < len; r++) {
for (int l = 0; l < r; l++) {
// 区间应该慢慢放大
// 状态转移方程:如果头尾字符相等并且中间也是回文
// 在头尾字符相等的前提下,如果收缩以后不构成区间(最多只有 1 个元素),直接返回 True 即可
// 否则要继续看收缩以后的区间的回文性
// 重点理解 or 的短路性质在这里的作用
if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
dp[l][r] = true;
if (r - l + 1 > longestlen) {
longestlen = r - l + 1;
longestStr = s.substring(l, r + 1);
}
}
}
}
return longestStr;
}
}
时间复杂度是o(n^2),空间复杂度是o(n^2),因为使用了一个二维矩阵。
3. 暴力解法
class Solution {
public String longestPalindrome(String s) {
if(s.length() <= 1){
return s;
}
for(int i=s.length();i>0;i--){ //决定子串长度
for(int j=0;j<=s.length()-i;j++){
String sub = s.substring(j,j+i); //截取子串
int count=0; //用来判断是否对称
for(int k=0;kJavaScript答案:
1. 中心扩散法
/**
* @param {string} s
* @return {string}
*/
var longest = function(s,len,l,r){
while(l>=0 && revent.length?odd.length:event.length;
if(max>longestLen){
longestLen = max;
longestStr = odd.length>event.length?odd:event;
}
}
return longestStr;
};
2. 动态规划
var longestPalindrome = function(s) {
if(s.length<=1 || s==""){
return s;
}
var len = s.length;
var dp = new Array(len);
for(var i=0;ilongestLen){
longestLen =r-l+1;
longestStr = s.substring(l,r+1);
}
}
}
}
return longestStr;
};