桃桃七泡惹

2020宁波市多校赛训练biu~

宁波市多校训题整理-未完待续...

一、宁波市多校训练（一）

A - 或异或或异或或异或

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

B - 狂赌之渊

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

E - ddd的逛街计划(Easy Version)

题目描述
Input
Output
Sample Input
Sample Output
理解
AC代码

H - 小w的半阶乘平方

题目描述
Input
Output
Sample Input
Sample Output
理解
AC代码

二、宁波市多校训练（二）

C - 树行棋

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

D - LCA！

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

E - 最大限定倍数(Easy Version)

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

F - 最大限定倍数(Normal Version)

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

H - 棋盘(Easy Version)

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

三、宁波市多校训练（三）

A - C语言头文件识别器

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

B - 小w和小doge的互质数(Easy Version)

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

D - 礼物分配问题(Easy Version)

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

题目描述
Input
Output
Sample Input
Sample Output
Hint
理解
AC代码

四、宁波市多校训练（四）

A - 炉石传说——按费拍怪是王道

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

C - 石头划分

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

D - 树上的点到链

题目描述
Input
Output
Sample Input
Sample Output
AC代码

E - 相同的地板

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

G - 隐秘的峡谷

题目描述
Input
Output
Sample Input
Sample Output
AC代码

五、宁波市多校训练（五）

A - 龙珠

题目描述
Input
Output
Sample Input
Sample Output
AC代码

B - 少抢了多少红包

题目描述
Input
Output
Sample Input
Sample Output
AC代码

D - 小伙子找姑娘

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

六、宁波市多校训练（六）

C - 分享蛋糕（Easy）

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

F - 天天天天想女装

题目描述
Input
Output
Sample Input
Sample Output
AC代码

G - 猩球崛起

题目描述
Input
Output
Sample Input
Sample Output
Hint
AC代码

未完待续...

一、宁波市多校训练（一）

A - 或异或或异或或异或

题目描述

给你N个数，要你求出从a1以1递增的异或到a2，以1递增的或到a3，以1递增的异或到a4，以1递增的或到a5，以1递增的异或到a6以此类推（或与异或交替进行）一直到an，举个例子 n=5，a1=2,a2=3,a3=9,a4=13,a5=15则我们要求的东西就是2 ^ 3 | 4 | 5 | 6 | 7 | 8 | 9 ^ 10 ^ 11 ^ 12 ^ 13 | 14 | 15.(忽略位运算符的运算优先级，从左至右依次进行计算)

Input

第一行输入一个T表示T组案例（T≤400），每组案例输入一个整数n，1≤n≤5000,然后n个数每个数小于10^100，我们保证给你的这n个数是递增的正整数。

Output

输出结果

Sample Input

1
5
2 3 9 13 15

Sample Output

Hint

当数据范围小于1e4时大家可以用这段程序求解，但是本题数据范围远大于1e4，这段程序仅帮助大家理解题意和用这段程序来寻找规律，祝大家都能ac

#include
int a[5200];
int main() {
   int t;
   scanf("%d",&t);
   while(t--){
      int n;
      scanf("%d",&n);
      for(int i=0; i<n; i++)
         scanf("%d",&a[i]);
      int sum=a[0];
      int flag=0;
      int cnt=1;
      for(int i=a[0]+1; i<=a[n-1]; i++)
      {
         if(flag%2==0)
         {
            sum^=i;
         }
         else
         {
            sum|=i;
         }
         if(a[cnt]==i)
         {
            flag++;
            cnt++;
         }

      }  printf("%d\n",sum);
   }
}

AC代码

def cal1(n):
    tt = n & 3
    if (tt&1) :
        return (tt // 2) ^ 1
    else:
        return (tt // 2) ^ n

def cal2(n,m):
    cnt = 0
    tt = m - n
    while tt != 0:
        tt //= 2
        cnt += 1
    n |= m
    n |= pow(2,cnt)-1
    return n
cas = int(input())
while cas != 0:
    cas -= 1
    n = int(input())
    l = list(map(int,input().split()))
    ans = cal1(l[1])^cal1(l[0]-1)
    for i in range(2,n):
        if (i&1):
            ans ^= (cal1(l[i])^cal1(l[i-1]))
        else:
            ans |= cal2(l[i - 1] + 1,l[i])
    print(ans)

B - 狂赌之渊

题目描述

有一部动画叫做狂赌之渊，剧中女主角蛇喰梦子与早乙女芽亚里之间进行了一场赌博，方式是双方各从一堆拥有“剪刀”，“石头”，“布”，的牌堆中各抽出三张，牌堆中这三种卡的数量并不一定相同，然后每个人先亮出三张牌中的一张牌，如果被亮出的第一张牌未能决定胜负（两个人亮出了相同的牌），则双方再亮出一张，若第二张无法决定胜负，则亮出第三张，如果三次亮牌都无法决定胜负则算平局。现在蛇喰梦子通过观察早乙女芽亚里的神情知道了她手上的三张牌并且知道了她打出牌的顺序，然后又观察到了准备牌的人铃井凉太的动作知道了牌堆每张牌的数量，问你现在轮到蛇喰梦子抽牌了，问抽到一手能获胜的牌的概率是多少。胜负关系是：剪刀赢布，布赢石头，石头赢剪刀。因为蛇喰梦子知道对手怎么出牌，所以她的出牌顺序一定是最优的

Input

第一行输入一个T(T≤1e3)，表示T组案例，每组案例输入6个数字，A,B,C,X,Y,Z。A,B,C表示早乙女芽亚里抽完之后剪刀石头布各剩下几张，X,Y,Z表示早乙女芽亚里的出牌顺序，0≤A,B,C≤1000;A+B+C≥3;X,Y,Z∈{1,2,3}其中X代表早乙女芽亚里第一张打出的牌是什么，Y代表第二张，Z代表第三张，1代表剪刀，2代表石头，3代表布。输入数据保证合法

Output

在知道早乙女芽亚里的出牌情况之后，蛇喰梦子抽到一手能获胜的牌的概率是多少，结果四舍五入保留两位小数

Sample Input

1
3 1 1
1 1 2

Sample Output

0.90

Hint

案例中：假设我们给5张牌都标个号从：1~5标号，我们5张卡牌中随机抽取3张（不考虑顺序只考虑组合
有10种组合情况分别是（123；124；125；134；135；145；234；235；245；345），每种情况的概率是10%
然后标号为1,2,3的为剪刀；4为石头；5为布。
对手是剪刀剪刀石头，我们只有抽到三个剪刀（123）的时候不能胜利此情况为10%
抽到两个剪刀一个布（125或者135或者235）此情况为30%，可以通过前两轮出剪刀第三轮出布获得胜利。
如果有石头（124；134；145；234；245；345）可以通过第一轮出石头获得胜利此情况为60%
所以抽到能获胜的3张牌的概率是0.3+0.6=0.9

AC代码

#include
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
typedef long long ll;
typedef pair <int,int> PAIR;
const int maxn = 2e5 + 207;
const double pi = acos(-1);
const ll mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
int vis[7];
int a[maxn];
ll sum = 0;
double ans = 0;
void dfs(int st,double num,string s){
	if(st == 3){
		int v2[3];
		memset(v2,0,sizeof(v2));
		for(int i = 0;i < 3;i++){
			int fl = 0;
			int k = 0;
			for(int j = 0;j < 3;j++){
				if((vis[i] + 1 == s[j] - '0' || (vis[i] == 3 && s[j] == '1')) && !v2[j]){
                    fl = 1;
                    break;
                }else if(vis[i] == s[j] - '0' && !v2[j]){
                    fl = 2;
                    k = j;
                }
			}
			if(fl == 2) v2[k] = 1;
            if(fl == 0) break;
            if(fl == 1){
                ans += num;
                break;
            }
		}
		return;
	}
	for(int i = 0;i < 3;i++){
		if(a[i]){
			a[i]--;
			dfs(st+1, num * (a[i]+1)/(sum-st), s+char('1'+i));
            a[i]++;
		}
	}
}
int main(){
	int cas;
	scanf("%d",&cas);
	while(cas--){
		ans = 0;
		sum = 0;
		for(int i = 0;i < 3;i++){
			scanf("%d",&a[i]);
			sum += a[i];
		}
		for(int i = 0;i < 3;i++){
			scanf("%d",&vis[i]);
		}
		dfs(0,1,"");
		printf("%.2lf\n",ans);
	}
	return 0;
}

E - ddd的逛街计划(Easy Version)

题目描述

本题有对应的Hard Version，本题与Hard的区别仅在本题保证L=R
ddd在追学妹，所以他常常陪学妹一次逛街。
ddd最近太忙了, 每天都有课. 这不怕, ddd可以请假不去上课。
学妹是一个乖巧的人，所以如果在任意连续的 k 天中ddd不能够至少陪伴她L天，学妹就会很伤心，偏偏学校又有规定, 任意连续 k 天中, 不得请假超过 R 天，ddd很忧伤, 因为他还要陪学妹去逛街呢.，ddd既不想让学妹伤心，同时又不想违背学校的规定。
后来, ddd发现, 如果自己哪一天智商更高一些, 陪学妹逛街会得到更多的好感度，不过呢，ddd他的智商并不是总是正数，他也有智商下线的时候，所以ddd的智商有正有负。
现在 ddd决定做一个实验来验证自己的猜想, 他拜托张老师预测出了自己未来 n 天中, 每一天的智商.
ddd希望在之后的 n天中选出一些日子来陪学妹逛街, 要求在不违反校规，并且不让学妹伤心的情况下, 陪学妹逛街的日子自己智商的总和最大。
ddd想知道这个最大的和。

Input

第一行输入一个正整数T，表示有T组测试案例。
对于每组测试样例:
首先输入一个正整数n(1≤n≤500)
接下来一行n个整数ai(−1e5≤ai≤1e5)
接下来一行输入三个正整数K,L,R(1≤K≤n,0≤L=R≤K)
注意：由于是easy版本，所以保证输入的L=R

Output

仅一行一个整数，表示ddd智商的最大和

Sample Input

5
5
1 2 3 4 5
3 2 2
7
4 -8 -9 -8 -9 -8 -9
2 1 1
7
4 -8 -9 -8 -9 -8 -9
2 2 2
4
-7 2 8 6
3 2 2
10
-1 -2 -3 -4 -5 -6 -7 -8 -9 -10
1 1 1

Sample Output

12
-23
-47
10
-55

理解

 E作为简单版本，其实就是一个固定长度的滑动窗口选择LR个的话 
LR+x个选与不选的状态与第x个相同，所以开数组桶装一下，第i%L相同的放到一起，然后sort贪心即可

AC代码

#include
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
typedef long long ll;
typedef pair <int,int> PAIR;
const int maxn = 5e5 + 7;
const double pi = acos(-1);
const ll mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
int a[507];

int main(){
    int cas;
	scanf("%d",&cas);
	while(cas--){
		int n;
		scanf("%d",&n);
		for(int i = 0;i < n;i++){
			scanf("%d",&a[i]);
		}
		int k,l,r;
		scanf("%d %d %d",&k,&l,&r);
		for(int i = 0;i < n;i++){
			if(i >= k) a[i%k] += a[i];
		}
		int ans = 0;
		sort(a,a+k,greater<int>());
		for(int i = 0;i < r;i++){
			ans += a[i];
		}
        printf("%d\n",ans);
	} 
}

H - 小w的半阶乘平方

题目描述

小w最近对于阶乘方面比较感兴趣，对于阶乘运算其实有很多的变体运算，比如“双阶乘”。
小w现在也定义了一种叫做“半阶乘”的运算。
假设p为质数，halfact=⌊p/2⌋! mod p
现在请你告诉小w， halfact^2 mod p后的结果。
即求1^2 × 2^2 × 3^2 × 4^2 × … × ⌊p/2⌋^2 mod p

Input

第一行输入一个正整数T(1≤T≤1e5)表示样例的组数。
接下来T行，每行输入一个正质数p。(1≤p≤1e9)

Output

对于每组样例，输出一个非负整数表示答案。

Sample Input

2
5
7

Sample Output

4
1

理解

5/2=2,1×2≡2(mod5),2^2≡4(mod5)
7/2=3,1×2×3≡6(mod7),6^2≡1(mod7)

AC代码

#include
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
typedef long long ll;
typedef pair <int,int> PAIR;
const int maxn = 5e5 + 7;
const double pi = acos(-1);
const ll mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;

int main(){
	int cas;
	scanf("%d",&cas);
	while(cas--){
		ll n;
		scanf("%lld",&n);
		if(n % 4 == 1) printf("%lld\n",n-1);
		else printf("1\n");
	}
	return 0;
}

二、宁波市多校训练（二）

C - 树行棋

题目描述

小w有两个好朋友，分别是doge汪和doge喵，一天，doge汪和doge喵在玩一种名叫树行棋的棋。规则是这样的。
棋盘是一个有根多叉树，多叉树的根节点为0号节点。并且除了根节点以外，其余节点上面有一些棋子。且第i个节点上面棋子的个数为a[i]。
两个人轮流行动，doge汪先手。每次行动的人都可以选中除根节点以外，任何一个有棋子的节点，并且选择将该节点上的一些棋子向父亲节点移动一步，可以将该节点上面的棋子全选，但是至少需要选中1个。如果在某人行动后，所有棋子均位于根节点，则那个人获胜。
doge汪和doge喵都是绝顶聪明的博弈高手，如果doge汪先手，请问谁将获得最终的胜利。

Input

第一行是一个正整数T，表示有T组案例。
对于每组案例，第一行是一个正整数n(1≤n≤106)，表示除根节点（0号节点）以外，树还有几个节点。
接下来两行，第一行共n个整数，表示第i个节点的父亲节点是谁，数据保证fa[i] 第二行共n个整数，表示第i个节点上面一开始有几个棋子，保证0≤a[i]≤106。
保证一开始至少有一个棋子

Output

对于每组案例，输出一行一个字符串。
如果doge汪（先手）最终取得胜利，请输出"dogewang"。
如果doge喵（后手）最终取得胜利，请输出"dogenya"。

Sample Input

4
3
0 0 0
1 2 1
5
0 0 0 1 1
1 2 3 4 4
5
0 0 0 2 2
5 6 1 1 2
6
0 0 1 1 2 2
6 6 1 2 4 7

Sample Output

dogewang
dogenya
dogewang
dogenya

Hint

 nyanya~nya~nyanyanya~nyanya~nyanyanyanya~nya~nyanya.......

AC代码

#include
#define pb push_back
using namespace std;
typedef long long ll;
const int N = 1e6+5;

int fa[N],a[N],dep[N];

int main()
{
	int n,x,T;
	scanf("%d",&T);
	while(T--){
		scanf("%d",&n);
		for(int i = 1;i <= n;++i) scanf("%d",&x),fa[i] = x;
		for(int i = 1;i <= n;++i) scanf("%d",&a[i]);
		
		int ans = 0;
		memset(dep,0,sizeof(dep));
		for(int i = 1;i <= n;++i) dep[i] = dep[fa[i]]^1;
		for(int i = 1;i <= n;++i) if(dep[i]) ans ^= a[i];
		if(ans) printf("dogewang\n");
		else printf("dogenya\n"); 
	}
	return 0;
}

D - LCA！

题目描述

给定一颗有根树，对于树上的任意一点x来说，树上从根节点到x节点所构成简单路径上所有的节点均为x的祖先（包括x节点本身）。那么对于树上任意两点x,y,如果z同时是x和y的祖先，则称z为x和y的公共祖先。
x和y的最近公共祖先指所有x和y的公共祖先中深度最高的点，记为lca(x,y)。
如果树结构确定，并且x和y的值给定，那么lca(x,y)的值将只与根节点有关。
所以就可以定义无根树的lca(root,x,y)表示求以root为根时，x和y的最近公共祖先。
请你编写程序，计算在无根树结构给定情况下的lca(root,x,y)。

Input

测试数据将分为10个不同的文件输入，对于每个输入文件
第一行是一个整数n(2≤n≤100000)，表示树有n个节点。
接下来n-1行每行两个正整数u,v(1≤u,v≤n)表示树上的一条边。
然后是一行一个整数m(1≤m≤100000)，表示有m个查询。
接下来m行，每行三个整数root,x,y(1≤x,y,z≤n)表示询问lca(root,x,y)。

Output

请输出m行，每行一个正整数，表示询问的答案。

Sample Input

11
1 2
2 3
3 4
3 8
1 5
5 9
5 7
5 6
6 11
10 6
12
2 4 1
10 7 6
11 8 7
1 5 2
7 6 11
10 1 9
1 5 7
7 5 1
5 7 1
1 4 11
5 9 10
5 10 11

Sample Output

2
6
5
1
6
5
5
5
5
1
5
6

Hint

树结构如下

lca(2,4,1)=2
lca(10,7,6)=6
lca(11,8,7)=5
lca(1,5,2)=1
lca(7,6,11)=6
lca(10,1,9)=5
lca(1,5,7)=5
lca(7,5,1)=5
lca(5,7,1)=5
lca(1,4,11)=1
lca(5,9,10)=5
lca(2,4,1)=2
lca(5,10,11)=6
对于样例1，n,m<=100，树结构为随机生成。
对于样例2,3，n,m<=1000,树结构为随机生成。
对于样例4,n,m<=100000，树为完全二叉树，1为树根，且保证查询中root恒等于1。
对于样例5, n,m<=100000，树为完全二叉树。
对于样例6,7,n,m<=100000，树完全退化为一条树链。
对于样例8,9，n,m<=100000，树为随机生成。
对于样例10，树的最长链>50000，但不完全退化为一条链。
对于全部的样例，保证查询中x≠y

AC代码

#include
using namespace std;
typedef long long ll;
const int N = 1e5+7;

struct node{
	int to,next;
	node(){}
	node(int to,int nex):to(to),next(nex){}
} e[N << 1];
int head[N],tot; 
int size[N],son[N],dep[N],faz[N];
inline void dfs1(int u,int f,int deep){
	dep[u] = deep;faz[u] = f;size[u] = 1;son[u] = -1;
	
	int maxi = -1;
	for(int i = head[u];~i;i = e[i].next){
		int v = e[i].to;
		if(v == f) continue;
		dfs1(v,u,deep+1);
		size[u] += size[v];
		if(maxi < size[v]) maxi = size[v],son[u] = v;
	}
	return ;
} 
int top[N],dfn[N],id[N],cnt;
inline void dfs2(int u,int rt){
	dfn[u] = ++cnt;id[cnt] = u;top[u] = rt;
	
	if(~son[u]) dfs2(son[u],rt);
	for(int i = head[u];~i;i = e[i].next){
		int v = e[i].to;
		if(v == faz[u] || v == son[u]) continue;
		dfs2(v,v);
	}
	return ;
} 
inline void add(int u,int v){
	e[tot] = node(v,head[u]);head[u] = tot++;
	e[tot] = node(u,head[v]);head[v] = tot++;
} 
inline int lca(int u,int v){
	while(top[u] != top[v]){
		if(dep[top[u]] < dep[top[v]]) swap(u,v);
		u = faz[top[u]];
	}
	if(dep[u] > dep[v]) swap(u,v);
	return u;
}

int main(){
	int n;
	scanf("%d",&n);
	for(int i = 1;i <= n;++i) head[i] = -1;
	tot = cnt = 0;
	
	int u,v;
	for(int i = 1;i < n;++i){
		scanf("%d%d",&u,&v);
		add(u,v);
	} 
	dfs1(1,1,1);
	dfs2(1,1); 
	int q;
	scanf("%d",&q);
	while(q--){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z); 
		int LCA1 = lca(x,y);
		int LCA2 = lca(x,z);
		int LCA3 = lca(y,z); 
		if(LCA1 == LCA2 && LCA2 == LCA3) printf("%d\n",LCA1);
		else if(LCA1 == LCA2) printf("%d\n",LCA3);
		else if(LCA1 == LCA3) printf("%d\n",LCA2);
		else printf("%d\n",LCA1);
	}
	return 0;
}

E - 最大限定倍数(Easy Version)

题目描述

本题有对应的Normal Version，Normal Version和Easy Version的区别仅在数据范围。通过Normal Version可直接AC Easy Version。
小w定义一个数x关于n的MLM(最大限定倍数 maxlimitmultiple)为所有x的正整数倍数中不大于n最大的那个。
例如3关于7的MLM就是6，9关于100的MLM是99。
现在小w想要知道∑ni=1MLM(i)是多少（1…n关于n的MLM之和）。

Input

仅一行，输入一个正整数n(1≤n≤1e5)

Output

仅一个正整数表示问题的答案

Sample Input

Sample Output

Hint

1的倍数中不大于7的是7
2的倍数中不大于7的是6
3的倍数中不大于7的是6
4的倍数中不大于7的是4
5的倍数中不大于7的是5
6的倍数中不大于7的是6
7的倍数中不大于7的是7
7+6+6+4+5+6+7=41

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;

int main(){
	int n;
	scanf("%d",&n);
	ll ans = 0;
	for(int i = 1;i <= n;i++){
		ans += (n/i) * i;
	}
	cout << ans << endl;
	return 0;
}

F - 最大限定倍数(Normal Version)

题目描述

本题有对应的Easy Version，Normal Version和Easy Version的区别仅在数据范围。通过Normal Version可直接AC Easy Version。
小w定义一个数x关于n的MLM(最大限定倍数 maxlimitmultiple)为所有x的正整数倍数中不大于n最大的那个。
例如3关于7的MLM就是6，9关于100的MLM是99。
现在小w想要知道∑ni=1MLM(i)是多少（1…n关于n的MLM之和）。

Input

仅一行，输入一个正整数n(1≤n≤2×1e9)

Output

仅一个正整数表示问题的答案

Sample Input

Sample Output

Hint

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;

int main(){
	ll n;
	scanf("%lld",&n);
	ll ans = 0;
	ll w = n;
	for(ll i = 1;i <= n;i++){
		ll t = n / (i+1) + 1;
		ans = ans + (w + t) * (w - t + 1) / 2 * i;
		w = t - 1;
		if(t == 1) break;
		i = (n / (t-1)) - 1;
	}
	printf("%lld\n",ans);
	return 0;
}

H - 棋盘(Easy Version)

题目描述

本题有对应的Hard Version,Easy Version与Hard Version之间的差异仅在数据范围不同，通过Hard Version的代码可直接AC Easy Version
由于是Easy Version，增加了额外的限制条件，保证输入的n=4
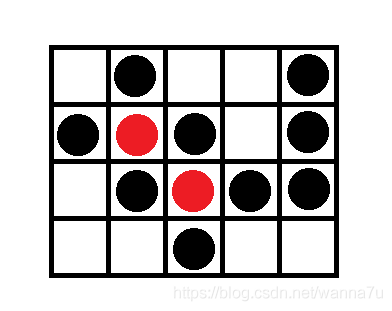
小w有一个4*5（4行5列）的棋盘，棋盘上面已经放了若干个棋子，如图所示。

现在小w想再往棋盘上放置一些棋子，使得所有的棋子连成一片。问小w最少再放多少个棋子。
我们认为一枚的棋子与其上下左右四个方向相邻的棋子是同一片。
同时，如果a棋子与b棋子是同一片，并且b棋子与c棋子是同一片，则a棋子与c棋子也是同一片。

Input

第一行是一个整数n(n=4)
接下来n行，每行一个长度为5的01串。0表示该位置没有棋子。1表示该位置已有棋子。

Output

仅一行一个非负整数，表示还需放置多少个棋子。

Sample Input

4
01001
10101
01011
00100

Sample Output

Hint

放置两个棋子，如图所示

AC代码

#include
using namespace std;
typedef long long ll;
const int N = 10;

int mp[N][N],ne[N][N],n;
bool vis[N][N];
int mvx[] = {1,0,0,-1};
int mvy[] = {0,1,-1,0};

inline bool judge(int x,int y){
	return !(x < 0 || x >= n || y < 0 || y >= 5 || !ne[x][y] || vis[x][y]);
}

inline void dfs(int x,int y){
	vis[x][y] = 1;
	for(int i = 0;i < 4;++i){
		int tx = x+mvx[i];
		int ty = y+mvy[i];
		if(judge(tx,ty))
			dfs(tx,ty);
	}
	return ;
}

inline bool check(){
	for(int i = 0;i < n;++i)
		for(int j = 0;j < 5;++j)
			vis[i][j] = 0;

	int res = 0;
	for(int i = 0;i < n;++i){
		for(int j = 0;j < 5;++j){
			if(ne[i][j]){
				if(vis[i][j]) continue;
				res++;
				if(res > 1) return 0;
				dfs(i,j);
			}
		}
	}
	return res == 1;
}

int main()
{
	int ans = 0;
	scanf("%d",&n);
	for(int i = 0;i < n;++i)
		for(int j = 0;j < 5;++j){
			scanf("%1d",&mp[i][j]);
			if(!mp[i][j]) ans++;
		}
	int p = (n*5);
	
	if(ans == p){
		printf("0\n");
		return 0;
	}
	
	for(int ac = 0;ac < (1 << p);++ac){
		int res = 0;
		for(int i = 0;i < n;++i){
			for(int j = 0;j < 5;++j){
				ne[i][j] = mp[i][j];
				int k = i*5+j;
				
				if(!(ac & (1 << k)) && mp[i][j]) res = 50;
				if((ac & (1 << k)) && !mp[i][j]){
					res++;
					ne[i][j] = 1;
				}
				if(res > ans) break;
			}
			if(res > ans) break;
		}
		if(res > ans) continue;
		if(check()) ans = min(ans,res);
	}
	
	printf("%d\n",ans);
	return 0;
}

三、宁波市多校训练（三）

A - C语言头文件识别器

题目描述

我们在编写C代码的时候首先要声明所使用的头文件。在C语言家族程序中，头文件被大量使用。一般而言，每个C++/C程序通常由头文件和定义文件组成。头文件作为一种包含功能函数、数据接口声明的载体文件，主要用于保存程序的声明，而定义文件用于保存程序的实现。现在给你一个C语言源文件，首先输入一个正整数n,表示文件的行数，接下来输入n行表示该C的源文件，请你告诉我该程序所使用的头文件种类数目。

Input

首先输入一个正整数n(1≤n≤100)表示文件的行数，接下来输入n行表示该C的源文件。

Output

输出一个整数表示该程序所使用的头文件种类数，保证至少使用了一个以上的头文件。

Sample Input

12
#include
#include
#include
#include
#define ll long long
int main()
{
int a,b;
scanf("%d %d",&a,&b);
printf("%d\n",a+b);
return 0;
}

Sample Output

Hint

输入数据保证是可以被执行的C代码，并且头文件一定按照"#include“的形式给出，XXXX为头文件名称，并且保证头文件声明的行中不含有空格，一定顶格给出。
保证所有的头文件声明均写在主函数的上面，符合C语言规范要求。
上述样例中包含了"stdio.h”,“math.h”,“stdlib.h”，三种不同的头文件，注意重复包含不能算重。所以输出3

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
map<string,int> mp;

int main(){
	int n;
	scanf("%d",&n);
	getchar();
	int sum = 0;
	for(int i = 1;i <= n;i++){
		string s;
		getline(cin,s);
		if(s.size() < 8) continue;
		string t = s.substr(0,8);
		if(t == "#include"){
				if(mp[s]) continue;
				else{
					mp[s] = 1;
					sum++;
				}
			}
	}
	cout << sum << endl;
	return 0;	
}

B - 小w和小doge的互质数(Easy Version)

题目描述

本题有对应的Hard Version，Easy Version与Hard Version之间的区别仅在数据范围不同，通过Hard Version的代码可直接AC Easy Version
众所周知，小w和小doge是一对好朋友。
小w有n个正整数ai，小doge有m个正整数bi。
这天他们两个凑到一起互相看到了对方手里的正整数。
他们想要知道，对于自己手中的每个正整数，对方有多少个数字与其互质（即这两个整数的gcd=1）。
请你依次告诉他们每个人，对于他们手里的每个数字，对方有多少个正整数与其互质。
我们认为数字1与所有数都是互质的。

Input

第一行输入两个正整数n,m(1≤n,m≤1e2)表示小w手中有n个正整数，小doge手中有m个正整数。
接下来一行输入n个正整数ai(1≤ai≤1e6)
接下来一行输入m个正整数bi(1≤bi≤1e6)

Output

输出两行
第一行n个正整数表示小w手中的每个数字，小doge手中有多少个整数能与之互质。输出的整数之间用一个空格隔开且行末不允许有多余空格
第二行m个正整数表示小doge手中的每个数字，小w手中有多少个整数能与之互质。输出的整数之间用一个空格隔开且行末不允许有多余空格

Sample Input

5 4
14 6 6 12 42
2 7 6 3

Sample Output

1 1 1 1 0
0 3 0 1

Hint

对于c++，头文件
#include
中内置了求两个整数的最大公约数的函数__gcd()
可以用条件表达式 __gcd(a,b)==1 来判断整数a与b是否互质。

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
map<string,int> mp;
ll a[107],b[107];
inline ll gcd(ll a,ll b){
	return b ?gcd(b,a%b) :a;
}
int main(){
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i <= n;i++){
		scanf("%lld",&a[i]);
	}
	for(int i = 1;i <= m;i++){
		scanf("%lld",&b[i]);
	}
	for(int i = 1;i <= n;i++){
		int sum = 0;
		for(int j = 1;j <= m;j++){
			if(gcd(a[i],b[j]) == 1) sum++;
		}
		printf("%d%c",sum,i == n ?'\n' :' ');
	}
	for(int i = 1;i <= m;++i){
		int sum = 0;
		for(int j = 1;j <= n;++j){
			if(gcd(b[i],a[j]) == 1)
				sum++;
		}
		printf("%d%c",sum,i == m ?'\n' :' ');
	}
	return 0;	
}

D - 礼物分配问题(Easy Version)

题目描述

本题有对应的Hard Version，Easy Version增加了额外的限制条件，通过Hard Version的代码可直接AC Easy Version。
由于是Easy Version增加了限制条件：一个人最多喜欢两件礼物，同时一件礼物也最多同时被两个人喜欢。
小w有n个好朋友，他想给这n个朋友送一些礼物。他现在准备了共m个礼物送给他们。
每个朋友有一个喜好物品的列表，比如1号朋友喜欢1,2,3,4号礼物，2号朋友喜欢2,3号礼物。
如果一个人收到两件及以上他喜好列表中的礼物时，他就会很开心。
现在每个礼物只能送给一个人，每个人可以收到多个礼物。
小w想知道他最多能让多少朋友开心？

Input

第一行是一个正整数T(1≤T≤20)，表示有T组案例
对于每组案例：第一行是两个正整数n,m,(1≤n≤300,1≤m≤600)表示小w的n个朋友和手中的m个礼物
接下来n行每行第一个正整数ki(0≤ki≤2)表示第i个朋友喜好礼物的个数，并且接下来ki个正整数likej，1≤likej≤m表示第i个朋友喜欢的第j个物品的编号
Easy Version限制条件：一个人最多喜欢两件礼物，同时一件礼物也最多同时被两个人喜欢。

Output

对于每组案例，输出仅一个整数，表示最多能让多少个朋友开心。

Sample Input

3
2 3
2 1 2
2 2 3
4 4
2 1 2
2 2 3
2 4 3
2 1 4
3 2
1 1
0
2 1 2

Sample Output

1
2
1

Hint

对于第一组样例：
送给第一个人1号和2号礼物。
有1个人开心。
对于第二组样例：
送给第一个人1号和2号礼物。
送给第三个人3号和4号礼物、
有2个人开心。
对于第三组样例：
因为第一个人只有喜欢一种礼物，第二个人没有喜欢的礼物。所以无论怎样他们都不会开心。
所以送给第三个人1号和2号礼物。
有1个人开心。

AC代码

#include
using namespace std;
typedef long long ll;
const double PI = acos(-1.0);
const double eps = 1e-6;
const int INF = 1000000000;
const int mod = 1e9+7;
const int maxn = 2e5+7;

int ip[1005],ig[1005];
int main() {
	int T;
    scanf("%d",&T);
    while(T--) {
    	vector<int> p[305],g[605];
    	memset(ip,0,sizeof(ip));
    	memset(ig,0,sizeof(ig)); 
		int n,m;
		cin>>n>>m;
		for(int i=1;i<=n;i++){
			int t,x;
			cin>>t;
			if(t==0){
				ip[i] = 1;
				continue;
			}
			if(t==1){
				cin>>x;
				ip[i] = 1;
				continue;
			}
			for(int j=1;j<=t;j++){
				cin>>x;
				p[i].push_back(x);
				g[x].push_back(i);
			} 
		}
		int cnt = 0;
		for(int i=1;i<=m;i++){
			if(g[i].size()==1&&ig[i]==0&&ip[g[i][0]]==0){
				if(ig[p[g[i][0]][0]]==0&&ig[p[g[i][0]][1]]==0){
					ip[i] = 1;
					cnt++;
					ig[p[g[i][0]][0]] = 1;
					ig[p[g[i][0]][1]] = 1;
				}
			}
		}
		for(int i=1;i<=n;i++){
			if(ip[i]==0&&p[i].size()>1&&ig[p[i][0]]==0&&ig[p[i][1]]==0){
				cnt++;
				ig[p[i][0]] = 1;
				ig[p[i][1]] = 1;
				ip[i] = 1;
			}
		}
		cout<<cnt<<endl;
    }
    return 0;
}

C -

题目描述

Input

Output

Sample Input

Sample Output

Hint

理解

这是一个线段树辅助二分查找这么个套路的题。 
用线段树保存 区间最大剩余体积的篮子 然后很显然， 
如果这段区间内最大体积的篮子 可以放得下这些鸡蛋， 
就说明区间内至少有一个篮子放得下（比如最大的）。 
然后使用线段树辅助进行二分查找， 
也就是说一开始在根节点的时候，左子树的节点 表示1~n/2的区间，右子树表示 n/2+1~n的区间， 
然后你不是知道区间最大篮子的剩 余体积嘛，用左子树的剩余最大体积去比， 
如果左边放不下，就往右子树递归二分， 反之就往左子树递归二分。  
最终到达叶子节点的时候就是我们要放的篮子。

AC代码

#include 
#define ALL 1,1,n
#define ls rt << 1
#define rs rt << 1|1
#define lson ls,l,m
#define rson rs,m+1,r
using namespace std;
const int N = 3e5+5;

struct node{
	int cnt,size;
} t[N << 2];
int n,m,k;
void pushup(int rt){
	t[rt].size = max(t[ls].size,t[rs].size);
}
void build(int rt,int l,int r){
	if(l == r){
		t[rt].cnt = k;
		t[rt].size = m;
		return ;
	}
	int m = (l+r) >> 1;
	build(lson);build(rson);
	pushup(rt);
}
int cal(int rt,int l,int r,int x){
	if(l == r){
		t[rt].cnt--;
		if(t[rt].cnt == 0) t[rt].size = 0;
		else t[rt].size -= x;
		return l;
	}
	int m = (l+r) >> 1,res;
	if(t[ls].size >= x) res = cal(lson,x);
	else res = cal(rson,x);
	pushup(rt);
	return res;
}

int main()
{
	int x,T;
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d",&n,&m,&k);
		build(ALL);
		for(int i = 1;i <= n;++i){
			scanf("%d",&x);
			if(t[1].size < x) printf("-1\n");
			else printf("%d\n",cal(ALL,x));
		}
	}
	return 0;
}

四、宁波市多校训练（四）

A - 炉石传说——按费拍怪是王道

题目描述

哈总最近迷上了《炉石传说》这个游戏，这是一个回合制的卡牌游戏，每个回合每个玩家会有一定数量的法力水晶，你可以花费水晶来使用卡牌，具体的水晶数量是：第一回合有且只有一个法力水晶，第二回合有且只有两个法力水晶，以此类推……此外，到了第十回合以后就保持每回合十个法力水晶，直到游戏结束。假如你现在手里有n张卡牌，使用一张牌需要花费个法力水晶。只要法力水晶足够，每回合可以使用的卡牌数量不限，问至少多少回合能将手里的卡牌全部用完(不考虑抽牌)？如果到了第15回合结束后还有剩余的卡牌，则视为无法使用完毕。

Input

输入共两行，
第一行为一个整数n(1≤n≤10)表示手中卡牌数量。
第二行有n个整数a1…an,其中 ai(0≤ai≤10)表示使用第i张卡牌时花费的法力水晶数量。

Output

输出一个数字，表示打完全部手牌所需的最少回合数，若15回合无法使用完毕则输出“-1”。

Sample Input

样例输入1
4
1 2 1 2

样例输入2
9
2 2 2 2 3 3 4 4 5

Sample Output

样例输出1
3
样例输出2
7

Hint

对于样例1，第一回合花费1个法力水晶使用第一张卡，第一回合花费2个法力水晶使用第二张卡，第三回合花费3个法力水晶使用第三第四共两张卡。
对于样例2，第二回合花费2个法力水晶使用第一张卡，第三回合花费3个法力水晶使用第五张卡，第四回合花费4个法力水晶使用第七张卡，第五回合花费5个法力水晶使用第九张卡，第六回合花费6个法力水晶使用第二、三、四共三张卡，第七回合花费7个法力水晶使用第六第八两张卡，

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
const double esp = 1e-6;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
int a[17],l[27],nw[27];

int main()
{
	for(int i = 1;i <= 10;++i) l[i] = i;
	for(int i = 11;i < 21;++i) l[i] = 10;
	
	int n;
	scanf("%d",&n);
	for(int i = 1;i <= n;++i) scanf("%d",&a[i]);
	sort(a+1,a+n+1);
	
	int pos,ans = 100;
	do{
		pos = 1;
		for(int i = 1;i < 21;++i) nw[i] = 0;
		for(int i = 1;i <= n;++i){
			while(a[i]+nw[pos] > l[pos] && pos < 21) pos++;
			if(a[i]+nw[pos] <= l[pos]) nw[pos] += a[i];
		}
		
		if(!nw[pos]) pos--;
		ans = min(ans,pos);
	}while(next_permutation(a+1,a+n+1));
	
	printf("%d\n",ans > 15 ?-1 :ans);
	return 0;
}

C - 石头划分

题目描述

小明和小蔡在玩一个游戏，需要将n个固定好的石头划分成k组，他们在想如何使得最近的两组石头的组间距离最远（组间距离定义为两组间距离最近的两个石头之间的距离），你可以编程帮帮他们吗？

Input

输入文件第一行包含两个整数 n和k(1≤n,k≤103)，分别代表了石头的数量和分组的数量。
接下来 n 行，每行包含两个整数 x，y(0≤x,y≤104)，描述了一个石头的坐标。

Output

输出一行一个实数，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

Sample Input

9 3
2 2
2 3
3 2
3 3
3 5
3 6
4 6
6 2
6 3

Sample Output

2.00

Hint

因为数据有锅多组读入会wa

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 1010;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7; 
int fa[maxn],n,m,cnt=0; 
struct ss{
     int x;
     int y;
   }e[maxn];

struct node{
     int u;
     int v;
     int w;
   }s[maxn*maxn];

int find(int x){
     if (fa[x]==x) return x;
     fa[x]=find(fa[x]);
     return fa[x];
   }

bool cmp(node a,node b){
     return a.w<b.w;
   }

int main() {
     scanf("%d %d",&n,&m);
     for (int i=1;i<=n;i++)
        scanf("%d %d",&e[i].x,&e[i].y);
     for (int i=1;i<=n;i++)
         for (int j=i+1;j<=n;j++)
            {
                cnt=cnt+1;
                s[cnt].u=i;
                s[cnt].v=j;
                s[cnt].w=(e[j].x-e[i].x)*(e[j].x-e[i].x)+(e[j].y-e[i].y)*(e[j].y-e[i].y);
            }
    sort(s+1,s+cnt+1,cmp);
    int k=n;
    for (int i=1;i<=n;i++) fa[i]=i;
    for (int i=1;i<=cnt;i++)
       {
         int fa1=find(s[i].u),fa2=find(s[i].v);
         if (fa1!=fa2) k--;
            fa[fa1]=fa2;
            if (k<m) {printf("%0.2lf\n",sqrt(s[i].w));return 0;}
        }
   }

D - 树上的点到链

题目描述

有一棵n个节点的树，和m次询问，每次询问给出三个点的序号a,b,s，对于两个确定的节点a和b，树中有且仅有一条路连接这两个点，请在这条路上（包括端点）选择一个点d，使得点s到点d的距离最短，并且输出这个最短距离。

Input

第一行输入两个整数n,m，(3≤n≤100000,1≤m≤10000)，接下来的n−1行给出两个整数表示树上每一条边的两端节点1～n，接下来的m行给出三个整数a,b,s,1≤a,b,s≤100000,a≠b。

Output

对于每一个询问给出一个最短距离的结果。

Sample Input

11 3
1 2
1 3
2 4
2 5
2 6
3 7
3 8
4 9
4 10
6 11
4 8 11
9 10 8
4 6 2

Sample Output

2
4
0

AC代码

#include
#include
using namespace std;

const int maxn=1e5+10;
int n,q,cnt;
bool vis[maxn];
int head[maxn],deep[maxn],dis[maxn],fa[maxn][11] ;    
struct data{int to,next;}e[2*maxn];
void ins(int u,int v)        
{
    e[++cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt;
}
void insert(int u,int v)
{
    ins(u,v);
    ins(v,u);
}
void dfs(int x)   
{
    vis[x]=1;
    for(int i=1;i<=9;i++)
    {
        if(deep[x]<(1<<i)) break;
        fa[x][i]=fa[fa[x][i-1]][i-1];
    }
    for(int i=head[x];i;i=e[i].next)
    {
        if(vis[e[i].to]) continue;
        deep[e[i].to]=deep[x]+1;
        fa[e[i].to][0]=x;
        dfs(e[i].to);
    }
}
int lca(int x,int y)  
{
    if(deep[x]<deep[y]) swap(x,y);
    int d=deep[x]-deep[y];
    for(int i=0;i<=9;i++)
        if((1<<i)&d) x=fa[x][i]; 
    for(int i=9;i>=0;i--)    
        if(fa[x][i]!=fa[y][i])
            {x=fa[x][i];y=fa[y][i];}
    if(x==y) return x;
    else return fa[x][0];  
}

int main(){
    scanf("%d%d",&n,&q);
    for(int i=1;i<n;i++){
        int u, v;
        scanf("%d%d",&u,&v);
        insert(u,v);
    }
    dfs(1);
    for(int i=1;i<=q;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        int a = lca(x,y);
        int b = lca(y,z);
        int c = lca(x,z);
        if (a==b){
            int t = lca(c,z);
            printf("%d\n", deep[c]-deep[t]+deep[z]-deep[t]);
        }else if (a==c){
            int t = lca(b,z);
            printf("%d\n", deep[b]-deep[t]+deep[z]-deep[t]);
        }else{
            int t = lca(a,z);
            printf("%d\n", deep[a]-deep[t]+deep[z]-deep[t]);
        }
    }
    return 0;
}

E - 相同的地板

题目描述

一天，装修商人拉来了一批地板，并号称没有相同花纹的两块地板，小王不相信，请你帮忙检验一下，这里面是否有相同的两块地板。
地板的大小为3×3，有三种花纹分别为#，O，X，印在地板的每个格子上，判断是否有相同的两块地板是一样的。注意：两块地板上的每个格子的花纹都相同，才算一样，因为地板都是方的，旋转90,180,270度和另一块地板一样，也算一样。

Input

第一行是一个正整数n(1≤n≤4000)，表示有n块地板。
接下来3×n行，每3行表示一块地板。

Output

如果有相同花色的两块地板，输出“YES”；
否则输出“NO”。

Sample Input

2
#X#
OOO
#X#
#O#
XOX
#O#

Sample Output

YES

Hint

每块地板只有9个格子大小，只要用map记录下每块地板包括旋转后的状态，遇到相同的状态说明有重复的地板。

AC代码

#include
using namespace std;
typedef long long ll;
const int N = 5e4+5;

string mp[N][5];

inline bool check(int x,int y){
	int cnt = 0;
	for(int i = 1;i <= 3;++i)
		for(int j = 1;j <= 3;++j)
			if(mp[x][i][j-1] == mp[y][i][j-1])
				cnt++;
	if(cnt == 9) return 1;
	
	cnt = 0;
	for(int i = 1;i <= 3;++i)
		for(int j = 1;j <= 3;++j)
			if(mp[x][i][j-1] == mp[y][4-j][i-1])
				cnt++;
	if(cnt == 9) return 1;
	
	cnt = 0;
	for(int i = 1;i <= 3;++i)
		for(int j = 1;j <= 3;++j)
			if(mp[x][i][j-1] == mp[y][4-i][4-j-1])
				cnt++;
	if(cnt == 9) return 1;
	
	cnt = 0;
	for(int i = 1;i <= 3;++i)
		for(int j = 1;j <= 3;++j)
			if(mp[x][i][j-1] == mp[y][j][4-i-1])
				cnt++;
	if(cnt == 9) return 1;
	
	return 0;
}

int main()
{
	int n;
	scanf("%d",&n);
	for(int i = 1;i <= n;++i)
		for(int j = 1;j <= 3;++j)
			cin >> mp[i][j];
		
	for(int i = 1;i <= n;++i)
		for(int j = i+1;j <= n;++j)
			if(check(i,j)){
				printf("YES\n");
				return 0;
			}
	printf("NO\n");
	return 0;
}

G - 隐秘的峡谷

题目描述

张东升喊你去爬山，但这次他不小心进入了一个充满机关的峡谷。这个峡谷是2×n的网格，张东升在（1，1），他需要到达（2，n）才能离开这里。张东升只能移动到相邻的格子，不能斜向移动。
但是在某些时刻，某些位置的状态会发生变化：原本是地面则变成陷阱，无法通过；或者原本是陷阱则变成地面，可以通过。最初，所有的单元格都是可通过的地面。
张东升发现，总共有q个时刻：第i个时刻就会改变单元格（ri，ci）的状态。
张东升想知道q个时刻过后，能否安全地到达出口，他虽然是个数学老师，但还是需要你地帮助

Input

第一行包含整数n，q(2≤n≤105,1≤q≤105)
之后q行每行包含2个整数ri,ci，（1≤ri≤2,1≤ci≤n），表示在第i时刻当前坐标发生变化
确保单元格（1,1）和（2，n）永远不会变化。

Output

对于每次变化，如果可以从单元格（1,1）到单元格（2，n），则输出“Yes”，否则输出“No”。

Sample Input

5 5
2 3
1 4
2 4
2 3
1 4

Sample Output

Yes
No
No
No
Yes

AC代码

#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 1e5+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;

int vis[3][maxn];
int a[3][maxn];
map<int,int> mp;

int main(){
	int n,q;
	scanf("%d %d",&n,&q);
	int f = 0;	
	while(q--){
		int x,y;
		scanf("%d %d",&x,&y);
		if(a[x][y]==0){
			a[x][y]=1;
			if(x==1){
				vis[2][y-1]++;
				vis[2][y]++;
				vis[2][y+1]++;
			}
			else{
				vis[1][y-1]++;
				vis[1][y]++;
				vis[1][y+1]++;
			}
			if(vis[x][y]!=0){
				f++;
			}
		}
		else{
			a[x][y]=0;
			if(vis[x][y]!=0){
				f--;
			}
			if(x==1){
				vis[2][y-1]--;
				vis[2][y]--;
				vis[2][y+1]--;
			}
			else{
				vis[1][y-1]--;
				vis[1][y]--;
				vis[1][y+1]--;
			}
		}
		if(!f) cout << "Yes" << endl;
		else cout << "No" << endl;
	}
	return 0;	
}

五、宁波市多校训练（五）

A - 龙珠

题目描述

鸟山明的《龙珠》作为经典相信大家都看过，现在悟空又要去找新一轮的龙珠了，但由于环境变化原因，地球上的龙珠数量增加了许多，要找大家帮帮忙。假设地球上有N个城市，对于第i个龙珠，会被放在第i个城市（编号从1开始）。现在有两种操作，通过操作T A B，悟空可以用筋斗云把在A龙珠所在城市的龙珠全部搬运到B龙珠所在的城市，通过操作Q A，你需要告诉悟空A龙珠目前所在城市的编号，以及A龙珠目前所在城市的总龙珠数目，以及A龙珠目前的搬运次数。去收集龙珠吧！GO！GO！GO！

Input

输入的第一行是单个正整数T（0 对于每种情况，第一行包含两个整数：N和Q（2 N代表N个城市。
以下Q行每行表示一个操作Q或者T。
T A B：A，B为龙珠编号，与A龙珠处于同一城市的所有龙珠都已搬运到B龙珠所在的城市。您可以假定两个城市是不同的。
Q A：A为龙珠编号，悟空想知道X（A龙珠所在城市的编号），Y（A龙珠所在城市目前的龙珠数目）和Z（A龙珠的搬运次数）。（1≤AB≤N）

Output

对于每个测试用例，输出格式化为样本输出的测试用例编号。
然后，对于每个Q A，输出一行X Y Z，其中三个Y X Z由空格分隔。

Sample Input

2
3 3
T 1 2
T 3 2
Q 2
3 4
T 1 2
Q 1
T 1 3
Q 1

Sample Output

Case 1:
2 3 0
Case 2:
2 2 1
3 3 2

AC代码

#include
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 1e4+7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 998244353;
int f[maxn];
int sum[maxn];
int find(int k){
    if(k!=f[k]) f[k]=find(f[k]);
    return f[k];
}
int main(){
	int cas;
	scanf("%d",&cas);
	for(int e = 1;e <= cas;e++){
		int n,q;
		scanf("%d %d",&n,&q);
		printf("Case %d:\n",e);
		for(int i = 1;i <= n;i++){
			f[i] = i;
			sum[i] = 0;
		}
		while(q--){
			char c;
			cin >> c;
			if(c == 'T'){
				int a,b;
				scanf("%d %d",&a,&b);
				int u = find(a); //当前所在 
				int v = find(b); //即将进入 
				if(u != v){
					for(int i = 1;i <= n;i++){
						if(f[i] == f[u] && i != b){
							sum[i]++;
							f[i] = v;
						}
					}
				}				
			}else{
				int a;
				scanf("%d",&a);
				int ans = 0;
				for(int i = 1;i <= n;i++){
					if(f[a] == f[i]) ans++;
				}
				printf("%d %d %d\n",f[a],ans,sum[a]);
			}
		}
	} 
    return 0;
}

B - 少抢了多少红包

题目描述

大家都喜欢在微信群中抢红包，但是有时候同一个时刻发出的红包太多，同时抢红包的人数也太多，从而不得不错失一些红包。
小明也喜欢抢红包，但他同时也喜欢想东想西。有天他在一段时间内抢到了不少的红包，不过他觉得他本应该可以抢到更多的红包数量，只不过是方案不对，现他决定求助你，请你编程计算出他究竟少抢了多少个红包。
小明将会提供给你一段时间内出现的红包总数和每个红包出现的时刻与所在的群聊（所在群聊被标记为1-10共10个不同的编号）及小明抢的红包总数。
这10个群里已经稳定排列在小明的聊天列表中，其中标号1的群里在最顶端，标号2，3，4···10依次向下排列，保证群聊的次序不会因新消息的出现打乱。
开始时刻（即0时刻）小明处于紧盯5号群聊的状态（即他在此时可以选择抢并且会成功抢到4，5，6号群聊其中之一在0时刻发出的所有红包，并随后可以将紧盯的群聊变换成4或6号群聊------目光上移一格或者下移一格，当然也可以继续紧盯5号，随即会到达1时刻。）注：1.必须先抢红包再目光移动，如果此时刻没有可抢红包则下一时刻到来前不再抢红包直接目光移动。2.同一个时刻同一个群聊可能会发出多个红包，所有红包在发出时刻的下一时刻到来前如果不被小明抢走将全部会被它人抢走。

Input

多组输入，每组测试数据第一行输入两个整数n,m(0≤m≤n≤100000)分别代表一段时间内出现的红包总数和小明在该段时间内抢到的红包总数。接下来n行每行两个整数a,b,(1≤a≤10,b≤100000)其中a为群聊序号，b为时刻。当输入m=0并且n=0时结束输入。保证小明抢到的红包总数小于等于这段时间内在最优策略下抢到的红包总数。

Output

每组测试样例输出一行，包含一个整数为小明相较于最优策略小明少抢的红包数。

Sample Input

6 3
5 1
4 1
6 1
7 2
7 2
8 3
0 0

Sample Output

AC代码

#include
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 7;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
int dp[maxn][17];
int tp[17];

int main(){
	int n,m;
	while(~scanf("%d %d",&n,&m)){
		if(n == 0 && m == 0) break;
		memset(dp,0,sizeof(dp));
		memset(tp,0,sizeof(tp));
		int mx = 0;
		for(int i = 1;i <= n;i++){
			int u,v;
			scanf("%d %d",&u,&v);
			dp[v][u]++;
			mx = max(mx,v);
		}
		for(int i = mx;i >= 0;i--){
			for(int j = 1;j <= 10;j++){
				tp[j] = dp[i][j]; 
			}
			for(int j = 1;j <= 10;j++){
				dp[i][j] = max(tp[j],max(tp[j-1],tp[j+1])) + max(dp[i+1][j+1],max(dp[i+1][j],dp[i+1][j-1]));
				
			}
		}
		printf("%d\n",dp[0][5] - m);
	}
	return 0;
}

D - 小伙子找姑娘

题目描述

一个岛上有n个小伙子和n个姑娘，如果每个小伙子都爱慕k个姑娘并且每个姑娘都爱慕k个小伙子，那么每个人都能和自己爱慕的人结婚。不过现在的情况是，每个小伙子只喜欢一位姑娘，这位姑娘也只喜欢这一位小伙子，并且每个小伙子都有喜欢的姑娘，每位姑娘都有喜欢的小伙子。可惜，最后只有m位小伙子找到了喜欢的姑娘，其他小伙子只能和不喜欢的姑娘在一起。你要求这样的配对方式有多少种。

Input

第一行一个整数T(T≤20)，代表测试组数。
接下来T行，每行包含两个非负整数n，m（m≤n≤500000）

Output

每组输出一行一个整数，代表配对方式的总数，最后的结果可能非常大，你需要将结果对956452433取模。

Sample Input

3
3 2
1 1
6 3

Sample Output

0
1
40

Hint

样例解释6 3。
假设有6为小伙子，6位姑娘，并且下标相同的互相喜欢，题目要求的是——3对成功匹配，3对错误匹配的情况总数。下面是2种可能的情况：

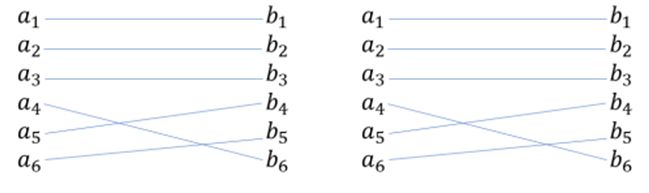
AC代码

#include
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int maxn = 5e5;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
const ll mod = 956452433;
ll a[maxn+7];
ll jc[maxn+7],inv[maxn+7];
bool ispri[maxn+7];
int prime[maxn+7];
int priCnt;
ll qpow(ll a, ll n){
    ll ans = 1;
    while(n){
        if(n&1)        //如果n的当前末位为1
            ans *= a;  //ans乘上当前的a
        a *= a;        //a自乘
        n >>= 1;       //n往右移一位
    }
    return ans;
}
void CalPrime(){
    priCnt = 0;
    memset(ispri,0,sizeof(ispri));
    for(int i = 2;i <= maxn; ++i){
        if(ispri[i] == 0){
            prime[priCnt++] = i;
            for(int j = i+i;j <= maxn; j += i)
                ispri[j] = 1;
        }
    }
} 
ll DivideByPrime(ll N,ll P){
    ll ans = 0;
    while(N) ans += N/P,N /= P;
    return ans;
}
ll CalCnmModP(ll N,ll M,ll P){
    ll ans = 1;
    for(int i = 0 ;i < priCnt && prime[i] <= N; ++i){
        ll x = DivideByPrime(N,prime[i]);
        ll y = DivideByPrime(N-M,prime[i]);
        ll z = DivideByPrime(M,prime[i]);
 
        x -= (y+z);
 
        ans *= qpow(prime[i],x);
        ans %= P;
    }
    return ans;
}
int main(){
	a[0] = 0; a[1] = 0; a[2] = 1; a[3] = 2;
	for(int i = 4;i <= maxn;i++){
		a[i] = (i-1)*(a[i-1]+a[i-2]) % mod;
	}
	CalPrime();
	int cas;
	scanf("%d",&cas);
	while(cas--){
		int n,m;
		scanf("%d %d",&n,&m);
		if(n == m) printf("1\n");
		else if(n == m + 1) printf("0\n");
		else{
			ll sum = CalCnmModP(n,m,mod);
			printf("%d\n",(a[n-m]*sum)%mod);
		}	
	}
    return 0;
}

六、宁波市多校训练（六）

C - 分享蛋糕（Easy）

题目描述

今天是小Z生日，他买了一个蛋糕，要分享给室友尝尝。因为有n个人，现在他把蛋糕均匀地分成n份，分给每一个人。
但是，别人手里的蛋糕总是更好吃的！所以他提出一个玩法，每个人都可以和别人交换最多一次蛋糕，这个玩法有很多种可能的方案，你能计算出可能的方案数吗？

Input

第一行输入一个数n(n≤106)，表示有n个人。

Output

输出一个数表示所有可能的方案总数。（由于这个数可能会很大，所以要mod 109+7后输出）

Sample Input

Sample Output

Hint

假设有n=2，第一个人手里的蛋糕编号为1，第二个人手里的蛋糕编号为2，他们可以选择交换或者不交换，那么最终蛋糕有两种排序方式，分别为1 2和2 1，所以方案数为2。

AC代码

#include
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
typedef long long ll;
typedef pair <int,int> PAIR;
const int maxn = 1e6 + 7;
const double pi = acos(-1);
const ll mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
ll f[maxn];

int main(){
	int n;
	scanf("%d",&n);
	ll sum = 0;
	f[1] = 1ll; f[2] = 2ll;
	for(int i = 3;i < maxn;i++){
		f[i] = (f[i-1] + f[i-2]*(i-1)%mod) % mod;
	}
	cout << f[n] << endl;
	return 0;
}

F - 天天天天想女装

题目描述

天天是宁波大学大二的学生，他有一个特殊的癖好——没错，就是喜欢穿女装！！！但是他又苦于没钱不能经常穿。天天无时无刻都想要买女装！但他又因为不想让别人知道这个特殊癖好，所以请聪明的你想想办法。女装分为上衣和裙子两种，因为天天每一天都想有女装穿，所以他最少需要买两套女装（两件上衣和两件裙子），每件衣服和裙子都有自己对应的开心值，我们需要做的就是帮助天天，让他最开心。购买衣服的数量没有限制，但一件衣服只能买一次，请保证天天最低需求的情况下不要超出天天的预算。

Input

第一行：输入天天的预算金额K，上衣的数量N，裙子的数量M (k,n,m<=50)
第二行：输入N个数，第i个数表示第i件上衣的价格
第三行：输入N个数，第i个数表示第i件上衣的开心值
第四行：输入M个数，第i个数表示第i件裙子的价格
第五行：输入M个数，第i个数表示第i件裙子的开心值

Output

如果能满足天天的最低需求：
第一行输出：YES
第二行输出最大的开心值
如果不能输出NO

Sample Input

10 3 3
1 2 3
4 5 6
1 2 3
9 8 7

Sample Output

YES
34

AC代码

#include
using namespace std;
typedef long long ll;
const int N = 55;
const int INF = 0x3f3f3f3f;

int dp1[N][N],dp2[N][N];
struct node{
	int p,v;
} s[N],x[N];

inline void DP(int n,int k,int dp[][N],node *o){
	for(int i = 1;i <= n;++i)
		for(int s1 = n;s1;--s1)
			for(int mn = k;mn >= o[i].p;--mn)
				if(s1 == 1 || dp[s1-1][mn-o[i].p])
					dp[s1][mn] = max(dp[s1][mn],dp[s1-1][mn-o[i].p]+o[i].v);
	return ;
}

int main()
{
	int k,n,m;
	scanf("%d%d%d",&k,&n,&m);
	for(int i = 1;i <= n;++i) scanf("%d",&s[i].p);
	for(int i = 1;i <= n;++i) scanf("%d",&s[i].v);
	for(int i = 1;i <= m;++i) scanf("%d",&x[i].p);
	for(int i = 1;i <= m;++i) scanf("%d",&x[i].v);
	memset(dp1,0,sizeof(dp1));
	memset(dp2,0,sizeof(dp2));
	
	DP(n,k,dp1,s);
	DP(m,k,dp2,x);
	
	int ans = 0;
	for(int i = 2;i <= n;++i)
		for(int j = 2;j <= m;++j)
			for(int s1 = 0;s1 <= k;++s1)
				for(int s2 = 0;s2 <= k;++s2)
					if(dp1[i][s1] && dp2[j][s2] && s1+s2 <= k)
						ans = max(ans,dp1[i][s1]+dp2[j][s2]);
	
	if(ans) printf("YES\n%d\n",ans);
	else printf("NO\n");
	return 0;
}

G - 猩球崛起

题目描述

吉吉国王在经历在汉诺塔训练之后，感觉到智商明显上升，可以挑战新的难度，为了给吉吉国王新的训练，
现给予他n个{a,b,c…p}不同字符组成的字符串，（n=4则，只能由a,b,c,d四个字符组成）让他进行字符串按字典序升序排列。
询问吉吉国王q次，现有两种询问方式：
第一种，输入目标字符串，问升序过程至目标需要多少步，如(abc到acb)仅需一步，
第二种，询问对原字符串经过k步后的串，如（abc两步后为bac）。
由于忙着去猩球崛起，聪明的你来帮他解决一下吧。

Input

第一行输入n,q，表示有n个不同字符，查询q次；
第二行输入初始字符串，
接下来q行输入操作类型以及询问
3≤n≤16;
1≤q≤10;

Output

对于每个询问输出一行：
对于第一种询问输出升序过程至目标需要多少步。
对于第二种询问输出原字符串经过k步后的串。

Sample Input

3 3
abc
1 bac
2 1
2 1

Sample Output

2
acb
bac

Hint

字典序：（abc→acb→bac→bca→cab→cba）

AC代码

#include
using namespace std;
typedef long long ll;
const int N = 55;
const int INF = 0x3f3f3f3f;

ll kt[] = {1ll,1ll,2ll,6ll,24ll,120ll,720ll,5040ll,40320ll,362880ll,3628800ll,39916800ll,479001600ll,6227020800ll,87178291200ll,1307674368000ll,20922789888000ll};
char s[N];

inline ll get_hash(int n){
	ll hash = 0ll;
	for(int i = 0;i < n;++i){
		ll res = 0;
		for(int j = i+1;j < n;++j){
			if(s[i] > s[j]) res++;
		}
		hash += res*kt[n-i-1];
	}
	return hash;
}

inline void print(ll now,int n){
	vector <int> v;
	vector <int> a;
	for(int i = 0;i < n;++i) v.push_back(i);
	for(int i = n;i;--i){
		ll r = now % kt[i-1];
		ll t = now / kt[i-1];
		now = r;
		sort(v.begin(),v.end());
		a.push_back(v[t]);
		v.erase(v.begin()+t);
	}
	for(int i = 0;i < n;++i) printf("%c",a[i]+'a');
	printf("\n");
}

int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	scanf("%s",s);
	
	ll x,now = get_hash(n);
	int op;
	while(m--){
		scanf("%d",&op);
		if(op == 1){
			scanf("%s",s);
			ll temp = get_hash(n);
			if(temp >= now) printf("%lld\n",temp-now);
			else printf("%lld\n",temp+kt[n]-now);
		}
		else{
			scanf("%lld",&x);
			now += x;
			now %= kt[n];
			print(now,n);
		}
	}
	return 0;
}