先验后验与贝叶斯定理

1.1 条件概率

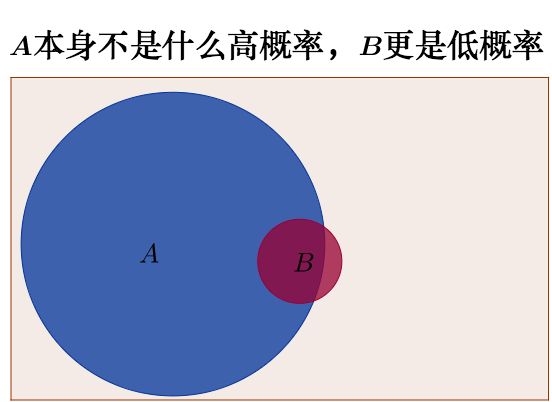
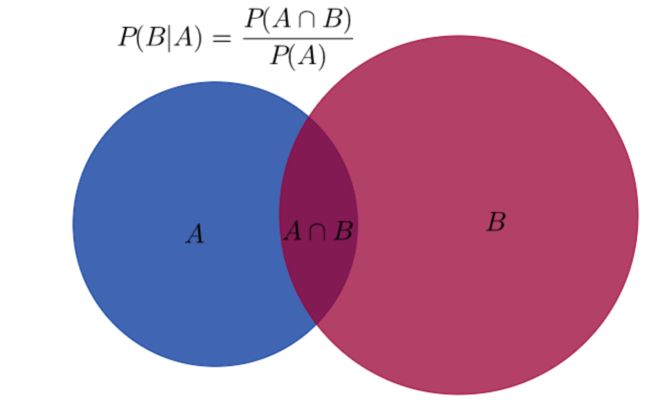
条件概率指在A事件发生的情况下，B事件发生的概率。“A事件发生的情况下”，代表A为样本空间，“B事件发生的概率”，代表$A\cap B$为事件。

因此$P(B|A)=\frac{P(A\cap B)}{P(A)}$

做一下公式变形 $P(A\cap B)=P(B|A)P(A)$

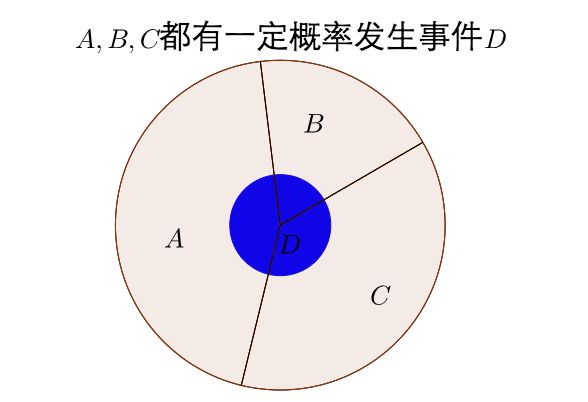
1.2 全概率

可见$P(D)=P(D\cap A)+P(D\cap B)+P(D\cap C)$
由条件概率的公式也可以写成：
$P(D)=P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(AC)$
P(D)就是事件D在全部样本空间S（由A,B,C构成）下发生的概率，称为全概率。
这个式子就是全概率公式。

1.3 贝叶斯定理

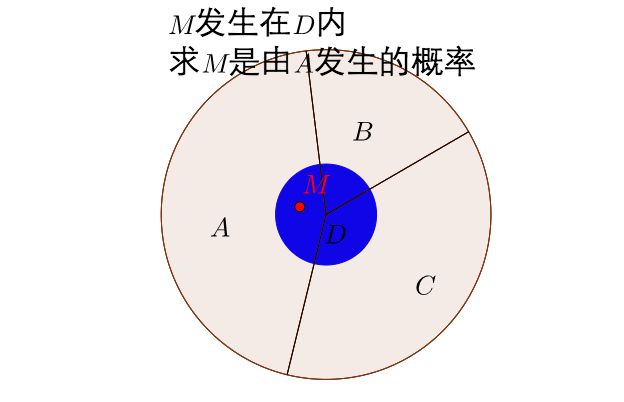
先发生A再发生D的事件：

计算事件在样本空间下的概率P(D|A)

那么，已知M发生在D中，则M发生在A中的概率为：

$P(A|D)=\frac{P(A\cap D)}{P(D)}=\frac{P(A)P(D|A)}{P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(AC)}$

这就是贝叶斯公式

1.3 贝叶斯公式的理解

把上面式子等号右侧拆成两部分来看，则贝叶斯公式的形式为：

$P(A|D)$ = $P(A)$ * $\frac{P(D|A)}{P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(AC)}$

贝叶斯公式实际上阐述了这么一个事情：

后验概率（新信息出现后的A的概率） = 先验概率（A的概率） x 可能性函数（新信息带来的调整）

新信息带来的调整，可以直观的由韦恩图来解释：

1.4 案例：贝叶斯定理的应用

典型应用例如，垃圾邮件过滤，疾病检查，中文分词。

已知某种疾病的发病率是0.001，即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

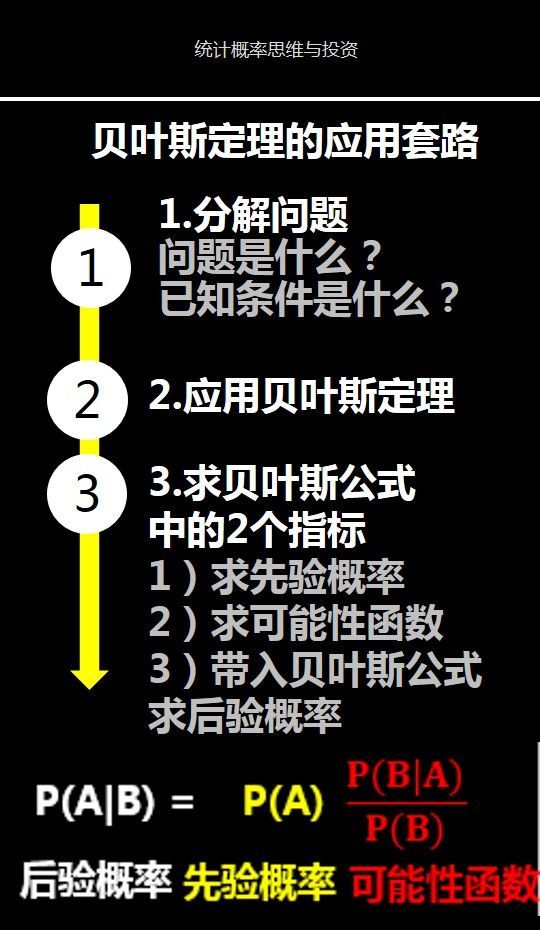
第一步，分解问题
（1）问题是什么：病人的检测结果为阳性，他确实得病的概率有多大？
假定A事件表示得病，B事件表示阳性，那么求解的就是P(A|B）

（2）已知信息
1.疾病发病率为0.001，即P(A)为0.001，
这就是"先验概率"，即没有做试验之前，我们预计的发病率。
2.试剂检测患者是否得病，准确率是0.99，即，患者确实得病的情况下（A），有99%的可能性被检测为阳性（B），也就是P(B|A)=0.99
3.试剂的误报率是5%，即患者没有得病的情况下（事件A的反面，记为A’），有5%的可能呈阳性，也就是P(B|A’)=0.05

综上，已知P(A), P(B|A), P(B|A’)，求P(A|B)，也就是"后验概率"，即做了试验以后，对发病率的估计。

第二步，应用贝叶斯定理
（1）求先验概率
P(A)=0.001
（2）求可能性函数
P(B|A) / P(B)
P(B|A) 表示患者确实得病的情况下试剂呈阳性的概率，也就是0.99
P(B)可以由全概率公式求得，P(B)=P(B|A)P(A)+P(B|A’)P(A’)=0.99 * 0.001 + 0.05 * 0.999 ≈ 0.05
所以可能性函数 P(B|A) / P(B) = 0.99/0.05 = 19.8
（3）带入贝叶斯公式求后验概率
我们得到了一个惊人的结果，P(A|B)约等于0.019。也就是说，即使检验呈现阳性，病人得病的概率，也只是从0.1%增加到了2%左右。这就是所谓的"假阳性"，即阳性结果完全不足以说明病人得病。

为什么这种检验的准确率高达99%，但是可信度却不到2%？答案是与它的误报率太高有关。我们无差别的给一大群人做筛查，而正常人的数目远大于实际患者，所以误差造成的干扰就非常大了。

解决办法是可以先锁定可疑样本，比如10000个人里检查出问题的那10个人，再独立的重复检测一次，而正常人连续两次都出现误差的概率极低，这时筛选出真正患者的准确率就很高了，这也是很多疾病要送交独立机构多次检查的原因。也就是，提高了先验概率，也就有效提高了后验概率。

参考

1.如何理解贝叶斯定理？
贝叶斯定理，就是看着后视镜开车，求看到右转弯灯时在十字路口的概率。


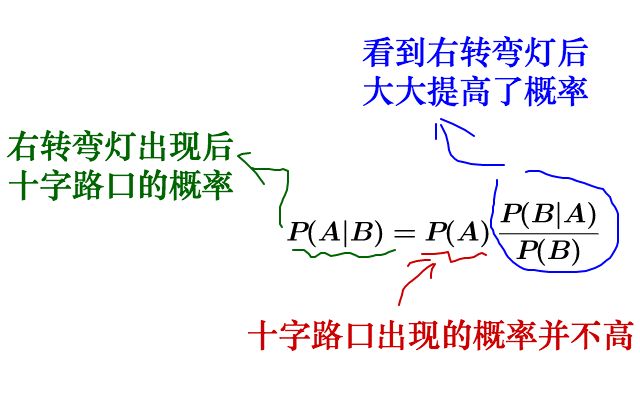
看着后视镜开车，肯定常常会撞车，没关系，我们可以不断的去修正我们的假设。
比如，撞了几次车之后，就发现可能之前估计的在十字路口打右转弯灯的数据明显偏大了，我们修正之后再继续开车。我们人类的学习，本身也是一个试错的过程。

2.怎样用非数学语言讲解贝叶斯定理（Bayes’s theorem）？ - 猴子的回答 - 知乎

贝叶斯的现实意义：如果我能掌握一个事情的全部信息，我当然可以计算出一个客观概率（古典概率）。但生活中绝大多数决策面临的信息都是不全的，我们需要在信息有限的情况下，尽可能做出一个好的预测。也就是，在主观判断的基础上，先估计一个值（先验概率），然后再根据观察到的新信息不断修正（可能性函数），这就是贝叶斯定理利用过去的数据来预测概率的底层思想。

3.通俗易懂！白话朴素贝叶斯—红色石头

如果我对西瓜没有任何了解，包括瓜的颜色、形状、瓜蒂是否脱落。按常理来说，西瓜成熟的概率大概是 60%。那么，这个概率 P(瓜熟) 就被称为先验概率。

也就是说，先验概率是根据以往经验和分析得到的概率，先验概率无需样本数据，不受任何条件的影响。就像只根据常识而不根据西瓜状态来判断西瓜是否成熟，这就是先验概率。

如果我在以前学到了一个判断西瓜是否成熟的常识，就是看瓜蒂是否脱落。一般来说，瓜蒂脱落的情况下，西瓜成熟的概率大一些，大概是 75%。如果把瓜蒂脱落当作一种结果，然后去推测西瓜成熟的概率，这个概率 P(瓜熟 | 瓜蒂脱落) 就被称为后验概率。后验概率类似于执果索因。

知道了先验概率和后验概率，我们再来看看什么是联合概率。买西瓜的例子中，P(瓜熟，瓜蒂脱落) 称之为联合分布，它表示瓜熟了且瓜蒂脱落的概率。关于联合概率，满足下列乘法等式：
$P(瓜熟,瓜蒂脱落)=P(瓜熟|瓜蒂脱落)\cdot P(瓜蒂脱落)=P(瓜蒂脱落|瓜熟)\cdot P(瓜熟)$

如何计算瓜蒂脱落的概率呢？实际上可以分成两种情况：一种是瓜熟状态下瓜蒂脱落的概率，另一种是瓜生状态下瓜蒂脱落的概率。瓜蒂脱落的概率就是这两种情况之和。因此，我们就推导出了全概率公式：

$P(瓜蒂脱落)=P(瓜蒂脱落|瓜熟)\cdot P(瓜熟)+P(瓜蒂脱落|瓜生)\cdot P(瓜生)$

为了买到一个熟瓜，专门在网上搜索了一下，知道判断一个瓜是否熟了，除了要看瓜蒂是否脱落，还要看瓜的形状和颜色。形状有圆和尖之分，颜色有深绿、浅绿、青色之分。现在，特征由原来的 1 个，变成现在的 3 个，我们用 X 表示特征，用 Y 表示瓜的类型（瓜熟还是瓜生）。则根据贝叶斯定理，后验概率 $P(Y=c_k|X=x)$ 的表达式为：

$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)}$

其中，$c_k$ 表示类别，$k$ 为类别个数。本例中，$k$ = 1,2，$c_1$ 表示瓜熟，$c_2$ 表示瓜生。这里的特征 X 不再是单一的，而是包含了 3 个特征。因此，条件概率 $P(X=x|Y=c_k)$ 假设各个条件相互独立，也就是说假设不同特征之间是相互独立的。这样，$P(X=x|Y=c_k)$ 就可以写成：

$P(X=x|Y=c_k)=P(X^1,\cdots ,X^n|Y=c_k)={\Pi }_{j=1}^{n}P(X^j=x^j|Y=c_k)$

其中，n 为特征个数，j 表示当前所属特征。针对这个例子，$P(X=x|Y=c_k)$ 可以写成：

$P(X=x|Y=c_k)=P(X^1=x^1|Y=c_k)P(X^2=x^2|Y=c_k)P(X^3=x^3|Y=c_k)$

这种条件独立性的假设就是朴素贝叶斯法“朴素”二字的由来。这一假设让朴素贝叶斯法变得简单，但是有时候会牺牲一定的分类准确率。

这样，利用朴素贝叶斯思想，我们就可以把后验概率写成：

$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)}=\frac{P(Y=c_k){\Pi }_{j}P(X^j=x^j|Y=c_k)}{{\sum }_{k}P(Y=c_k){\Pi }_{j}P(X^j=x^j|Y=c_k)}$

上式中的分母部分，对于所有的 $c_k$ 来说，都是一样的。因此，分母可以省略，不同的 $c_k$，仅比较 $P(Y=c_k|X=x)$ 的分子即可：

$P(Y=c_k){\Pi }_{j}P(X^j=x^j|Y=c_k)$

直接上例子：
获得了一组包含 10 组样本的数据，当成是历史经验数据，以它为标准。

其中，瓜蒂分为脱落和未脱，形状分为圆形和尖形，颜色分为深绿、浅绿、青色。不同特征组合对应着瓜熟或者瓜生。

现在，挑了一个西瓜，它的瓜蒂脱落、形状圆形、颜色青色。这时候就完全可以根据样本数据和朴素贝叶斯法来计算后验概率。

对于瓜熟的情况：
瓜熟的先验概率： P(瓜熟) = 6 / 10 = 0.6。
条件概率： P(脱落 | 瓜熟) = 4 / 6 = 2 / 3。
条件概率： P(圆形 | 瓜熟) = 4 / 6 = 2 / 3。
条件概率： P(青色 | 瓜熟) = 2 / 6 = 1 / 3。
计算后验概率分子部分：
P(瓜熟) × P(脱落 | 瓜熟) × P(圆形 | 瓜熟) × P(青色 | 瓜熟) = 0.6 × (2 / 3) × (2 / 3) × (1 / 3) = 4 / 45。
对于瓜生的情况：
瓜生的先验概率： P(瓜生) = 4 / 10 = 0.4。
条件概率： P(脱落 | 瓜生) = 1 / 4 = 0.25。
条件概率： P(圆形 | 瓜生) = 1 / 4 = 0.25。
条件概率： P(青色 | 瓜生) = 1 / 4 = 0.25。
计算后验概率分子部分：
P(瓜生) × P(脱落 | 瓜生) × P(圆形 | 瓜生) × P(青色 | 瓜生) = 0.4 × 0.25 × 0.25 × 0.25 = 1 / 160。

因为 4 / 45 > 1 / 160，所以预测瓜蒂脱落、形状圆形、颜色青色的是熟瓜。