大提琴的声音就像一条河，左岸是我无法忘却的回忆，右岸是我值得紧握的璀璨年华，中间流淌的，是我年年岁岁淡淡的感伤。
李白打酒
话说大诗人李白，一生好饮，幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒 2 斗，他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店 mm 次，遇到花 nn 次，已知最后一次遇到的是花，他正好把酒喝光了。
请你计算李白遇到店和花的次序，可以把遇店记为 aa，遇花记为 bb。
例如：这一路上，他一共遇到店 55 次，遇到花 1010 次，已知最后一次遇到的是花，他正好把酒喝光了。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
Input
输入一个整数 TT，包括 TT 组数据，每组数据包括遇到店的次数 mm，花的次数 nn。
Output
对于每组数据，输出李白遇到店和花的可能次序的个数。
Example
input
Copy
1
5 10
output
Copy
14
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
九宫重排
如下面第一个图的九宫格中，放着 1 到 8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。
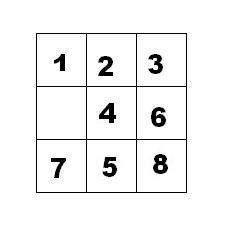我们把第一个图的局面记为：12345678.
把第二个图的局面记为：123.46758
显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出 −1−1。
Input
输入第一行包含九宫的初态，第二行包含九宫的终态。
Output
输出最少的步数，如果不存在方案，则输出 −1−1。
Example
input
Copy
12345678.
123.46758
output
Copy
3
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
两点
福克斯在玩一款手机解迷游戏，这个游戏叫做"两点"。基础级别的时候是在一个 n×mn×m 单元上玩的。像这样：
每一个单元有包含一个有色点。我们将用不同的大写字母来表示不同的颜色。
这个游戏的关键是要找出一个包含同一颜色的环。看上图中 44 个蓝点，形成了一个环。一般的，我们将一个序列 d1,d2,...,dkd1,d2,...,dk 看成一个环，当且仅当它符合下列条件时：
1. 这 kk 个点不一样，即当 i≠ji≠j 时，didi 和 djdj 不同。
2. kk 至少是 44。
3. 所有的点是同一种颜色。
4. 对于所有的 1≤i≤k−11≤i≤k−1: didi 和 di+1di+1 是相邻的。还有 dkdk 和 d1d1 也应该相邻。单元 xx 和单元 yy 是相邻的当且仅当他们有公共边。
当给出一幅格点时，请确定里面是否有环。
Input
单组测试数据。
第一行包含两个整数 nn 和 mm (2≤n,m≤50)(2≤n,m≤50): 板子的行和列。
接下来 nn 行，每行包含一个有 mm 个字母的串，表示当前行每一个点的颜色。每一个字母都是大写字母。
Output
如果有环输出 Yes，否则输出 No。
Example
input
Copy
3 4
AAAA
ABCA
AADA
output
Copy
No
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
大臣的旅费
很久以前，T 王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。
为节省经费，T 国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。
J 是 T 国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。他有一个钱袋，用于存放往来城市间的路费。
聪明的 J 发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第 xx 千米到第 x+1x+1 千米这一千米中（xx 是整数），他花费的路费是 x+10x+10 这么多。也就是说走 11 千米花费 1111，走 22 千米要花费 2323。
J 大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？
Input
输入的第一行包含一个整数 nn (0
城市从 1 开始依次编号，1 号城市为首都
接下来 n−1n−1 行，描述 T 国的高速路（T 国的高速路一定是 n−1n−1 条）
每行三个整数 Pi,Qi,DiPi,Qi,Di，表示城市 PiPi 和城市 QiQi 之间有一条高速路，长度为 DiDi 千米 (0
Output
输出一个整数，表示大臣 J 最多花费的路费是多少
Example
input
Copy
5
1 2 2
1 3 1
2 4 5
2 5 4
output
Copy
135
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
Tri Tiling
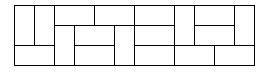
In how many ways can you tile a 3×n3×n rectangle with 2×12×1 dominoes? Here is a sample tiling of a 3×123×12 rectangle.
Input
Input consists of several test cases followed by a line containing −1−1. Each test case is a line containing an integer 0≤n≤300≤n≤30.
Output
For each test case, output one integer number giving the number of possible tilings.
Example
input
Copy
0
6
10
-1
output
Copy
1
41
571
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
01 组成的 N 的倍数
output
standard output
给定一个自然数 N，找出一个 M，使得M>0 且 M 是 N 的倍数，并且 M 的 10 进制表示只包含 0 或 1，求最小的 M。
Input
输入 1个数 N。(1≤N≤106)(1≤N≤106)
Output
输出符合条件的最小的 M。
Examples
input
Copy
1
output
Copy
1
input
Copy
4
output
Copy
100
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
剪格子
如下图所示，3×33×3 的格子中填写了一些整数。
我们沿着图中的星号线剪开，得到两个部分，每个部分的数字和都是 6060。
本题的要求就是请你编程判定：对给定的 m×nm×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割，则输出 00。
Input
程序先读入两个整数 m,nm,n 用空格分割 (m,n<10)(m,n<10)，表示表格的宽度和高度。
接下来是 mm 行，每行 nn 个正整数，用空格分开。每个整数不大于 1000010000。
Output
输出一个整数，表示在所有解中，包含左上角的分割区可能包含的最小的格子数目。
Example
input
Copy
3 3
10 1 52
20 30 1
1 2 3
output
Copy
3
题解：
题目大体意思是要分成两部分，这两部分数字的和要相等。
背后的意思是 怎么分成两部分。
正常思路是 dfs 上下左右，左上角所在集合标记成 1，一旦标记集合的和是总和的一半，此时实现了 “分开”。在每次“分开”中更新最小的块数。
问题来了。（假设阴影处是最优解）
所以 考虑添加方向
变成 8 个方向
int dir[8][2] = {1, 0, 1, -1, 0, 1, 0, -1, -1, 0, -1, 1, 1, 1, -1, -1};
上下左右，左上 左下 右上 右下
但是会有很多组数据超时
最后考虑，斜着的方向只添加一个，左下（从 0, 0 处划分两块，大体方向是左下，下，右下）
int dx[] = {0, 0, 1, -1, 1};
int dy[] = {1, -1, 0, 0, -1};
又出现新问题了
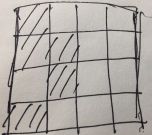
左下角的没有办法剪，所以说：
虽然这种情况可以搜索到，但是这种情况不是解。
怎么排除这种情况呢
被标记的小块的，看看周围有没有提前被标记了的就行了。（上下左右是否接壤）
左下角的上面和右面都没有接壤，所以没有办法剪下来，所以排除。
大体思路就是这样
#include
using namespace std;
const int N = 1e6 + 10;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int n, m;
int ans = INF;
int e[20][20];
int sum; //总和
int dx[] = {0, 0, 1, -1, 1};
int dy[] = {1, -1, 0, 0, -1};
bool vis[20][20];
bool check() { // 检查有没有斜着蹦出来的
int flag = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
if (vis[i][j]) { // 看看所有被标记点 是不是有斜着的
flag = 1;
int k = 0;
for (k = 0; k < 4; k++) {
if (i + dx[k] < 0 || i + dx[k] >= m || j + dy[k] < 0 ||
j + dy[k] >= n)
continue; // 界外
if (vis[i + dx[k]]
[j + dy[k]]) { // 试探： i+dx[k] j+dy[k]
// （上下左右被标记 ） 就跳出
flag = 0;
break; //说明它的上下左右至少有一个接壤的
//也就是说不能出现斜着蹦出来的
}
}
if (flag)
return false;
}
}
return true;
}
void dfs(int x, int y, int res, int step) { // x，y 标记的和，标记了多少块
if (res > sum / 2)
return;
if (res == sum / 2 && check()) {
ans = min(ans, step);
return;
}
for (int i = 0; i <= 4; i++) {
int xx = x + dx[i];
int yy = y + dy[i];
if (xx >= m || yy >= n || xx < 0 || yy < 0)
continue; // 界外
if (!vis[xx][yy]) {
vis[xx][yy] = 1;
dfs(xx, yy, res + e[xx][yy], step + 1);
vis[xx][yy] = 0;
}
}
}
int main() {
scanf("%d%d", &m, &n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
scanf("%d", &e[i][j]), sum += e[i][j];
if (sum & 1) {
printf("0\n");
return 0;
}
vis[0][0] = 1;
dfs(0, 0, e[0][0], 1);
if (ans == INF)
printf("0\n");
else
printf("%d\n", ans);
return 0;
}
