Eigen初始化及基本操作大全

    Eigen常用操作

 
Eigen3安装: ubuntu如何安装Eigen
 

include_directories (/usr/include/Eigen/)

这篇博客主要内容有:

1. Eigen常用头文件
2. Eigen矩阵和向量的基本定义与初始化
3. 高级初始化
     - 行向量RowVectorXd
     - 块赋值
4. 基本运算函数
5. 常用块操作
6. 计算特征值和特征向量
7. Array类, ArrayXf , ArrayXXf
8. 解线性最小二乘
     - 齐次 min||Mx||,分不带约束和带约束条件
     - 非齐次 min||Mx + b||,分不带约束和带约束添加
    

---

1. 常用头文件

#include  //包含了下面的Core/Geometry/LU/Cholesky/SVD/QR/Eigenvalues模块
#include  // 包含Matrix和Array类，基础的线性代数运算和数组操作
#include  // 包含求逆，行列式，LU分解
#include  //包含旋转，平移，缩放，2维和3维的各种变换。
#include  //包含LLT和LDLT Cholesky分解
#include  //包含SVD分解
#include  //包含QR分解
#include  //包含特征值，特征向量分解

#include  //包含稀疏矩阵的存储和运算

#include  //包含Dense和Sparse

2. 基本定义及初始化

Eigen::Matrix<double,2,2> m;
m << 1,2,3,4;

Eigen::MatrixXf m1(2,3);
m1 << 1,2,3,
	  4,5,6;

Eigen::Matrix3d m2 = Eigen::Matrix3d::Identity();//Eigen::Matrix3d::Zero();

Eigen::Matrix3d m3 = Eigen::Matrix3d::Random(); //随机初始化

Eigen::Vector3f v1 = Eigen::Vector3f::Zero();

Eigen::Vector3d v2(1.0, 2.0, 3.0);

Eigen::VectorXf v3(20); //维度为20的向量,未初始化.
v3 << 1.0 , 2.0 , 3.0;

cout << m1(1,1) << endl;
cout << v1(1) << endl;

3. 高级初始化

//1. Eigen::RowVectorXd //行向量,之前的Vector都是列向量
using namespace Eigen;
RowVectorXd rv1(1,2,3);
RowVectorXd rv2(4);
rv2 << 1,2,3,4;
RowVectorXd joined_rv12(7);
joined_rv12 << rv1 , rv2;//rv1后接rv2
//joined_rv12 is:
1 2 3 1 2 3 4;

//2. 块操作
MatrixXf m4(2,2);
m4 << 1,2,3,4;
MatrixXf m5(4,4);
m5 << m4, m4 / 10, m4 * 10, m4;//将m5分了四块赋值
//m5 is :
1  2  0.1 0.2 
3  4  0.3 0.4
10 20  1   2
30 40  3   4

Matrix3f m6;
m6.row(0) << 1,2,3;
m6.block(1,0,2,2) << 4,5,6,7; //
//m6.block<2,2>(1,0) << 4,5,6,7;
m6.col(2).tail(2) << 6,9;
//m6 is: 
1 2 3
4 5 6
6 7 9

3. 基本运算函数

MatrixXf m7 = MatrixXf::Random(3,3);
m7.row(i);//矩阵第i行
m7.col(j);//矩阵第j列
m7.transpose();
m7.conjugate();//共轭
m7.adjoint(); //共轭转置
m7.minCoeff();//所有元素中最小元素
m7.maxCoeff();//所有元素中最大元素
m7.trace();//迹，对角元素的和
m7.sum(); //所有元素求和
m7.prod(); //所有元素求积
m7.mean(); //所有元素求平均

Vector3f v4(4,5,6);
Vector3f v5(7,8,9);
v4.dot(v5); //点乘
v4.cross(v5);//叉乘

/** 矩阵的+、-、数×、乘法
左右两侧变量具有相同的尺寸（行和列），并且元素类型相同（Eigen不自动转化类型），
其运算和int,float等基本类型相同。*/
Vector3f v6 = m7 * v5;
Matrix3f m_sum = m6 + m7;
Matrix3f m_dec = m6 - m7;
Matrix3f m_prod = 2.5 * m7;
Matrix3f m_prod2 = m6 * m7;
Matrix3d m_dev = m7 / 2.0;

4. 常用块操作

MatrixXd m8 = MatrixXd::Random(3,3);

//① 行列
m8.row(i);
m8.col(j);

//② block<>()
Matrix<double,p,q> m9 = m8.block(i,j,p,q);//起点(i, j)，块大小(p, q)，构建一个动态尺寸的block
m8.block<p,q>(i,j);

③ Matrix其他块操作

④ Vector块操作

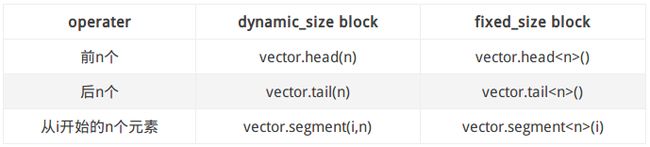
注: ③ ④中的图,引用了大佬的博客:Eigen库使用指南
 

5.计算特征值和特征向量

Eigen::MatrixXd m9 = Eigen::MatrixXd::Random(3,3);
Eigen::MatrixXd mTm = m9.transpose() * m9;

Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(mTm);
Eigen::VectorXd eigenvalues = eigen_solver.eigenvalues();
Eigen::MatrixXd eigenvectors = eigen_solver.eigenvectors();
Eigen::VectorXd v0 = eigenvectors.col(0);// 因为特征值一般按从小到大排列,所以col(0)就是最小特征值对应的特征向量

6. Array类

 Eigen中的Array类,定义了许多Matrix和Vector类没有的运算,比如矩阵和标量的加减运算,Array和Matrix之间也容易相互转换.

6.1 Array的初始化和访问

//定义
typedef Array<float ,Dynamic,1>  ArrayXf;
typedef Array<float,3,1>         Array3f;
typedef Array<double,Dynamic ,Dynamic > ArrayXXd;
typedef Array<double ,3,3 >    Array33d;

//初始化   没有Eigen::Array33f::Identity();
Eigen::Array33f a1 = Eigen::Array33f::Zero();
Eigen::ArrayXf a2 = Eigen::ArrayXf::Zero(3);
Eigen::ArrayXXf a3 = Eigen::ArrayXXf::Zero(3,4);
Eigen::Array33f a3 = Eigen::ArrayXXf::Zero();

Eigen::ArrayXXf a4(2,2);
a4 << 1,2,3,4;

//访问
cout << a4(0,0) << endl;

6.2 Array高级初始化

ArrayXXf a5(10, 4);
a5.col(0) = ArrayXf::LinSpaced(10, 0, 90);//间隔10,从0到90赋值
a5.col(1) = M_PI / 180 * a5.col(0);
a5.col(2) = a5.col(1).sin();//对a5的第一列,用sin()求值后赋值给a5.col(2)对应每一个位置
a5.col(3) = a5.col(1).cos();//求cos
std::cout << " Degrees Radians Sine Cosine\n";
std::cout << a5 << std::endl;

输出为:

//output
Degrees Radians Sine Cosine
           0            0            0            1
          10     0.174533     0.173648     0.984808
          20     0.349066      0.34202     0.939693
          30     0.523599          0.5     0.866025
          40     0.698132     0.642788     0.766044
          50     0.872665     0.766044     0.642788
          60       1.0472     0.866025          0.5
          70      1.22173     0.939693      0.34202
          80      1.39626     0.984808     0.173648
          90       1.5708            1      -4.37114e-08

参考博客地址: eigen中高级初始化
 

7. 解线性最小二乘方程

7.1 齐次线性最小二乘 min||Mx||,M是4 * 4矩阵

(1) 无约束条件: $min||Mx||$
 - 理论上：取MTM的最小特征值对应的特征向量作为x的解；
 - 工程上：对M做svd分解，$M=U\Sigma V^T$,取最小奇异值对应的V的列向量作为x的解（实际上，奇异值一般按由大到小排列，V的最后一列就是解）,证明:证明AX=0的最小二乘解是ATA最小特征值对应的特征向量
 - 求解方法有两种:特征向量分解 和 svd分解
 
  - 注意,对于MX = 0的问题,做分解的时候,一般会变成$M^{T}MX=0$.
  - 注意,要先判别矩阵的病态性,如果条件数太大,表示病态严重,则结果精度很低

//1. 特征值和特征向量分解
Eigen::JacobiSVD<Eigen::MatrixXd> svd(MTM);
//条件数等于最小的奇异值除以最小的奇异值
double cond = svd.singularValues()(0) / svd.singularValues()(svd.singularValues().size() - 1);
if (cond > max_cond_number)//max_cond_number: 自己设置的条件数阈值,我设置的是75
{
  std::cout << colouredString("Matrix A is almost singular.", RED, BOLD) << std::endl;
  return 0;
}
  
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(MTM);
Eigen::VectorXd eigenvalues = eigen_solver.eigenvalues();
Eigen::MatrixXd eigenvectors = eigen_solver.eigenvectors();
Eigen::VectorXd X = eigenvectors.col(0);// 因为特征值一般按从小到大排列,所以col(0)就是最小特征值对应的特征向量

//2. svd分解
Eigen::JacobiSVD<Eigen::MatrixXd> svd(MTM, Eigen::ComputeFullU |Eigen::ComputeFullV);
//Eigen::VectorXd singular_values = svd.singularValues();
//Eigen::MatrixXd singular_matrix = svd.matrixV();
Eigen::Vector3d X = svd.matrixV().block<4,1>(0,3);// 因为奇异值一般按从大到小排列,所以,最后一列就是最小奇异值对应的向量.

(2) 带约束条件: $min||MX||,X[0]\ast X[3]=X[1]\ast X[2],||X||=1$;
  - 有n约束,就取最小的n个列向量,乘以n个系数,然后用n个约束去求解n个系数,就是方程的最小二乘解.
     $X=a\ast V_1+b\ast V_2$

Eigen::JacobiSVD<Eigen::MatrixXd> svd(MTM, Eigen::ComputeFullU |Eigen::ComputeFullV);
Eigen::Vector3d V1 = svd.matrixV().block<4,1>(0,3);
Eigen::Vector3d V2 = svd.matrixV().block<4,1>(0,2);
//再求a 和 b, X = a*V1 + b*V2

7.2 非齐次线性最小二乘 min||Mx - b||

(1) 不带约束条件
  - 采用奇异值分解;
  - 注意,要先判别矩阵的病态性,如果条件数太大,表示病态严重,则结果精度很低

  Eigen::JacobiSVD<Eigen::MatrixXd> svd(M);
  double cond = svd.singularValues()(0) / svd.singularValues()(svd.singularValues().size() - 1);
  //std::cout << "cond "  << cond << std::endl;
  if (cond > max_cond_number)//max_cond_number: 自己设置的条件数阈值,我设置的是75
  {
    std::cout << colouredString("Matrix A is almost singular.", RED, BOLD) << std::endl;
    return 0;
  }

  Eigen::VectorXd X = Eigen::Vector2d::Zero();
  X = M.colPivHouseholderQr().solve(b);

  - 除了colPivHouseholderQr()分解,还有:

 
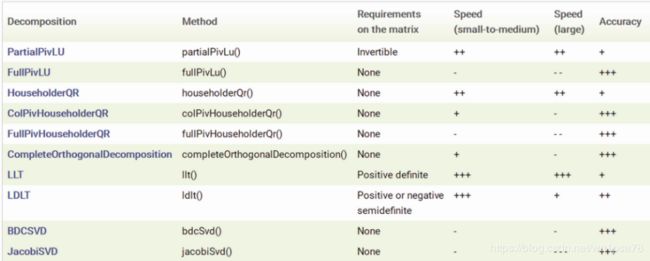
(2) 带约束条件
  - 拉格朗日数乘法,请参考论文中的部分求解:Simultaneous Calibration of Odometry and Parameters for Mobile Robots
  - 采用非线性优化的方法(需要较好的初始值,需要合理的权重)