【leetcode】42 接雨水（栈，双指针）

题目链接：https://leetcode-cn.com/problems/trapping-rain-water/

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

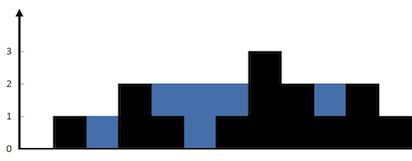
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

思路

1 暴力

对于数组中的每个元素，找到下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值

复杂度分析

• 时间复杂度：O（n^2）
• 空间复杂度：O（1）

class Solution {
public:
    int trap(vector<int>& height) {
        int ret = 0;
        int len = height.size();
        for (int i = 1; i < len -1; ++i) {
            int maxLeft = height[i], maxRight = height[i];
            for (int j = i-1; j >=0 ; --j)
                maxLeft = max(maxLeft,height[j]);       // 找到左边最大值
            for (int j = i+1; j < len;++j)
                maxRight = max(maxRight,height[j]);     // 找到右边最大值
            ret += min(maxLeft,maxRight) - height[i];   // 两边最大高度的较小值减去当前高度的值
        }
        return ret;
    }
};

2 动态编程

在暴力方法中，我们仅仅为了找到最大值每次都要向左和向右扫描一次。但是我们可以提前存储这个值。因此，可以通过动态编程解决。

提前存储每个元素左边最大值和右边最大值。

复杂度分析

• 时间复杂度：O（n）
• 空间复杂度：O（n）

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size() < 3)
            return 0;
        int ret = 0;
        int len = height.size();
        vector<int> maxLeft(len,0), maxRgiht(len,0);
        maxLeft[0] = height[0], maxRgiht[len-1] = height[len-1];
        for (int i = 1; i < len; ++i)
            maxLeft[i] = max(maxLeft[i-1], height[i]);
        for (int i = len-2; i>=0 ; --i)
            maxRgiht[i] = max(maxRgiht[i+1], height[i]);
        for (int i = 0; i < len; ++i)
            ret += min(maxLeft[i], maxRgiht[i]) - height[i];
        return ret;
    }
};

3 递减栈

我们可以不用像方法 2 那样存储最大高度，而是用栈来跟踪可能储水的最长的条形块。使用栈就可以在一次遍历内完成计算。

我们在遍历数组时维护一个栈。如果当前的条形块小于或等于栈顶的条形块，我们将条形块的索引入栈，意思是当前的条形块被栈中的前一个条形块界定。如果我们发现一个条形块长于栈顶，我们可以确定栈顶的条形块被当前条形块和栈的前一个条形块界定，因此我们可以弹出栈顶元素并且累加答案到 ret 。

4 双指针

和方法 2 相比，我们不从左和从右分开计算，我们想办法一次完成遍历。 从动态编程方法的示意图中我们注意到，只要 right_max[i]>left_max[i] （元素 0 到元素 6），积水高度将由 left_max 决定，类似地 left_max[i]>right_max[i]（元素 8 到元素 11）。

所以我们可以认为如果一端有更高的条形块（例如右端），积水的高度依赖于当前方向的高度（从左到右）。当我们发现另一侧（右侧）的条形块高度不是最高的，我们则开始从相反的方向遍历（从右到左）。 我们必须在遍历时维护 left_max 和 right_max ，但是我们现在可以使用两个指针交替进行，实现 1 次遍历即可完成。

注意：while里的判断条件if (height[left] < height[right]) 控制了如果左边有较大的值，则当前雨水量取决于右边最大值！

复杂度分析：

• 时间复杂度：O(n)。单次遍历的时间O(n)。
• 空间复杂度：O(1) 的额外空间。

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size() < 3)
            return 0;
        int ret = 0;
        int maxLeft = 0, maxRight = 0;
        int left = 0, right = height.size() -1;
        while(left < right){
            if (height[left] < height[right]){     
                if (height[left] > maxLeft)
                    maxLeft = height[left];
                else
                    ret += maxLeft - height[left];
                ++ left;
            }else{
                if (height[right] > maxRight)
                    maxRight = height[right];
                else
                    ret += maxRight - height[right];
                -- right;
            }
        }

        return ret;
    }
};