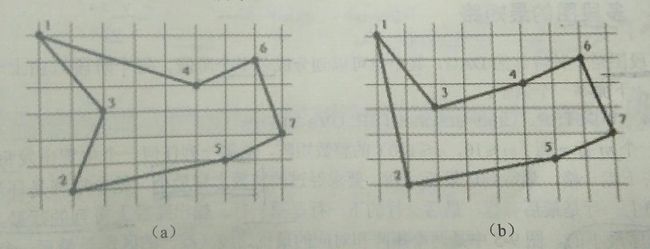UVA 1347 Tour(旅行(算法竞赛入门经典——例题9-3))(翻译,详解)
Tour
John Doe, a skilled pilot, enjoys traveling. While on vacation, he rents a small plane and starts visitingbeautiful places. To save money, John must determine the shortest closed tour that connects hisdestinations. Each destination is represented by a point in the plane pi =< xi, yi >. John uses thefollowing strategy: he starts from the leftmost point, then he goes strictly left to right to the rightmostpoint, and then he goes strictly right back to the starting point. It is known that the points havedistinct x-coordinates.Write a program that, given a set of n points in the plane, computes the shortest closed tour thatconnects the points according to John’s strategy.
给定平面上n(n<=1000)个点的坐标(按照x递增的顺序给出。各点x坐标不同,且均为正整数),你的任务是设计一条路线,从最左边的点出发,走到最右边的点后再返回,要求除了最左点和最右点之外每个点恰好经过一次,且路径总长度最短。两点间的长度为它们的欧几里得距离(在此是二维空间上的两点的距离),如图所示:
Input
The program input is from a text file. Each data set in the file stands for a particular set of points. Foreach set of points the data set contains the number of points, and the point coordinates in ascendingorder of the x coordinate. White spaces can occur freely in input. The input data are correct.
Output
For each set of data, your program should print the result to the standard output from the beginningof a line. The tour length, a floating-point number with two fractional digits, represents the result.
Note: An input/output sample is in the table below. Here there are two data sets. The first onecontains 3 points specified by their x and y coordinates. The second point, for example, has the xcoordinate 2, and the y coordinate 3. The result for each data set is the tour length, (6.47 for the firstdata set in the given example).
Sample Input
3
1 1
2 3
3 1
4
1 1
2 3
3 1
4 2
Sample Output
6.47
7.89
思路:
“从左到右再回来”不太方便思考,可以改成:两个人同时从最左点出发,沿着两条不同的路径走,最后都走到最右点,且除了起点和终点外其余每个点恰好被一个人经过。这样就可以用dp[i][j]表示第一个人走到i,第二个人走到j,还需要走多长的距离。
状态如何转移呢?仔细思考后会发现:好像很难保证两个人不会走到相同的点。例如,计算状态d[i][j]的时,能不能让i走到i+1呢?不知道,因为从状态里看不出来i+1有没有被j走过。换句话说,状态定义得不好,导致转移困难。
下面修改一下:dp[i][j]表示1~max(i,j)全部走过,且两个人的当前位置分别是i和j,还需要走多长的距离。不难发现dp[i][j]=dp[j][i],因此从现在开始规定在状态中i>j。这样,不管是哪个人,下一步只能走到i+1,i+2,...这些点。可是,如果走到i+2,情况变成了“1~i和i+2,但是i+1没走过”,无法表示成状态!怎么办?禁止这种决策!也就是说,只允许其中一个人走到i+1(并且一定要有一个人走到i+1,这样才不会漏解),而不能走到i+2,i+3,...。换句话说,状态dp[i][j]只能转移到dp[i+1][j](第一个人走到i+1)或dp[i+1][i](第二个人走到i+1时本应转移到dp[i][i+1],但是根据此处规定(规定状态dp[i][j]中i>j),必须写成d[i+1][i])。
可是这样做产生了一个问题,上述“霸道”的规定是否可能产生漏解呢?不会。因为如果第一个人直接走到了i+2,那么它再也无法走到i+1了,只能靠第二个人走到i+1。既然如此,现在就让第二个人走到i+1,并不会丢失解(即一定有一个人要走下一步i+1)。
边界是d[n-1][j]=dis[n-1][n]+dis[j,n],其中dis[a][b]表示点a和点b之间的距离。因为根据定义,所有点都走过了,两个人只需直接走到终点。所求结果是dis[1][2]+dp[2][1],因为第一步是某个人走到了第二个点,根据定义这就是dp[2][1]。
状态总数有O(n^2)个每个状态的决策只有两个,因此总时间复杂度为O(n^2)。
AC代码:
递推写法:
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
double dp[1005][1005];//dp[i][j]表示两个人当前位置分别是i,j,最少还需要走多长的距离 ,且设定i>j,表示i之前的点都走过了
int n;
struct node
{
double x,y;
}map[1005];
double dis(int i,int j)//求点i,j之间的距离
{
return sqrt((map[i].x-map[j].x)*(map[i].x-map[j].x)+(map[i].y-map[j].y)*(map[i].y-map[j].y));
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
scanf("%lf %lf",&map[i].x,&map[i].y);
for(int i=1;i<=n-1;i++)
dp[n-1][i]=dis(n-1,n)+dis(i,n);
for(int i=n-2;i>1;i--)
for(int j=1;jj
dp[i][j]=min(dp[i+1][j]+dis(i,i+1),dp[i+1][i]+dis(i+1,j));
printf("%.2lf\n",dis(1,2)+dp[2][1]);
}
return 0;
}
递归写法:
#include
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
double dp[1005][1005];//dp[i][j]表示两个人当前位置分别是i,j,最少还需要走多长的距离 ,且i>j,i之前的点都走过了
int n;
struct node
{
double x,y;
}map[1005];
double dis(int i,int j)//求点i,j之间的距离
{
return sqrt((map[i].x-map[j].x)*(map[i].x-map[j].x)+(map[i].y-map[j].y)*(map[i].y-map[j].y));
}
double getdp(int i,int j)
{
if(dp[i][j]>0) return dp[i][j];
return dp[i][j]=min(dis(i,i+1)+getdp(i+1,j),dis(j,i+1)+getdp(i+1,i));
}
int main()
{
while(~scanf("%d",&n))
{
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++)
scanf("%lf %lf",&map[i].x,&map[i].y);
for(int i=1;i<=n-1;i++)
dp[n-1][i]=dis(n-1,n)+dis(i,n);
printf("%.2lf\n",getdp(1,1));
//printf("%.2lf\n",dis(1,2)+getdp(2,1));
}
return 0;
}