Educational Codeforces Round 57 (Rated for Div. 2)

A. Find Divisible

Description:

You are given a range of positive integers from $l$ to $r$.
Find such a pair of integers $(x,y)$ that $l\le x,y\le r$, $x̸=y$ and $x$ divides $y$.
If there are multiple answers, print any of them.
You are also asked to answer $T$ independent queries.

Input:

The first line contains a single integer $T$ ($1\le T\le 1000$) — the number of queries.
Each of the next $T$ lines contains two integers $l$ and $r$ ($1\le l\le r\le 998244353$) — inclusive borders of the range.
It is guaranteed that testset only includes queries, which have at least one suitable pair.

Output:

Print $T$ lines, each line should contain the answer — two integers $x$ and $y$ such that $l\le x,y\le r$, $x̸=y$ and $x$ divides $y$. The answer in the $i$-th line should correspond to the $i$-th query from the input.
If there are multiple answers, print any of them.

Sample Input:

3
1 10
3 14
1 10

Sample Output:

1 7
3 9
5 10

题目链接

在区间 $l$ 到 $r$ 内找到两个数使得第一个数是第二个数的因子，题目保证有解。

因为题目保证有解且输出的两个数又不能相等，所以最小倍数即为 $2$ ，直接输出 $l$ 及 $2\times l$ 即可。

AC代码:

#include
using namespace std;

int T;
int L, R;

int main(int argc, char *argv[]) {
    scanf("%d", &T);
    for (int Case = 1; Case <= T; ++Case) {
        scanf("%d%d", &L, &R);
        printf("%d %d\n", L, L * 2);
    }
    return 0;
}

B. Substring Removal

Description:

You are given a string $s$ of length $n$ consisting only of lowercase Latin letters.
A substring of a string is a contiguous subsequence of that string. So, string “forces” is substring of string “codeforces”, but string “coder” is not.
Your task is to calculate the number of ways to remove exactly one substring from this string in such a way that all remaining characters are equal (the number of distinct characters either zero or one).
It is guaranteed that there is at least two different characters in $s$.
Note that you can remove the whole string and it is correct. Also note that you should remove at least one character.
Since the answer can be rather large (not very large though) print it modulo $998244353$.
If you are Python programmer, consider using PyPy instead of Python when you submit your code.

Input:

The first line of the input contains one integer $n$ ($2\le n\le 2\cdot 10^5$) — the length of the string $s$.
The second line of the input contains the string $s$ of length $n$ consisting only of lowercase Latin letters.
It is guaranteed that there is at least two different characters in $s$.

Output:

Print one integer — the number of ways modulo $998244353$ to remove exactly one substring from $s$ in such way that all remaining characters are equal.

Sample Input:

4
abaa

Sample Output:

6

Sample Input:

7
aacdeee

Sample Output:

6

Sample Input:

2
az

Sample Output:

3

题目链接

从 $n$ 个字符的字符串中去除一段连续区间使得字符串有且仅有一种字符。

找到左右第一个不同的字符位置组合计数即可。

AC代码:

#include
using namespace std;

const int mod = 998244353;
const int maxn = 2e5 + 5;

long long QuickMul(long long A, long long B) {
    long long Ans = 0;
    while (B) {
        if (B & 1) {
            Ans = (Ans + A) % mod;
        }
        A = (A + A) % mod;
        B >>= 1;
    }
    return Ans;
}

int N;
char Str[maxn];
long long Left, Right;

int main(int argc, char *argv[]) {
    scanf("%d%s", &N, Str + 1);
    int Left = 1, Right = N;
    for (int i = 2; i <= N; ++i) {
        if (Str[i] != Str[i - 1]) {
            Left = i;
            break;
        }
    }
    for (int i = N - 1; i >= 1; --i) {
        if (Str[i] != Str[i + 1]) {
            Right = i;
            break;
        }
    }
    Right = (N - Right) + 1;
    if (Str[1] == Str[N]) {
        printf("%lld\n", QuickMul(Left, Right));
    }
    else {
        printf("%lld\n", ((Left + Right) % (long long)mod - 1 * 1LL + (long long)mod) % (long long)mod);
    }
    return 0;
}

C. Polygon for the Angle

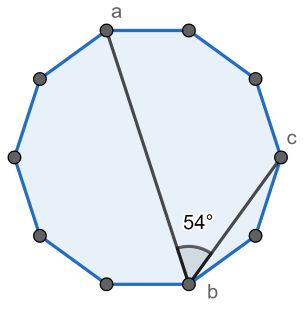
Description:

You are given an angle $\text{ang}$.
The Jury asks You to find such regular $n$-gon (regular polygon with $n$ vertices) that it has three vertices $a$, $b$ and $c$ (they can be non-consecutive) with $\angle abc=\text{ang}$ or report that there is no such $n$-gon.

If there are several answers, print the minimal one. It is guarantied that if answer exists then it doesn’t exceed $998244353$.

Input:

The first line contains single integer $T$ ($1\le T\le 180$) — the number of queries.
Each of the next $T$ lines contains one integer $\text{ang}$ ($1\le \text{ang}<180$) — the angle measured in degrees.

Output:

For each query print single integer $n$ ($3\le n\le 998244353$) — minimal possible number of vertices in the regular $n$-gon or $-1$ if there is no such $n$.

Sample Input:

4
54
50
2
178

Sample Output:

10
18
90
180

题目链接

求正多边形任意三顶点连线内角为 $n$ 的最小多边形边数。

多边形外角和为 $360°$ 可由此计算出正 $n$ 边形一个内角为 $180-\frac{360}{n}$ ,将正多边形其中一个顶点与其余所有顶点连线，其内角被连线平分（正多边形可外接圆，其每个角均为圆周角，弧长相等则角度相等） ，所以可以计算出其最小的角度为 $\frac{180-\frac{360}{n}}{n-2}$ ，判断此角度能否整除输出角度 $ang$ 即可（注意判断其内角最大为 $180-\frac{360}{n}$）。

AC代码:

#include
using namespace std;

const int maxn = 998244353;

int T;
int Ang;
int Angle;
int Data[185];

void Init() {
    for (int i = 1; i <= 179; ++i) {
        for (int j = 3; j <= maxn; ++j) {
            if (360 % j != 0) {
                continue;
            }
            Angle = (180 - 360 / j);
            if (Angle == i) {
                Data[i] = j;
                break;
            }
            if (Angle % (j - 2) != 0 || Angle < i) {
                continue;
            }
            Angle /= (j - 2);
            if (i % Angle == 0) {
                Data[i] = j;
                break;
            }
        }
        if (Data[i] == 0) {
            Data[i] = -1;
        }
    }
    Data[180] = -1;
}

int main(int argc, char *argv[]) {
    Init();
    scanf("%d", &T);
    for (int Case = 1; Case <= T; ++Case) {
        scanf("%d", &Ang);
        printf("%d\n", Data[Ang]);
    }
    return 0;
}

D. Easy Problem

Description:

Vasya is preparing a contest, and now he has written a statement for an easy problem. The statement is a string of length $n$ consisting of lowercase Latin latters. Vasya thinks that the statement can be considered hard if it contains a subsequence hard; otherwise the statement is easy. For example, hard, hzazrzd, haaaaard can be considered hard statements, while har, hart and drah are easy statements.
Vasya doesn’t want the statement to be hard. He may remove some characters from the statement in order to make it easy. But, of course, some parts of the statement can be crucial to understanding. Initially the ambiguity of the statement is $0$, and removing $i$-th character increases the ambiguity by $a_i$ (the index of each character is considered as it was in the original statement, so, for example, if you delete character r from hard, and then character d, the index of d is still $4$ even though you delete it from the string had).
Vasya wants to calculate the minimum ambiguity of the statement, if he removes some characters (possibly zero) so that the statement is easy. Help him to do it!
Recall that subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements.

Input:

The first line contains one integer $n$ ($1\le n\le 10^5$) — the length of the statement.
The second line contains one string $s$ of length $n$, consisting of lowercase Latin letters — the statement written by Vasya.
The third line contains $n$ integers $a_1,a_2,\dots ,a_n$ ($1\le a_i\le 998244353$).

Output:

Print minimum possible ambiguity of the statement after Vasya deletes some (possibly zero) characters so the resulting statement is easy.

Sample Input:

6
hhardh
3 2 9 11 7 1

Sample Output:

5

Sample Input:

8
hhzarwde
3 2 6 9 4 8 7 1

Sample Output:

4

Sample Input:

6
hhaarr
1 2 3 4 5 6

Sample Output:

0

题目链接

长度为 $n$ 的字符串每个字符都有其消除花费权值，使用最小的花费消除字符使字符串中不存在hard(非必须连续)

考虑动态规划，对于字符a来说转移方程为：$dp[i][1]=min(dp[i-1][0],dp[i][1]+cost[i])$ （其中 $i$ 为遍历字符索引位置）， $dp[i-1][0]$ 是把 $i$ 位置之前(不包括 $i$ )的字符h全部清除， $dp[i][1]+cost[i]$ 是把 $i$ 位置之前(包括 $i$ )的字符a全部清除，两者取最小值即可，其余字符r、d同理。

AC代码:

#include
using namespace std;

const int maxn = 1e5 + 5;

int N;
char Str[maxn];
long long Cost[maxn];
long long Dp[maxn][4];

int main(int argc, char *argv[]) {
    scanf("%d%s", &N, Str + 1);
    for (int i = 1; i <= N; ++i) {
        scanf("%lld", &Cost[i]);
    }
    for (int i = 1; i <= N; ++i) {
        for (int j = 0; j < 4; ++j) {
            Dp[i][j] = Dp[i - 1][j];
        }
        if (Str[i] == 'h') {
            Dp[i][0] += Cost[i];
        }
        else if (Str[i] == 'a') {
            Dp[i][1] = min(Dp[i - 1][0], Dp[i][1] + Cost[i]);
        }
        else if (Str[i] == 'r') {
            Dp[i][2] = min(Dp[i - 1][1], Dp[i][2] + Cost[i]);
        }
        else if (Str[i] == 'd') {
            Dp[i][3] = min(Dp[i - 1][2], Dp[i][3] + Cost[i]);
        }
    }
    printf("%lld\n", min(Dp[N][0], min(Dp[N][1], min(Dp[N][2], Dp[N][3]))));
    return 0;
}