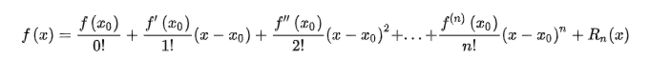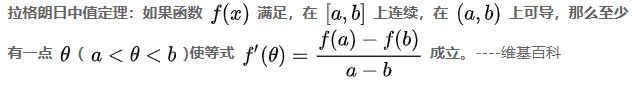1、为什么要学泰勒公式?
泰勒公式刚碰到时,总觉得一头雾水,一大串数字,把一个简简单单的初等函数描述出来,这样岂不是很复杂?在进一步理解泰勒公式之后,我觉得泰勒公式还是非常有用的,单单就我个人认为,当然涉及到其它许多领域也有它的身影,只不过就笔者一个备考的人来说,目前只认识到他在数学方面上的意义而已。
比如我们通常认识的sinx,e^x,cosx,tanx。这些初等函数似乎很简单,但是不要忘了,我们从初中以来,只会计算它的一些特殊角的值,比如30,0,60度这些特殊角,后来进一步学了更深层次的sin2x,cos2x,使我们可以计算15,105度诸如此类的特殊角,相比初中时期的我们来说,我们有所进步,但是对于角度为2,3,4这些等等的更具一般意义的角度我们就熟手无策了!
这个时候泰勒公式就出现了,泰勒公式的思想就在于:用多项式去拟合一个函数图像(说白了就是拿这些多项式去近似代表一个函数),就拿e^x,sinx这些来说,可以通过一些简简单单的,带有不同系数的幂函数进行累加表示。
2、泰勒公式
(1)泰勒公式:
(相应的,X0=0时,称为麦克劳林公式)
麦克劳林公式:
就像上面的这个式子所示,它只涉及到了简单的幂函数的加和运算,就把一些抽象的初等函数,诸如sinx,cosx,e^x,转化为泰勒公式的形式(幂函数求和),这在电脑编程也化抽象为具体,容易实现。
这里给出泰勒公式的各项系数的推导:
此处的C就是系数,我们通过推导,可以知道,泰勒公式的每个系数都与原函数的导数有关,即我们的多项式的各阶导数都与原函数相同,这样我们拟合的函数就可以近似代表原函数了。
(2)对应的例子:
下面均用麦克劳林公式举例,因为麦克劳林公式,是X0=0,即泰勒公式的特殊形式。特殊形式更容易理解,理解完特殊形式,再思考一般形式就比较好理解了。
先来说一下,幂函数的和(即多项式求和)为什么可以去表示任何一个函数。
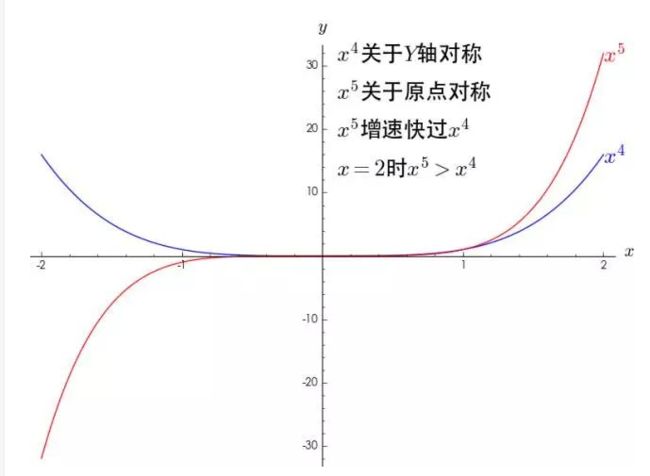
《1》先看两幅图:
上面两幅图,实际上说明了,所有幂函数都只有两种形式,一种是关于y对称,另一种是关于原点对称。
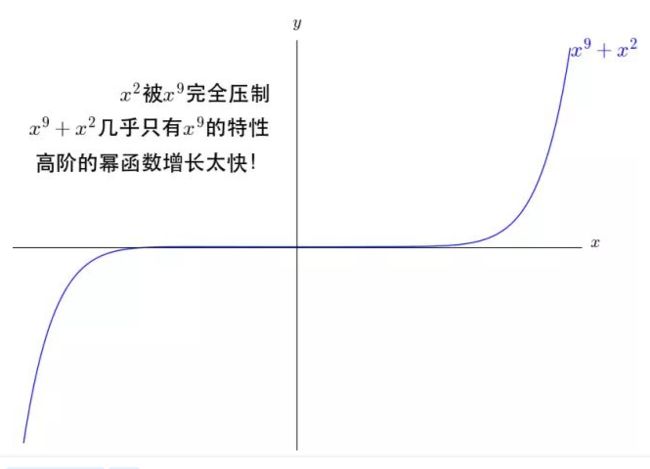
《2》继续看两幅图
这里可以看出,比较高次的幂函数,总体上远远超过低次函数的变化程度。当两个系数一致,次数不同的幂函数相加时,低次函数总会被压制。
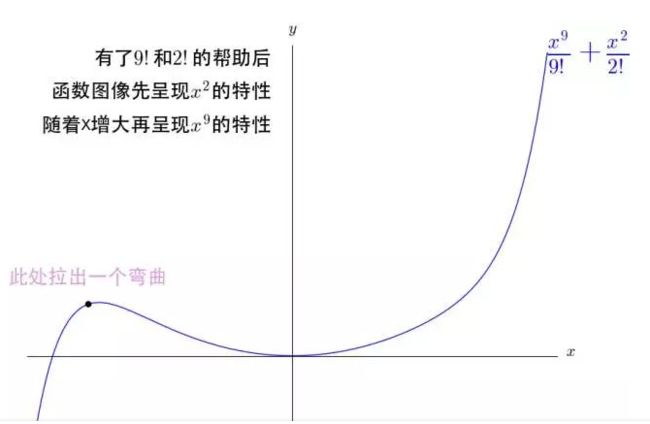
这里可以看出,通过改变系数,不同次数的幂函数图像会先呈现低次幂函数的特性,再随着X变量增大,呈现高次幂函数的特性。
拿e^x通过麦克劳林(在0处展开的泰勒公式)展开看看:
可以看到展开的项越多,越精确。
再看看sinx
随着项数的增加也是越来越靠近。
总结:
(1)上面的图像都是麦克劳林公式展开的情况。也就是泰勒公式在0处展开。一般的,我们可以在任意位置张开,即f(X),X取任意值,得到一般的泰勒公式。
(2)泰勒公式在用于求函数值的时候,即X趋近于某个数时,拟合效果(近似效果还是挺好的),拿考研举例,一般是用于求函数在自变量趋于某个数的值,此时使用泰勒公式求得的值就行带入就很准确;
(3)如果泰勒公式在拟合一些比较变态的函数图像,必须保证展开的n次项足够大,在一定范围内才能准确表示。
3.泰勒公式的误差
上面说了很多泰勒公式的项,却没说到误差,因为泰勒公式我们主要用来近似一个函数,所以误差就是公式后面的 Rn(X)。
它怎么计算呢?
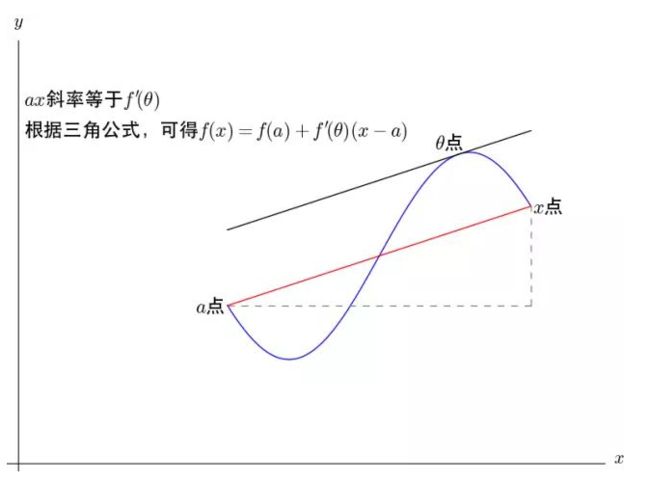
<1>先看看拉格朗日中值定理:
说白了就是,有一个函数f(X)在【a,b】连续,(a,b)上可导,那么把a,b连起来,直线ab的斜率k,在【a,b】区域内可以找到一个导数,使得这个导数 f'(x)=k
类似的当扩大项数时,误差为:
再加一点。
到这里就完结了。
我真的是对比先人望尘莫及,先人可以想到这么棒的方法,我单单是理解,学着用就死了多少脑细胞了……