AC自动机粗略解析

AC自动机解决的问题是，多个单词在一篇文章中出现频率的多对一类的问题。

解决问题的步骤是：1、建立Trie树；2、构造失败指针；3、模式匹配。

构造失败指针是关键步骤，能够降低匹配的复杂度，有类似于KMP算法中next[]数组的作用，只是比next[]在匹配时要麻烦一点，但是可以先预处理出next数组。失败指针，顾名思义，即在匹配失败的时候下一步的位置，如果不用AC自动机，则会回溯到根节点，这样必然是不明♂智的。可以利用的队列建立失败指针。

相关操作如下：

queue  q;

void BuildACAutomation(TrieNode *root) {
    TrieNode *cur, *ptr;

    root->fail = NULL;

    q.push(root);

    while (!q.empty()) {
        cur = q.front(); 

        q.pop();

        for (int i = 0; i//build *fail for cur's children ie.next[i]

            if (cur->next[i] != NULL) { 
                //*cur has i-th child

                ptr = cur->fail;
                //*ptr point to father's *fail
                //cur->next[i]'s *fail may be point to cur's *fail's son

                while (ptr && ptr->next[i] == NULL) ptr = ptr->fail;
                //until has a son

                if (ptr == NULL) cur->next[i]->fail = root; 
                //*ptr point to root's *fail

                else cur->next[i]->fail = ptr->next[i]; 
                //cur's *fail has i-th child

                q.push(cur->next[i]);
            }
        }
    }//end while
}

int query(char x[], TrieNode *root) {
    int i = 0, res = 0, idx;

    TrieNode *cur = root, *ptr;

    while (x[i]) {
        idx = x[i] - 'a';

        while (cur != root && cur->next[idx] == NULL)
            cur = cur->fail; 
            //to find the first

        cur = cur->next[idx];

        if (cur == NULL) cur = root; 
        //idx isn't exist

        ptr = cur;
        //*ptr point to the string(visited this time)'s suffix's last char

        while (ptr != root && ptr->cnt != -1) {
            res += ptr->cnt;
            //the word exists cnt times

            ptr->cnt = -1; 
            //visited only once--flag*-1

            ptr = ptr->fail; 
            //along *fail

        } //calculate all the words' exsitence

        i++;
    }

    return res;
}

看一个具体的问题

Hdu 2222 http://acm.hdu.edu.cn/showproblem.php?pid=2222

题意 给定N个模式串 统计在一个长为M的主串里出现了多少个模式串

KMP算法可以做 复杂度为O(MN)

结合KMP算法和Trie树 AC自动机可以很好的解决这个问题

AC自动机的第一步是把所有模式串建成一个Trie

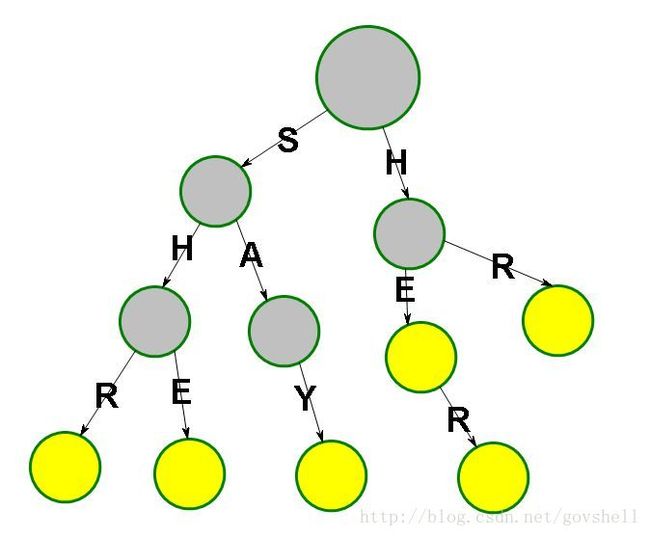
比如有模式串{SHE SHR SAY HE HR HER}

第一步.建立相应的Trie

主串为SHERSAY

和KMP算法的策略基本相同

AC自动机是从根节点开始根据主串的字母在Trie上走

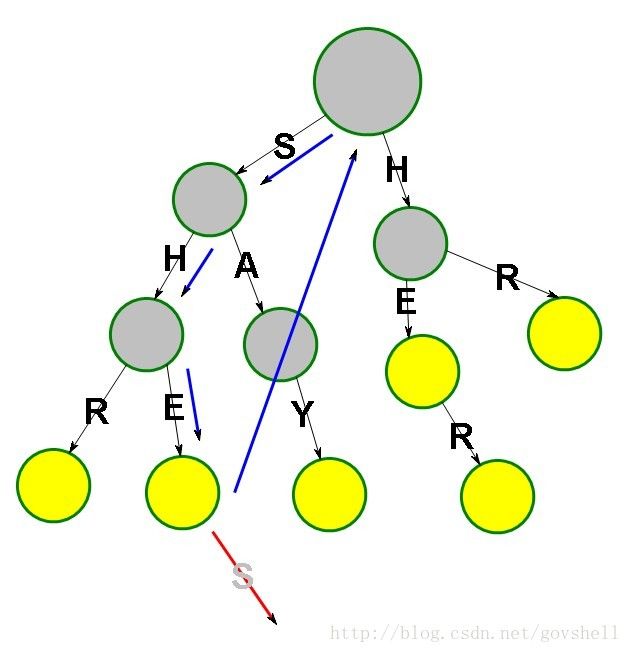
运气很好 我们只要在Trie上走三步就配到一个串SHE

正当我们想要继续的时候 发现下一个字母是S 在当前节点X上不能再向下了

只好再回头跳到根节点继续配

显然这样不断地 匹配就向下 不匹配就回溯到根 是可以得到正解的

但是最坏复杂度还是O(MN)

我们回想KMP算法 既然要回溯 不如回的少一点

我们在SHE配好之后 抬头一看 有个单词的前缀是HE 正好是SHE的后缀

我们就跳到HE的词尾节点 继续配这样就减少了运算量

假设还有E这个单词怎么办 我们显然是不往上回溯的 因为后缀E没有后缀HE长嘛

我们发现到了新的节点可以配出R这个字母 就继续向下 走了一步又发现无路可走了

抬头一看 什么也没发现 无奈之下回到根节点继续配 又欣喜的发现SAY可以配了

如此就匹配完了 由于走到了四个模式串的词尾

所以这个主串出现了 SHE HE HER SAY四个串

回顾我们的探索历程 我们借鉴了KMP的思路 利用了回溯来降低运算量

从SHE词尾到HE词尾 从HER词尾到Root 有两次回溯

这就是AC自动机的核心思想 Fail指针 顾名思义就是匹配失败了 回溯到哪里继续

这个和KMP的Next函数十分类似

回忆KMP的Next函数我们是通过线性递推来构造的

Trie是一棵树 我们就通过BFS来实现吧

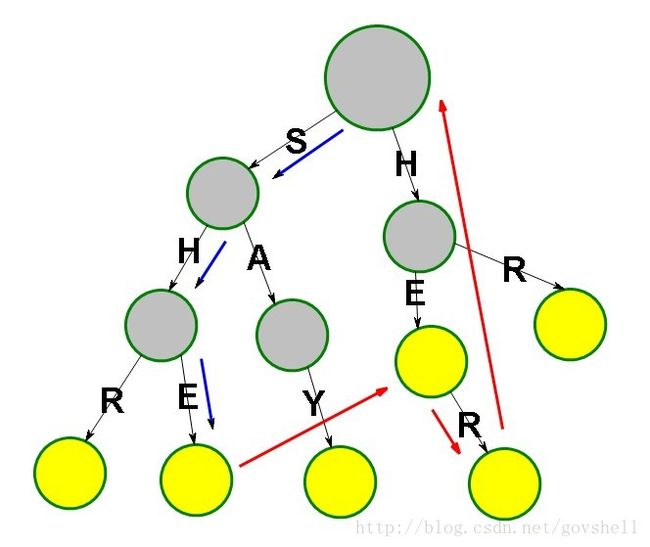
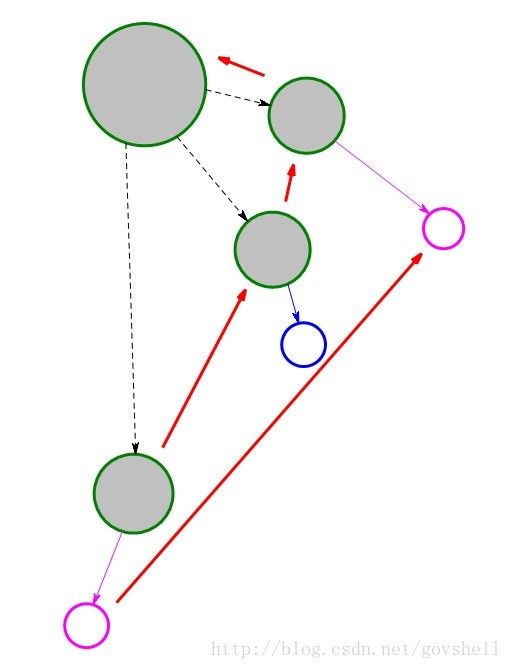
下图是构造好Fail指针的AC自动机

第二步.构建Fail指针
由于根节点的特殊性 我们不好把它的儿子和其他节点统一处理 于是就一个循环解决

然后开始BFS 我们把队首的儿子都依次处理好然后入队即可

寻找儿子的Fail指针 和KMP类似 从父亲开始不断的利用长辈的Fail指针回溯

直到一个长辈节点有一个儿子 和 父亲的这个儿子一样为止

把儿子的Fail指针连向长辈的儿子

如果走到根节点都没有这样的长辈 就把Fail指向Root

队空就结束了

注意到虚线代表的串 前面的串是后面串的后缀

理解这个BFS就不难了

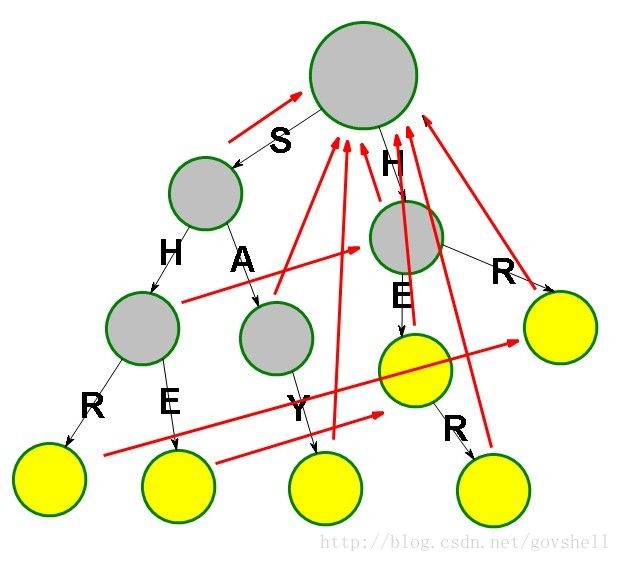
第三步.匹配

就是根据主串在自动机上走

匹配成功就向下走一步 不成功就沿着Fail指针回溯

复杂度达到了O(M)

很好理解 注意统计的细节即可