树状数组详解
树状数组
引入:
介绍一个东西总要先说它用来干嘛吧。树状数组简单点来说就是在一个数组的n过大时,我们去求这个数组的一段区间和时间复杂度太高,我们无法接受这么高的时间复杂度,因此用了树状数组这么一种结构来简化我们的区间求和复杂度。普通数组时间复杂度为O(n),树状数组为O(logn).
初步认识:
认识一个事物最直观的还是图啊。所以在这里我们给出一张图来辅助学习。我们在这里记原数组为A[],树状数组为C[]。
![]()
看吧,在这张图里面我们可以很直观地发现,倒数第一层地索引i全部为奇数,倒数第二层呢,全部是2的倍数而非4、8、16的倍数,第三层则是4的倍数而非8、16.。。的倍数。。一层一层递推上去。我们可以得到原数组和树状数组之间的关系。
C[1] = A[1];
C[2] = C[1]+C[2]=A[1]+A[2];
C[3] = A[3];
C[4] =C[2]+C[3]+A[4]= A[1]+A[2]+A[3]+A[4];
C[5] =A[5];
C[6] = C[5]+A[6]=A[5]+A[6];
C[7]=A[7];
C[8] = C[4]+C[6]+A[8]=A[1]+...A[8];
.....
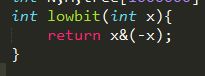
在这里我们先介绍一个lowbit()函数,来为下面用公式表示原数组和树状数组之间关系做铺垫。
这个函数是不详细介绍,我们只需要知道:当x是奇数时,lowbit返回值是1,当x是2*奇数时,返回值是2;当x是4*奇数时,返回值时4.。。。
依此递推。。
树状数组的建立
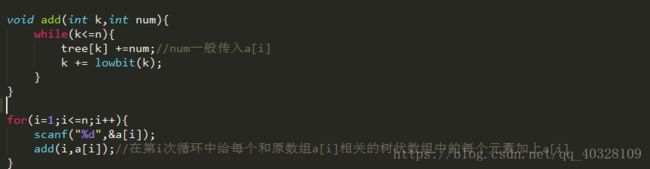
在了解了lowbit的基础上下面我们用一个实例来介绍怎么用原数组来建立树状数组吧。
假设这个n是8吧,现在博主亲手写下递推关系,更直观。
博主地字比较差,勿怪。。
总之,在i=1到n的循环中,
C[1]就加了一次a[1];
c[2]在i=1时加了一次a[1],在i=2时加了一次a[2],所以c[2]=A[1]+A[2];
c[3]在I=1和i=2时都未曾遍历到,所以它只有在i=3时才加上了一个A[3],所以C[3]=A[3];
C[4]在i=1、2、3、4时都遍历到了,所以C[4]=C[1]+C[2]+C[3]+C[4];
。。。剩下的自己推吧,都一个道理了的。
树状数组的应用
有初学者觉得,这个树状数组乱七八糟,乱八七糟的,step都没有一个特别明确的规律,我要他合用,请听博主细细道来,下面我们来介绍利用树状数组来求原数组的区间和。
emmm,这是一个有趣的函数:我们来列举一下x的不同情况吧。
当x=1时,i从1开始遍历,i-=lowbit(1),所以i直接等于0了,所以for循环直接结束,getsum=c[1]=A[1];
当x=2时,i从2开始遍历,i-=lowbit(2),所以i还是直接等于0了,for循环直接结束,getsum=c[2]=A[2];
我们把x变大一点吧,当x=7时,i从7开始遍历,sum+=c[7],7-=lowbit(7),此时i=6,sum+=c[6],6-=lowbit(6),此时i=4,sum+=c[4],4-=lowbit(4),然后i就变成0了,所以getsum=c[7]+c[6]+c[4]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]。
当x=8时,sum+=c[8],i-=lowbit(8),i就变成了0,小伙伴们还记得c[8]是多少吗,c[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
。
。
。
我们通过这一列举可以发现,将lowbit(x)作为遍历过程中的步长,我们使用getSum(x)可以得到原数组累加到A[x]的和,
那么此时我们如果要求原数组区间[l,r]的和(包括l和r),那我们就可以直接通过getsum(r)-getsum(l-1)来得到答案了。
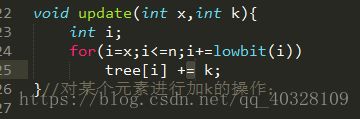
树状数组更新时的操作
有些初学者如果思考的深入的话,可能会提出这样一个问题,当我们改变了原数组中一个元素的值的时候,假如这个元素是A[x]吧,那这个树状数组岂不是很多元素都要改变值吗,因为树状数组表示的是原数组的和啊。那我们怎么改变在树状数组中和这个改变的元素相关的元素的值呢?不用着急,下面我们来给出答案:
通过这个函数,我们就可以实现树状数组值的更新啦。