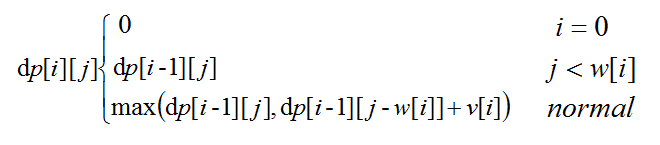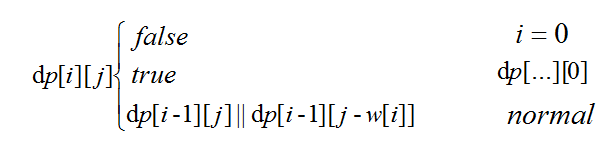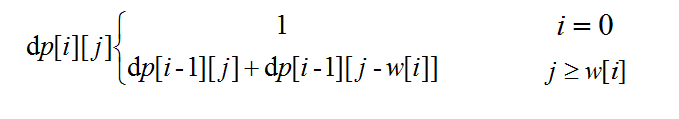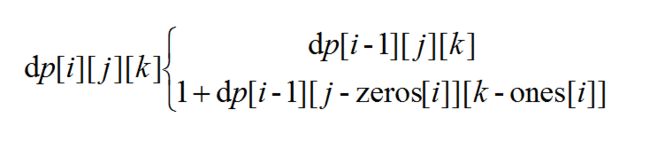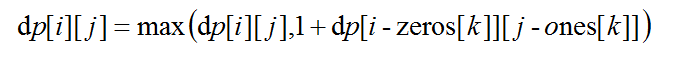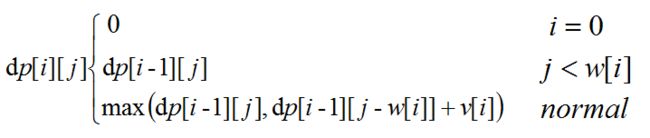Leetcode动态规划——01背包问题
内容参考
https://blog.csdn.net/yoer77/article/details/70943462
https://labuladong.github.io/ebook/动态规划系列/
https://leetcode-cn.com/problems/coin-change/solution/bei-bao-wen-ti-zhi-01bei-bao-wen-ti-ke-pu-wen-ji-c/
动态规划一般解决最值问题,题目只要问最值,但是不在乎得到最值的解法,基本可以考虑使用动态规划解决问题。
动态规划的部分问题可以归类为背包问题,下面介绍背包问题中最基础也是理解动态规划和所有背包问题的关键!
目录
01背包
【状态】
【状态方程】
【初始化(base case)】
【关于空间优化】
总结
416. 分割等和子集
494. 目标和
474. 一和零
1049. 最后一块石头的重量 II
01背包
有N个物品,该物品有两个属性,重量w[i],价值v[i]。
有背包一个,承重为W。
现在要求从这些物品中挑选出总重量不超过W的物品
求所有挑选方案中价值总和的最大值
每件物品都只有一件,要么进背包,要么不进,顾名思义为01背包
这个价值,可以是很多东西,可以是bool变量,可以是很多能够代指的内容。
【状态】
我们定义dp函数如下:
![]()
根据是否要求背包满载,分为两种情况,
- 在背包满载的情况下,所能取得的最大价值是多少
- 在背包可以不满载的情况下,所能取得的最大价值是多少
动态规划的核心,就是问题的分解,将复杂问题分解为有限个子问题(重叠子问题),求解子问题的最优解(最优子结构),
然后,将子问题和父问题联系起来(状态方程),过程中注意避免重复计算一些子问题(重叠子问题)。
那么我们给出了子问题的结构,也就是dp[i][j]。
如何将这个子问题和父问题联系起来呢?我们来看看dp[i][j]是怎么构成的:
解释:
- 如果拿了,那么第i-1的最优解加上第i个的价值(此时注意,剩余重量要改变),就是拿了第i个的最优解!
- 如果不拿,那么就是第i-1的最优解。此时的j可能需要根据题意来判断了,有时要求装满有时要求无所谓,但是这都不影响大局,只要不超出负重就行。
那么不可能以上两种情况兼得,取最优即可,取二者中的最值。
【状态方程】
如下:
目前为止,父问题和子问题都已经联系到一起了,也找到了最优子结构的部分。在代码部分注意重叠子问题,如果计算过的部分大可不必再算。
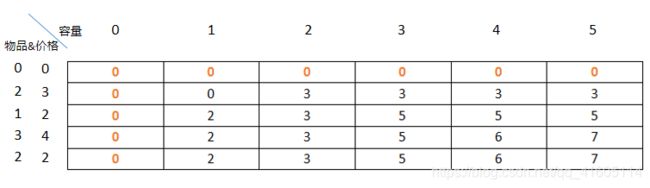
我们手动推导一下状态方程执行的过程,看看问题所在
其实整个动态规划就是在填这个变,i的起点是1,终点是2,j的起点是1,终点是5,i和j均为零的情况没有意义,单纯的在初始化中全部初始化为0即可。
程序也是这么指向的,从上面表格黑色部分的左上角开始,按照行遍历
(但是要注意,题目一旦对达到最优解时背包一定要满载,那么初始化情况会有所变化)
表中的内容就是在第1~i个物品中挑选,在不超出规定的重量下,计算得出的最大价值。
表中红色内容,都是需要我们初始化(base case)的,而且也都是容量太小,一个物品也放不进去的情况。
从表中也可以看出,我们dp初始化的大小一定要是(n+1)x(w+1),因为第i个元素,在数组中的下标是i-1。
我们要求dp【n】【w】,大小自然是(n+1)x(w+1)
模板(记忆化递归):
#include
#include
#define MAXN 1000
using namespace std;
int w[MAXN] = {0, 2, 1, 3, 2};
int v[MAXN] = {0, 3, 2, 4, 2};
int dp[MAXN][MAXN]; //记录搜索过的结果
int W = 5, n = 4;
//自上而下
int Rec(int i, int j) {
//Rec(i, j)计算过,直接拿来用
if (dp[i][j] != -1) return dp[i][j];
int res;
if (i == 0) {
res = 0;
}
else if (j < w[i]) {
res = Rec(i-1, j);
}
else {
res = max(Rec(i-1, j), Rec(i-1, j-w[i]) + v[i]);
}
return dp[i][j] = res; //记录
}
int main() {
memset(dp, -1, sizeof(dp));
cout << Rec(n, W) << endl;
return 0;
}
//自下而上
int back(int W, int N, vector& wt, vector& val) {
// base case 务必注意
vector> dp(N + 1, vector(W + 1, 0));
for (int i = 1; i <= N; i++)
{
for (int w = 1; w <= W; w++)
{
if (w < wt[i-1])
{
dp[i][w] = dp[i - 1][w];
} else {
dp[i][w] = max(dp[i - 1][w],dp[i - 1][w - wt[i-1]] + val[i-1]);
}
}
}
return dp[N][W];
}
(来源:https://blog.csdn.net/yoer77/article/details/70943462)
我们看一下整个过程中的递归情况,更好的方便理解,此模板是典型的递归,至上而下的动态规划:
Rec(4, 5)
/ \
Rec(3, 3) Rec(3, 5)
/ \ / \
Rec(2, 0) Rec(2, 3) Rec(2, 2) Rec(2, 5)
/ / \ / \ / \
Rec(1, 0) Rec(1, 2) Rec(1, 3) Rec(1, 1) Rec(1, 2) Rec(1, 4) Rec(1, 5)
/ / \ / \ / / \ / \ / \
(0,0) (0,0) (0,2) (0,1) (0,3) (0,1) (0,0) (0,2) (0,2) (0,4) (0,3) (0,5)
(来源:https://blog.csdn.net/yoer77/article/details/70943462)
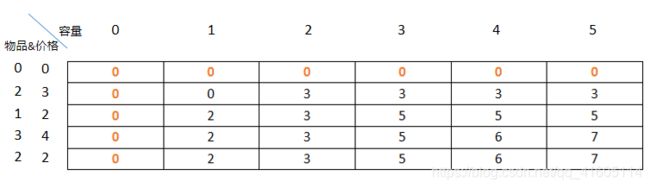
【初始化(base case)】
![]()
以上内容是方法论,理解起来可能有些抽象,那么看几道实例,有助于理解
【关于空间优化】
参考:https://www.cnblogs.com/yxym2016/p/12684203.html
普通模式:
对应程序:
int knapback(int W, int N, vector& wt, vector& val) {
// base case 务必注意
vector> dp(N + 1, vector(W + 1, 0));
for (int i = 1; i <= N; i++)
{
for (int w = 1; w <= W; w++)
{
if (w < wt[i-1])
{
dp[i][w] = dp[i - 1][w];
} else {
dp[i][w] = max(dp[i - 1][w],dp[i - 1][w - wt[i-1]] + val[i-1]);
}
}
}
return dp[N][W];
}
i等于2时,dp的更新,都和i等于1时的数据有关。从上面的程序很容易看到这点。 也就是程序在填第三行的表的时候,需要第二行的数据,那么第一行,是不是就多余了?完全不需要了。所谓的数据优化,就是优化掉不需要的“第一行”。那么这只是个特例,放在程序中,普通模式,是将二维数组的内容全部列出来,那么优化方法,就是最新值覆盖旧数据。
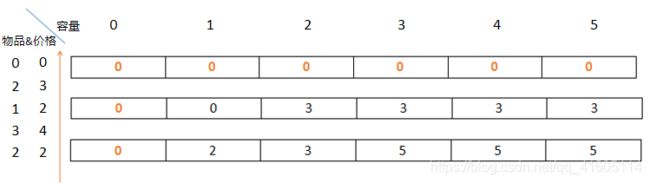
下面我们还是以表格的形式,来看看整个过程
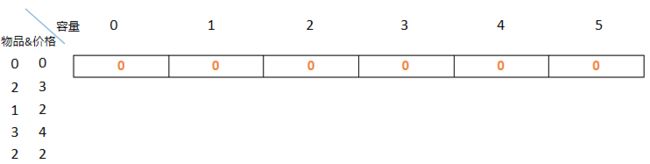
将二维数组改为一维数组,并和二维数组一样,初始化为0
我们的i还是从1开始,也就是物品重量2价值3开始,填表,并覆盖旧值
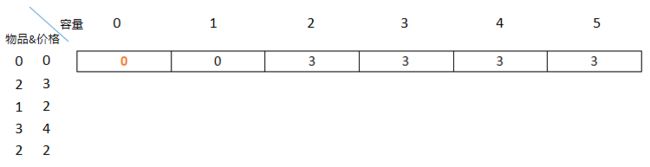
容量1,放不进去物品,价值为0;容量大于等于2,可以放入,价值均为3,如下图:
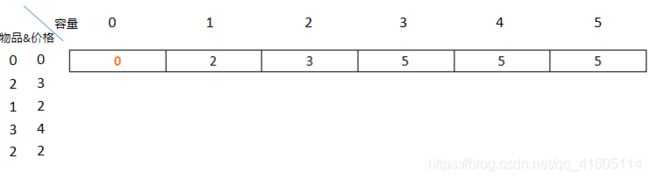
我们继续,i此时等于2,容量大于等于3,最高价值均为5,如下图:
此时我们也看出了规律,也看出来所谓的空间优化的奥秘:
沿着红色箭头,不断覆盖即可。下面我们看看程序怎么写
int knapback(int W, int N, vector& wt, vector& val) {
// base case 务必注意
vector> dp(N + 1, vector(W + 1, 0));
for (int i = 1; i <= N; i++)
{
for (int w = W; w >=wt[i-1]; w--)
{
if (w >= wt[i-1])
dp[w] = max(dp[w],dp[w - wt[i-1]] + val[i-1]);
}
}
return dp[N][W];
} 01背包是逆序,因为必须保证dp[i][j]的状态是由dp[i-1]推导而来的。
也是为了能保证每个物品只选择一次,保证在考虑入选第i件物品时,依据的是绝对没有选入i的dp[i-1]推导而来的。
外循环没有变化,内循环是逆序遍历,从表达式中我们也能看出正序遍历没有办法完成。
总结
不仅仅是背包问题,动态规划的所有问题,都是按照下面的思维模式进行解决的。
题目只要问最值,但是不在乎得到最值的解法,基本可以考虑使用动态规划解决问题
【状态】:问题求什么,要什么,我们dp的因变量就是什么,自变量根据题目要求,为物品和容量
【状态方程】确定好了状态,就要看看这个父问题如何转换为子问题了,这也是状态方程要解决的
【初始化】主要是看有没有要求得到最值的时候,满负载
【考虑压缩空间】自变量如果能从物品和容量单纯的变成容量,那自然是好事
以上都是方法论,我们看看Leetcode中典型的01背包问题,看看如何入手解决:
416. 分割等和子集
https://leetcode-cn.com/problems/partition-equal-subset-sum/
问题被转化为,给定背包容量为(sum/2),选择物品放入,恰好等于背包容量(正好把背包放满),能做到为true,反之为false
问题转化为:
有背包一个,承重为sum/2。
现在要求从这些物品中挑选出总重量不超过sum/2的物品
求所有挑选方案中是否能把背包放满
在1~i个数字中任意选择,能够组成和为j,则为true,反之为false。
我们再理解一下状态方程
class Solution {
public:
bool canPartition(vector& nums) {
//不使用模板
// if(nums.empty()) return false;
int size = nums.size();
int sum = 0;
for(auto item:nums) sum+=item;
if(sum%2!=0) return false;
sum =sum/2;
vector>dp(size+1,vector(sum+1,false));
//从前i个里面挑,能组成sum的可能性
//base case
dp[0][0] = true;
for(int i = 1;i<=size;++i)//前i个数字
{
for(int j = 1;j<=sum;++j)
{
if(j-nums[i-1]>=0)
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
else
dp[i][j] = dp[i-1][j];
}
}
return dp[size][sum];
}
};
从模板到例题,背包问题的核心,其实就是对dp的理解
![]()
那么我们优化一下代码:
class Solution {
public:
bool canPartition(vector& nums) {
//背包满载sum/2,n个物品,刚好放满
int size = nums.size();
if(size == 0) return false;
int sum = 0;
for(auto numval:nums) sum += numval;
if(sum%2 != 0) return false;//无法平分,那么肯定是无法分割的
sum = sum/2;
vector dp(sum + 1, false);//初始化
for (int i = 0; i <= size; i++)
dp[0] = true;//背包负载为零的情况,也就是装满了,那肯定是true
for(int i = 1;i<=size;++i)
{
for(int j = sum;j>=nums[i-1];--j)
{
if(j>=nums[i-1])//数组的索引是从0开始,i是从1开始
dp[j] = dp[j]||dp[j-nums[i-1]];
}
}
return dp[sum];
}
};
494. 目标和
https://leetcode-cn.com/problems/target-sum/
(解法)https://leetcode-cn.com/problems/target-sum/solution/c-dfshe-01bei-bao-by-bao-bao-ke-guai-liao/
class Solution {
public:
int findTargetSumWays(vector& nums, int S) {
return dfs(nums,0 ,S, 0);
}
int dfs(vector &nums,int temp,uint target, int left) {
if (temp == target && left == nums.size()) return 1;
if (left >= nums.size()) return 0;
int ans = 0;
ans += dfs(nums,temp-nums[left],target,left + 1);
ans += dfs(nums,temp+nums[left],target,left + 1);
return ans;
}
}; 暴力解法,从零开始,对数组中的数值有加有减,整个过程可以变成一个二叉树,那么我们遍历二叉树,在叶子结点处,找到数值为target目标值的叶子结点即可完成。
(参考结题思路:)
https://leetcode-cn.com/problems/target-sum/solution/mu-biao-he-by-leetcode/
https://leetcode-cn.com/problems/target-sum/solution/python-dfs-xiang-jie-by-jimmy00745/
使用01背包问题模板解决的话,需要推导一个公式:
来源:https://leetcode-cn.com/problems/target-sum/solution/c-dfshe-01bei-bao-by-bao-bao-ke-guai-liao/
问题转化为:
有背包一个,承重为(S+sum)/2。
现在要求从这些物品中挑选出总重量恰好等于(S+sum)/2的方案,有多少种
此题中要求每次必须满载,那么初始化其余情况都是0,当承重为0时,自然是一种方案,dp【0】=1;
而状态方程也很好写。
此时二者应该相加,才是可行的所有方案
下面程序是优化版本:
class Solution {
public:
int findTargetSumWays(vector& nums, int S) {
int size = nums.size();
if(size ==0) return 0;
long sum = 0;//防止内容很大
for(auto item:nums) sum += item;
if((S+sum)%2 != 0||S > sum) return 0;//防止内容很大
sum = (S+sum)/2;//找一个
vectordp(sum+1,0);
dp[0] = 1;
for(int i = 1;i<=size;++i)
{
for(int j = sum;j>=nums[i-1];--j)
{
dp[j] = dp[j] + dp[j-nums[i-1]];
}
}
return dp[sum];
}
}; 474. 一和零
https://leetcode-cn.com/problems/ones-and-zeroes/
思考方式1:(不优化)
此题是典型的动态规划问题,只求最值,不在乎最值的解。
凭借我们的经验,选择字符串这个部分,也就是i的部分,完全可以忽略,做个优化,下面是优化版本
思考方式2:(优化)
题目要什么我们就设置什么为我们的【状态】
之前都是一个背包,现在是两个,一个是0,一个是1,按照原版本背包问题,此题的状态应该是:
【状态方程】
zeros和ones分别表示,k中包含0和1的个数。
问题转化为:
有背包一个,承重为i+j。
现在要求从这些物品中挑选出总重量不超过i+j的物品
求所有挑选方案中最多能挑选几个物品
不优化程序和思路的解法:
https://leetcode-cn.com/problems/ones-and-zeroes/solution/dong-tai-gui-hua-zhuan-huan-wei-0-1-bei-bao-wen-ti/
leetcode中关于整个过程进行了非常详细的赘述。
https://leetcode-cn.com/problems/ones-and-zeroes/solution/yi-he-ling-by-leetcode/
class Solution {
public:
int findMaxForm(vector& strs, int m, int n) {
vector> dp(m+1,vector(n+1,0));
//因为没有要求全部用完0和1,所以初始状态可以设置为0,如果要求全部使用完,那么除了dp[0][0] = 0,其他都是无效状态
int zeros = 0,ones = 0;
for(auto item : strs)
{
zeros = numbers(item,'0');
ones = numbers(item,'1');
for(int i = m;i>=zeros;--i)
{
for(int j = n;j>=ones;--j)
{
dp[i][j] = max(dp[i][j],1+dp[i-zeros][j-ones]);
}
}
}
return dp[m][n];
}
int numbers(string& strs,char cval)
{
int Numbers = 0;
for(auto item : strs)
{
if(item == cval) ++Numbers;
}
return Numbers;
}
}; 三个循环嵌套,第一个外循环是选择字符串,第二个外循环是选择0的个数,第三个循环是1的个数,也就是在选择了一个字符串的情况下,在不同的m和n的组合下,所能产生的所有组合情况。
1049. 最后一块石头的重量 II
https://leetcode-cn.com/problems/last-stone-weight-ii/
将题目所给的数组分成两个部分:两个部分的和,约接近越好。
那么有如下状态:
问题转化为,
有背包一个,承重为j。
现在要求从这些物品中挑选出总重量不超过j的物品
求所有挑选方案中物品总重量最接近j的重量是多少
那么程序如下:
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int size = stones.size();
int sum = 0;
for(auto item : stones) sum += item;
int target = sum/2;
vector> dp(size+1,vector(target+1,0));
for(int i = 1;i<=size;++i)
{
for(int j = 1;j<=target;++j)
{
if(j 对以上内容进一步优化:
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int size = stones.size();
int sum = 0;
for(auto item : stones) sum += item;
int target = sum/2;
vector dp(target+1,0);
for(int i = 1;i<=size;++i)
{
for(int j = target;j>=stones[i-1];--j)
{
dp[j] = max(dp[j],dp[j-stones[i-1]]+stones[i-1]);//务必i-1
}
}
return sum - 2*dp[target];
}
}; 其他部分:
class Solution {
public:
int lastStoneWeightII(vector& stones) {
if(stones.empty()) return 0;
int size = stones.size();
int sum = 0;
for(auto item:stones) sum += item;
int half = sum/2;
vector>dp(size+1,vector(half+1,0));
//从前i个石头里面拿,上限是half,拿到的石头最终
for(int i = 1;i<=size;++i)
{
for(int j = 1;j<=half;++j)
{
if(j-stones[i-1]>=0)
dp[i][j] = max(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
else dp[i][j] = dp[i-1][j];
}
}
return sum - 2*dp[size][half];
//dp[size][half]可以和总和中总和相同的石头抵消重量
//所以sum - 2*dp[size][half],相当于减去完全抵消的部分,最后就是剩余的
}
};