数据结构-二叉树基础题目小结（遍历，求节点数目等等）

给定一个前序序列数组构造一个二叉树

思路：首先序列中要有给定的非法值，也就是二叉树中对应的空节点；对于构造一个二叉树可以使用递归的思想：先构造当前节点，再构造左子树，再右子树，直到遇到非法值时，将NULL返回，使得上一个节点的一端链接到NULL，图示如下：

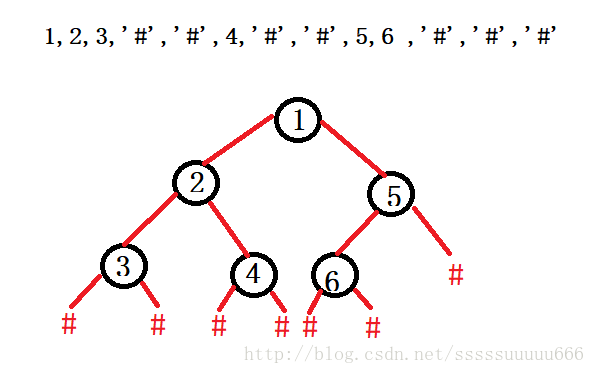
    /*  int arr[] = { 1,2,3,'#','#',4,'#','#',5,6 ,'#','#','#' };
    BinaryTree<int> tree1(arr, sizeof(arr) / sizeof(arr[0]), '#');*/

    BinaryTree(const T* arr, size_t sz, const T& invalid)
    {
        size_t index = 0;
        _root = _CreatTree(arr, sz, index, invalid);
    }

    Node* _CreatTree(const T* arr, size_t sz, size_t& index, const T& invalid)
    {
        Node* node = NULL;
        if (arr[index] != invalid)
        {
            node = new Node(arr[index]);
            node->_left = _CreatTree(arr, sz, ++index, invalid);
            node->_right = _CreatTree(arr, sz, ++index, invalid);
        }
        return node;
    }

---

前、中、后序遍历递归写法：

前序遍历：先遍历根节点，再遍历左子树，再遍历右子树；所以最先输出根节点；

中序遍历：先遍历根节点左子树，再遍历根节点，再遍历右子树；

后序遍历：先遍历左子树，再右子树，最后根节点。

//前序
    void PrevOrederR()
    {
        _PrevOrederR(_root);
        cout<<endl;
    }

    void _PrevOrderR(Node* node)
    {
        if (node == NULL)
            return;

        cout << node->_data << " ";
        _PrevOrderR(node->_left);
        _PrevOrderR(node->_right);
    }

//中序
    void MidOrderR()
    {
        _MidOrderR(_root);
        cout<<endl;
    }

    void _MidOrderR(Node* node)
    {
        if (node == NULL)
            return;

        _MidOrder(node->_left);
        cout << node->_data << " ";
        _MidOrder(node->_right);
    }

//后序
    void BackOrderR()
    {
        _BackOrderR(_root);
        cout<<endl;
    }


    void _BackOrderR(Node* node)
    {
        if (node == NULL)
            return;

        _BackOrderR(node->_left);
        _BackOrderR(node->_right);
        cout << node->_data << " ";
    }

输出结果：拿一开始构造的二叉树为例

---

前、中、后序遍历非递归写法：

思路：将递归转递归无非就是转为循环或者使用栈来模拟递归的过程；前序和后序比较简单，在后序遍历时需要注意加判断当前节点的右子树是否已经遍历过，只有当左右子树都遍历过后，才可输出当前根节点。

    //遍历非递归
    void PrevOrderNR()
    {
        stack s;
        Node* cur = _root;
        while (cur || !s.empty())
        {
            while (cur != NULL)
            {
                s.push(cur);
                cout << cur->_data << " ";
                cur = cur->_left;
            }
            //到最左根节点，该回溯了
            if (!s.empty())
            {
                cur = s.top();
                s.pop();
                cur = cur->_right;
            }
        }
        cout << endl;
    }

    void MidOrderNR()
    {
        stack s;
        Node* cur = _root;

        while (cur != NULL || !s.empty())
        {
            while (cur != NULL)
            {
                s.push(cur);
                cur = cur->_left;
            }

            //到最左节点
            if (!s.empty())
            {
                cur = s.top();
                cout << cur->_data << " ";
                s.pop();
                cur = cur->_right;
            }
        }
        cout << endl;
    }

    void BackOrderNR()
    {
        stack s;
        Node* cur = _root;
        Node* prev = NULL;

        while (cur != NULL || !s.empty())
        {
            while (cur != NULL)
            {
                s.push(cur);
                cur = cur->_left;
            }

            Node* top = s.top();

            if (top->_right == NULL || top->_right == prev)
            {
                cout << top->_data << " ";
                s.pop();
            }
            else
            {   //说明此时右子树还没判断，不可直接pop
                cur = top->_right;
            }
            prev = top;
        }
        cout << endl;
    }

输出结果：

---

层序遍历：

思路：利用队列先进先出的特性完成

    void LevelOrder()
    {
        queue q;
        Node* node = _root;
        if (node != NULL)
            q.push(node);

        while (!q.empty())
        {
            Node* cur = q.front();
            cout << cur->_data << " ";
            q.pop();
            if (cur->_left != NULL)
                q.push(cur -> _left);
            if (cur->_right != NULL)
                q.push(cur->_right);
        }
        cout << endl;
    }

//输出结果：1 2 5 3 4 6

---

求节点数目：

思路一：利用子问题的思想：左子树节点个数加右子树节点个数加自己的一个，如果当前节点为NULL，则返回0；

    int SizeByChildQue()
    {
        return _SizeByChildQue(_root);
    }

    int _SizeByChildQue(Node* node)
    {
        if (node == NULL)
            return 0;
        return _SizeByChildQue(node->_left) + _SizeByChildQue(node->_right) + 1;
    }

---

思路二：利用遍历的思想：给定一个参数，遍历所有节点，只要不为NULL，节点个数加1

    int SizeByTrav()
    {
        size_t size = 0;
        _SizeByTrav(_root, size);
        return size;
    }

    void _SizeByTrav(Node* node, size_t& size)
    {
        if (node == NULL)
            return;

        size++;
        _SizeByTrav(node->_left, size);
        _SizeByTrav(node->_right,size);
    }

---

求叶子节点数目：如同求节点数目，只不过在统计数目时需要判断是否左右都为NULL，所以也可分为两种写法：

思路一：子问题：左子树叶子节点个数加右子树叶子节点个数，同时还要注意如果只有一个节点。

    int LeafSizeByChildQue()
    {
        return _LeafSizeByChildQue(_root);
    }

    int _LeafSizeByChildQue(Node* node)
    {
        if (node == NULL)
            return 0;

        //进行判断，只有当左右都为空时才算做一个叶子节点
        if (node->_left == NULL && node->_right == NULL)
        {
            return 1;
        }
        return _LeafSizeByChildQue(node->_left) + _LeafSizeByChildQue(node->_right);
    }

---

思路二：遍历思想，只有当当前节点为叶子节点时，才对计数+1；切记size要传引用，否则回到第一个栈帧时size仍为0！

    int LeafSizeByTrav()
    {
        size_t size = 0;
        _LeafSizeByTrav(_root, size);
        return size;
    }

    void _LeafSizeByTrav(Node* node, size_t& size)
    {
        if (node == NULL)
            return;

        if (node->_left == NULL && node->_right == NULL)
            size++;

        _LeafSizeByTrav(node->_left, size);
        _LeafSizeByTrav(node->_right, size);
    }

---

二叉树的高度：

思路：需要注意的是，高度是最长的那条路；划分为子问题为：该节点的高度等于左子树和右子树高度中大的那个再加上1。

    size_t Height()
    {
        return _Height(_root);
    }

    size_t _Height(Node* node)
    {
        if (node == NULL)
            return 0;

        size_t lHeight = _Height(node->_left);
        size_t rHeight = _Height(node->_right);
        //注意返回时要加上当前的高度1
        return lHeight > rHeight ? lHeight + 1 : rHeight + 1;
    }

---

完整代码可查看https://github.com/SssUuuu/Data_structure/blob/master/BinaryTree.h