R语言实现主成分分析与典型相关分析

《数据分析方法》–梅长林 各章原理及R语言实现

1. 数据描述性分析
2. 回归分析
3. 方差分析
   4. 主成分分析与典型相关分析
4. 判别分析
5. 聚类分析
6. Bayes统计分析

4.1主成分分析

4.1.1总体主成分的求法

  求主成分归结为求样本（$X$）的协方差矩阵$\Sigma$的特征值和特征向量问题，具体由如下结论：

  设$\Sigma$是$X=(X_1,X_2,...,X_p{)}^T$的而协方差矩阵，其特征值按大小顺序排列为${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_p\ge 0$，相应的正交单位化向量为 $e_1,e_2,...,e_p$，则$X$的第$k$个主成分可表示为

$$Y_k=e_k^{T}X=e_{k1}{X}_1+e_{k2}{X}_2+...+e_{kp}{X}_p,k=1,2,...,p,$$

  其中$e_k=(e_{k1},e_{k2},...,e_{kp}{)}^T$,并且我们知道$e_{k1}{X}_1,e_{k2}{X}_2,...,e_{kp}{X}_p$相互独立，这时有：

$$\{\begin{array}{ll}& Var(Y_k)=e_k^T\Sigma e_k={\lambda }_k{e}_k^T{e}_k={\lambda }_k,k=1,2,...,p,\\ & Cov(Y_j,Y_k)=e_j^T\Sigma e_k={\lambda }_k{e}_j^T{e}_k=0,j\ne k,\end{array}$$

  事实上，令$P=(e_1,e_2,...,e_p)$，则$P$为正交矩阵，且

$$P^T\Sigma P=\Lambda =Diag({\lambda }_1,{\lambda }_2,...,{\lambda }_p)，$$

  其中$Diag({\lambda }_1,{\lambda }_2,...,{\lambda }_p)$表示对角矩阵（因为协方差矩阵是实对称矩阵，所以可以正交对角化）。

  若$Y_1=a_1^{T}X$为$X$的第一主成分，其中$a_1^T{a}_1=1$（约束条件：a的模为1，要不方差可以无穷大）令

$$z_1=(z_{11},z_{12},...,z_{1p}{)}^T=P^T{a}_1$$

  则$z_1^T{z}_1=a_1^{T}P{P}^T{a}_1=a_1^T{a}_1=1,且$

$$\begin{array}{rl}Var(Y_1)& =a_1^T\Sigma a_1=z_1^T{P}^T\Sigma P{z}_1\\ & ={\lambda }_1{z}_{11}^2+{\lambda }_2{z}_{12}^2+...+{\lambda }_p{z}_{1p}^2\\ & \le {\lambda }_1{z}_1^T{z}_1={\lambda }_1\end{array}$$

  并且当$z_1=(1,0,..,0{)}^T$时，等号成立，这时

$$a_1=P{z}_1=e_1，$$

  由此可知，在约束条件$a_1^T{a}_1=1$之下，当$a_1=e_1$时，$Var(Y_1)$达到最大，且

$$\underset{a_1^T\Sigma a_1}{\max }\{Var(Y_1)\}=Var(e_1^{T}X)=e_1^T\Sigma e_1={\lambda }_1$$

  设$Y_2=a_2^T$为$X$的第二主成分，则应有

$$a_2^T{a}_2=1且Cov(Y_2,Y_1)=a_2^T\Sigma e_1={\lambda }_1{a}_2^T{e}_1=0,（Y_2、Y_1相互独立）$$
  即$a_2^T{e}_1=0.$令
$$z_2=(z_{21},z_{22},...,z_{2p}{)}^T=P^T{a}_2$$

  则$z_2^T{z}_2=1$，而由$a_2^T{e}_1=0$即有

$$a_2^T{e}_1=z_2^T{P}^T{e}_1=z_{21}{e}_1^T{e}_1+z_{22}{e}_2^T{e}_1+...+z_{2p}{e}_p^T{e}_1=z_{21}=0$$

  故

$$\begin{array}{rl}Var(Y_2)& =a_2^T\Sigma a_2=z_2^T{P}^T\Sigma P{z}_2=z_2^T\Lambda z_2\\ & ={\lambda }_1{z}_{21}^2+{\lambda }_2{z}_{22}^2+...+{\lambda }_p{z}_{1p}^2\\ & ={\lambda }_2{z}_{22}^2+...+{\lambda }_p{z}_{1p}^2\le {\lambda }_2{z}_2^T{z}_2={\lambda }_2\end{array}$$

  当$z_2=(0,1,0,...,0{)}^T$时，即$a_2=P{z}_2=e_2$时，满足$a_2^T{a}_2=1$,且$Cov(Y_2,Y_1)={\lambda }_1{a}_2^T{e}_1=0$，并且使$Var(Y_2)={\lambda }_2$达到最大

4.1.2总体主成分的性质

（1）主成分的协方差矩阵及总方差

（2）主成分的贡献率与累计贡献率

（3）主成分$Y_I$与$X_j$的相关系数 $Cov(X)=\Sigma =({\sigma }_{ij}{)}_{p\times p}$

4.1.3 R语言根据原理自己实现

求协方差矩阵

$$\left[\begin{array}{ccc}1& -2& 0\\ -2& 5& 0\\ 0& 0& 2\end{array}\right]$$
的各主成分

## 生成协方差矩阵
df = matrix(c(1, -2, 0, -2, 5, 0, 0, 0, 2), ncol=3)
df

A matrix: 3 × 3 of type dbl

1	-2	0
-2	5	0
0	0	2

利用R语言的内置函数eigen求特征值特征向量
用法：
eigen(x, symmetric, only.values = FALSE, EISPACK = FALSE)

参数	说明
x	a numeric or complex matrix whose spectral decomposition is to be computed. Logical matrices are coerced to numeric.
symmetric	if TRUE, the matrix is assumed to be symmetric (or Hermitian if complex) and only its lower triangle (diagonal included) is used. If symmetric is not specified, isSymmetric(x) is used.
only.values	if TRUE, only the eigenvalues are computed and returned, otherwise both eigenvalues and eigenvectors are returned.
EISPACK	logical. Defunct and ignored.

结果有两个：

1. values：特征值
2. vectors：特征向量

## 特征向量
eigen(df)$vectors

A matrix: 3 × 3 of type dbl

-0.3826834	0	0.9238795
0.9238795	0	0.3826834
0.0000000	1	0.0000000

## 特征值
eigen(df)$values

1. 5.82842712474619
2. 2
3. 0.17157287525381

所以X的三个主成分为：

$$\begin{array}{rl}{Y}_1& =e_1^{T}X=-0.383X_1+0.924X_2;\\ Y_2& =e_2^{T}X=X_3;\\ Y_3& =e_3^{T}X=0.924X1+0.383X_2;\end{array}$$

由上述结果可知，第一主成分的贡献率为：

$$\frac{5.83}{5.83+2.00+0.17}=73$$

前两主成分的累计贡献率为：
$$\frac{5.83+2.00}{5.83+2.00+0.17}=989$$

因此，若用前两个主成分代替原来的三个变量，其信息损失仅为2%，是很小的。

4.1.4 R语言内置方法

R中作为主成分分析最主要的函数是 princomp() 函数

1. princomp() 主成分分析 可以从相关阵或者从协方差阵做主成分分析
2. summary() 提取主成分信息
3. loadings() 显示主成分分析或因子分析中载荷的内容
4. predict() 预测主成分的值
5. screeplot() 画出主成分的碎石图
6. biplot() 画出数据关于主成分的散点图和原坐标在主成分下的方向

1.princomp()

## princomp()
df = data.frame(x1=rnorm(100), x2=rnorm(100), x3=rnorm(100))
df.pr=princomp(df,cor=FALSE) # cor=TRUE：以X的相关系数矩阵做主成分分析，其实就是X的标准化变量的主成分
df.pr

Call:
princomp(x = df, cor = FALSE)

Standard deviations:
   Comp.1    Comp.2    Comp.3 
1.0784416 0.9679190 0.8492227 

 3  variables and  100 observations.

其中Standard deviations代表各主成分的标准差，即根号特征值（特征值是主成分的方差）

2.summary()

summary(df.pr,loadings=TRUE) 

Importance of components:
                         Comp.1    Comp.2    Comp.3
Standard deviation     1.078442 0.9679190 0.8492227
Proportion of Variance 0.412266 0.3320949 0.2556392
Cumulative Proportion  0.412266 0.7443608 1.0000000

Loadings:
   Comp.1 Comp.2 Comp.3
x1         0.998       
x2 -0.120        -0.991
x3  0.992        -0.121

其中Proportion of Variance是各主成分的贡献率

Cumulative Proportion是累计贡献率

Loadings是特征向量

3.predict()

predict(df.pr, data.frame(x1=c(1, 2), x2=c(3, 4), x3=c(4, 5))) # 预测自给的数据
#predirc(df.pr) # 预测已有数据的主成分

A matrix: 2 × 3 of type dbl

Comp.1	Comp.2	Comp.3
3.770027	0.9634912	-3.532819
4.671794	1.9991897	-4.588350

4.loadings()

loadings(df.pr)

Loadings:
   Comp.1 Comp.2 Comp.3
x1         0.998       
x2 -0.120        -0.991
x3  0.992        -0.121

               Comp.1 Comp.2 Comp.3
SS loadings     1.000  1.000  1.000
Proportion Var  0.333  0.333  0.333
Cumulative Var  0.333  0.667  1.000

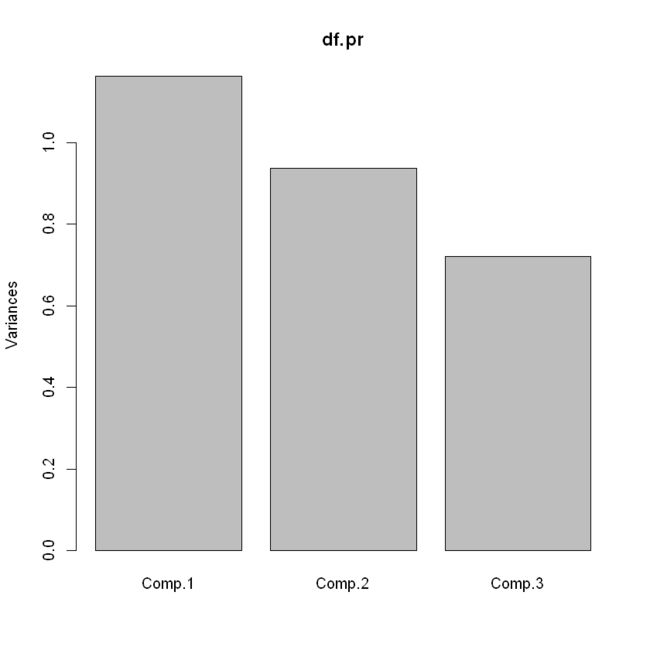
5.screeplot()

## 条形碎石图
screeplot(df.pr)

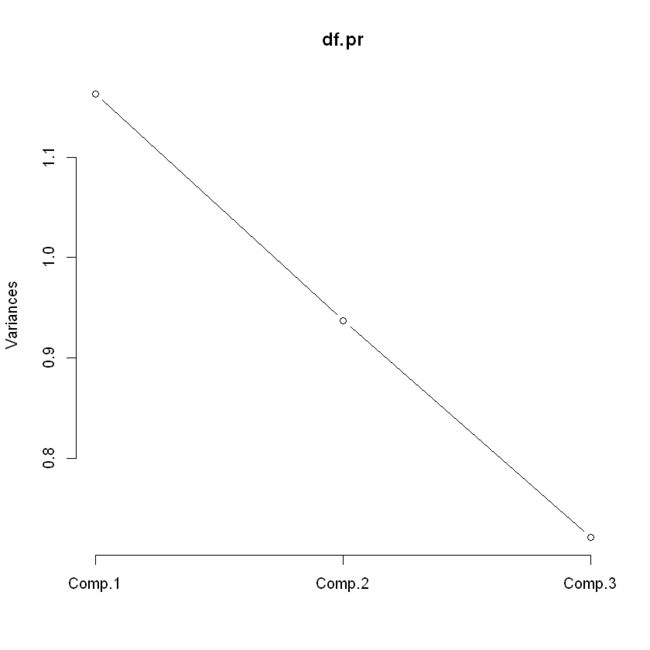
## 折现碎石图
screeplot(df.pr, type='lines')

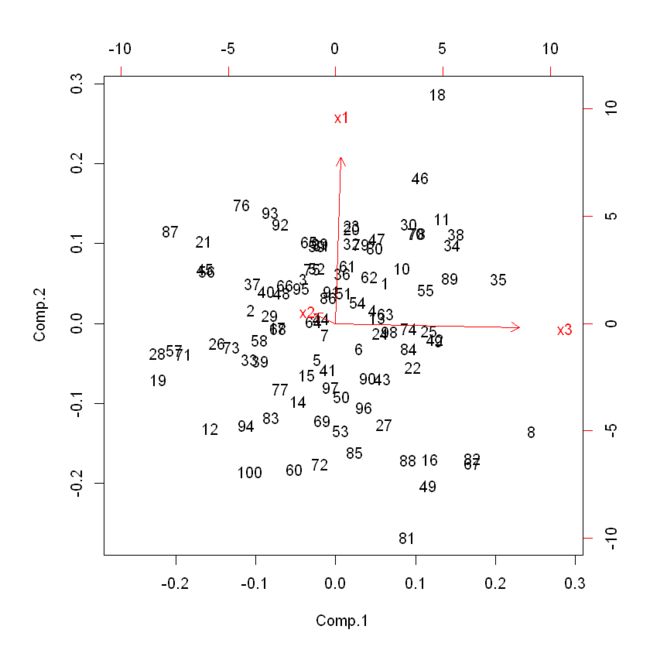
6.biplot()

## 主成分散点图
biplot(df.pr)

4.2 典型相关分析

## 相关系数矩阵
CorX `= matrix(c(1, 0.571, 0.875, 0.571, 1, 0.781, 0.875, 0.781, 1), ncol=3)
CorY = matrix(c(1, 0.671, 0.785, 0.671, 1, 0.932, 0.785, 0.932, 1), ncol=3)
CorXY = matrix(c(0.714, 0.840, 0.914, 0.380, 0.681, 0.591, 0.626, 0.819, 0.870), ncol=3)
CorYX = t(CorXY)

# 求负二次幂
fuermi<-function(Sigma){
  lamda <- solve(eigen(Sigma)$vectors)%*%Sigma%*%(eigen(Sigma)$vectors)
  sqrt(diag(lamda))
  lamda_sqrt <- matrix(c(sqrt(diag(lamda))[1],0,0,0,sqrt(diag(lamda)[2]),0, 0, 0, sqrt(diag(lamda)[3])),nrow = 3,ncol = 3)
  Sigma_sqrt <- (eigen(Sigma)$vectors)%*%lamda_sqrt%*%solve(eigen(Sigma)$vectors)  
  return(solve(Sigma_sqrt))
}

A2 = fuermi(CorX) %*% CorXY %*% solve(CorY) %*% CorYX %*% fuermi(CorX)
B2 = fuermi(CorY) %*% CorYX %*% solve(CorX) %*% CorXY %*% fuermi(CorY)

e1 = eigen(A2)$vectors
e2 = eigen(B2)$vectors

rho1 = eigen(B2)$values[1]
rho2 = eigen(B2)$values[2]
rho3 = eigen(B2)$values[3]

# 典型相关系数
c(rho1, rho2, rho3)

1. 1.2116851534277
2. 0.229934013998988
3. 0.0274354332393604

## X的典型相关变量系数
e1

A matrix: 3 × 3 of type dbl

-0.3287070	0.2380847	0.9139296
-0.3796076	-0.9193985	0.1029784
-0.8647831	0.3130849	-0.3925915

## Y的典型相关变量系数
e2

A matrix: 3 × 3 of type dbl

-0.60894743	-0.2898345	0.7383624
0.04600424	-0.9421908	-0.3319037
-0.79187539	0.1681441	-0.5870783

  希望我的文章对您有所帮助，同时也感谢您能抽出宝贵的时间阅读，打公式不易，如果您喜欢的话，欢迎点赞、关注、收藏。您的支持是我创作的动力，希望今后能带给大家更多优质的文章