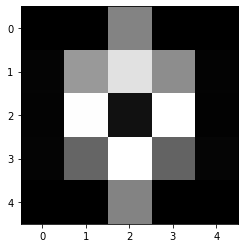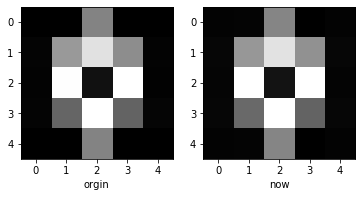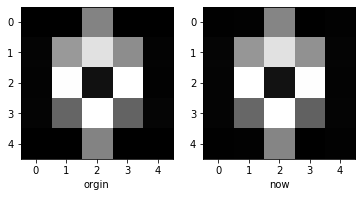使用特征值分解和SVD分解处理图片矩阵并还原重构矩阵
使用特征值分解和SVD分解处理图片矩阵并还原重构矩阵
- 1. 模块导入和图片预处理
- 1.1 导入模块
- 1.2 加载和处理图片
- 1.3 查看图片数组和显示图片
- 2. 小型矩阵测试
- 2.1 使用特征值分解
- 2.2 使用奇异值分解
- 3. 正式图片处理
- 3.1 我们先来尝试用特征值分解
- 3.2 SVD分解并还原重构矩阵
1. 模块导入和图片预处理
1.1 导入模块
#导入绘图模块和矩阵处理模块
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
1.2 加载和处理图片
#定义图片处理函数
def loadImage(url):
# 读取图片
im = Image.open(url)
#灰度化
im = im.convert("L")
#将图片生成数组
image_data = np.asarray(im)
return image_data
image_data = loadImage("images/pic03.jpg")
1.图像转换为矩阵 matrix = numpy.asarray(image)
2.矩阵转换为图像 image = Image.fromarray(matrix)
1.3 查看图片数组和显示图片
image_data
array([[161, 161, 161, ..., 168, 152, 131],
[161, 161, 160, ..., 169, 155, 133],
[161, 160, 160, ..., 170, 154, 129],
...,
[ 48, 48, 49, ..., 99, 100, 101],
[ 48, 48, 49, ..., 102, 105, 107],
[ 48, 48, 49, ..., 105, 108, 111]], dtype=uint8)
image_data.shape
(512, 512)
plt.imshow(image_data,cmap='gray')
2. 小型矩阵测试
2.1 使用特征值分解
#测试用的矩阵
demo_data = np.array([[1,1,130,1,1],[5,150,220,139,4],[4,249,18,250,3],[5,100,250,98,6],[1,1,130,1,1]])
plt.imshow(demo_data,cmap='gray')
#求特征值和特征向量
cvalue,cvector = np.linalg.eig(demo_data)
cvalue
array([ 4.94008077e+02, -2.29280772e+02, -2.42519807e+00, 8.69697506e-15,
5.69789288e+00])
cvector
array([[-0.15591872, -0.3807619 , 0.69881489, 0.8992716 , 0.32946326],
[-0.58591235, -0.22576077, 0.09769686, -0.06501486, -0.63170598],
[-0.58159929, 0.68252499, -0.02365501, -0.00354707, 0.00946567],
[-0.51944941, -0.43958216, -0.11494025, 0.05576873, 0.6194884 ],
[-0.15591872, -0.3807619 , 0.69881489, -0.42890667, 0.32946326]])
#定义根据特征值还原的函数
def restore(cvector,cvalue, n, N):
#求逆矩阵
cvector1 = np.linalg.inv(cvector)
#取前n个特征值，生成对角阵
dia = np.append(cvalue[0:n],np.zeros(N-n))
lam_new = np.diag(dia)
#还原矩阵
now_image = np.dot(np.dot(cvector,lam_new),cvector1)
return now_image
- 选全部特征值还原
restore(cvector,cvalue,5,5)
array([[ 1., 1., 130., 1., 1.],
[ 5., 150., 220., 139., 4.],
[ 4., 249., 18., 250., 3.],
[ 5., 100., 250., 98., 6.],
[ 1., 1., 130., 1., 1.]])
- 选前2个特征值还原
w2 = restore(cvector,cvalue,2,5)
w2
array([[ 1.76315344, 2.59799271, 130.01669759, -1.36543068,
2.0501414 ],
[ 5.13361385, 146.93056126, 220.9469344 , 141.06003781,
5.00544282],
[ 3.97334813, 249.046078 , 17.97069947, 250.00734266,
2.9383325 ],
[ 4.84771757, 103.01014683, 249.05835103, 96.01274961,
4.97382364],
[ 1.76315344, 2.59799271, 130.01669759, -1.36543068,
2.0501414 ]])
plt.subplot(1,2,1)
plt.imshow(demo_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(w2,cmap='gray')
plt.xlabel("now")
- 发现还原的图片基本上保留了原图的特征
2.2 使用奇异值分解
U,Sigma,V = np.linalg.svd(demo_data, full_matrices=1)
Sigma
array([5.04623689e+02, 2.76409192e+02, 5.80069732e+00, 2.05978309e+00,
2.19076549e-15])
注意这里的sigma矩阵是一维矩阵，还原时首先要生成其作为对角线的对角阵
#定义svd恢复函数
def resvd(U,Sigma,V,n):
si = np.diag(Sigma[0:n])
return U[:,:n]@si@V[:n,:]
#100%还原
w3 = resvd(U,Sigma,V,5)
w3
array([[ 1., 1., 130., 1., 1.],
[ 5., 150., 220., 139., 4.],
[ 4., 249., 18., 250., 3.],
[ 5., 100., 250., 98., 6.],
[ 1., 1., 130., 1., 1.]])
plt.imshow(w3,cmap='gray')
#取前两个奇异值还原
w4 = resvd(U,Sigma,V,2)
w4
array([[ 1.53122803e+00, 2.16367311e+00, 1.29961911e+02,
-1.86885877e-01, 1.78340172e+00],
[ 4.90249998e+00, 1.46825833e+02, 2.20049100e+02,
1.42182436e+02, 4.69011577e+00],
[ 4.24435786e+00, 2.50235873e+02, 1.79725146e+01,
2.48752501e+02, 3.16301924e+00],
[ 4.51593381e+00, 1.01495187e+02, 2.49998359e+02,
9.65225041e+01, 4.56633464e+00],
[ 1.53122803e+00, 2.16367311e+00, 1.29961911e+02,
-1.86885877e-01, 1.78340172e+00]])
plt.subplot(1,2,1)
plt.imshow(demo_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(w4,cmap='gray')
plt.xlabel("now")
- 发现还原效果与原图几乎一样，可能是原图像素比较低，接下来我们处理像素高、信息多的图片
3. 正式图片处理
通过查阅资料：
- 特征分解相比奇异值分解其应用条件要苛刻得多，特征分解要求矩阵与对角矩阵(可对角化)相似,这在图像上一般是不满足的
- 而奇异值分解适用于任何矩阵，应用范围也就更加广泛，但是奇异值分解本身时间复杂度相当高，随着矩阵规模的增长，计算复杂度将呈立方增长
3.1 我们先来尝试用特征值分解
#先看看我们要处理的图片
plt.imshow(image_data,cmap='gray')
# 计算特征值和特征向量
cha_value,cha_vector = np.linalg.eig(image_data)
cha_value
array([ 6.31940689e+04+0.00000000e+00j, -8.03929061e+03+0.00000000e+00j,
5.27031308e+03+0.00000000e+00j, -4.35274045e+03+0.00000000e+00j,
1.31653780e+03+2.64437231e+03j, 1.31653780e+03-2.64437231e+03j,
......
4.58561787e-01+9.28776882e-02j, 4.58561787e-01-9.28776882e-02j,
5.59703226e-02+3.78031829e-01j, 5.59703226e-02-3.78031829e-01j,
-1.72117496e-01+3.89324226e-01j, -1.72117496e-01-3.89324226e-01j])
cha_value.shape
(512,)
cha_vector
array([[-0.04870187+0.j , 0.00148652+0.j ,
0.03914127+0.j , ..., -0.01392511-0.08843148j,
0.04003832+0.00911842j, 0.04003832-0.00911842j],
[-0.04869858+0.j , 0.00147211+0.j ,
0.03903883+0.j , ..., 0.01722793+0.03851178j,
-0.03756849-0.03310897j, -0.03756849+0.03310897j],
[-0.04869473+0.j , 0.00143451+0.j ,
0.03884124+0.j , ..., -0.00707275-0.0008019j ,
0.07088382-0.01090998j, 0.07088382+0.01090998j],
...,
[-0.04148487+0.j , 0.06893779+0.j ,
-0.00943626+0.j , ..., -0.00072898+0.0444966j ,
-0.08156037-0.08678486j, -0.08156037+0.08678486j],
[-0.04139138+0.j , 0.07030029+0.j ,
-0.01074787+0.j , ..., 0.09199783-0.06395806j,
0.07602846+0.02662019j, 0.07602846-0.02662019j],
[-0.04130632+0.j , 0.07137667+0.j ,
-0.01183001+0.j , ..., -0.05014964+0.02169388j,
-0.00777808+0.01356449j, -0.00777808-0.01356449j]])
cha_vector.shape
(512, 512)
- 由于特征值存在复数，而python 不支持复数转换为整数或浮点数，所以接下来采用奇异值分解
3.2 SVD分解并还原重构矩阵
U,Sigma,V = np.linalg.svd(image_data, full_matrices=1)
Sigma
array([6.47863129e+04, 1.06097179e+04, 8.15616672e+03, 6.48027847e+03,
5.88171483e+03, 5.53885283e+03, 4.57280722e+03, 4.08863670e+03,
3.36892938e+03, 3.15843979e+03, 2.65792456e+03, 2.44007735e+03,
......
3.10658340e-01, 2.66331019e-01, 2.45874463e-01, 2.29508349e-01,
2.09154136e-01, 1.72908417e-01, 1.50184655e-01, 9.61525803e-02,
8.22379370e-02, 6.02098344e-02, 3.84692480e-02, 1.32001603e-02])
#定义列表，元素为取数量从10到180,间隔为20个奇异值还原的矩阵
resvd_image = []
for i in range(10,180,20):
resvd_image.append(resvd(U,Sigma,V,i))
#取前10个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[0],cmap='gray')
plt.xlabel("have 10 singular values")
#取前30个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[1],cmap='gray')
plt.xlabel("have 30 singular values")
#取前50个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[2],cmap='gray')
plt.xlabel("have 50 singular values")
#取前70个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[3],cmap='gray')
plt.xlabel("have 70 singular values")
#取前90个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[4],cmap='gray')
plt.xlabel("have 90 singular values")
#取前170个奇异值还原
plt.subplot(1,2,1)
plt.imshow(image_data,cmap='gray')
plt.xlabel("orgin")
plt.subplot(1,2,2)
plt.imshow(resvd_image[8],cmap='gray')
plt.xlabel("have 170 singular values")
- 我们发现只要取少量奇异值（大概50到70个奇异值）就能保留原图片中大部分信息