人工智能--遗传算法(旅行商问题)
人工智能是研究使计算机来模拟人的某些思维过程和智能行为(如学习、推理、思考、规划等)的学科,主要包括计算机实现智能的原理、制造类似于人脑智能的计算机,使计算机能实现更高层次的应用。人工智能将涉及到计算机科学、心理学、哲学和语言学等学科。可以说几乎是自然科学和社会科学的所有学科,其范围已远远超出了计算机科学的范畴,人工智能与思维科学的关系是实践和理论的关系,人工智能是处于思维科学的技术应用层次,是它的一个应用分支。从思维观点看,人工智能不仅限于逻辑思维,要考虑形象思维、灵感思维才能促进人工智能的突破性的发展,数学常被认为是多种学科的基础科学,数学也进入语言、思维领域,人工智能学科也必须借用数学工具,数学不仅在标准逻辑、模糊数学等范围发挥作用,数学进入人工智能学科,它们将互相促进而更快地发展。
遗传算法是计算数学中用于解决最佳化的搜索算法,是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等。遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题,一定数量的候选解(称为个体)的抽象表示(称为染色体)的种群向更好的解进化。传统上,解用二进制表示(即0和1的串),但也可以用其他表示方法。进化从完全随机个体的种群开始,之后一代一代发生。在每一代中,整个种群的适应度被评价,从当前种群中随机地选择多个个体(基于它们的适应度),通过自然选择和突变产生新的生命种群,该种群在算法的下一次迭代中成为当前种群。
- 上机题简介
-
用C++语言编写和调试一个用遗传算法解旅行商TSP问题的程序。目的是学会运用知识表示方法和搜索策略求解一些考验智力的简单问题,熟悉简单智能算法的开发过程并理解其实现原理。
用遗传算法解旅行商TSP问题:假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
在遗传算法解旅行商TSP问题当中程序总体围绕了遗传算法的三个主要步骤:选择--复制,交叉,变异。给定了10个种群,即10条染色体,每条染色体都是除首位外不重复的点组成,首尾相同保证路线是闭合的,所以一条染色体包含11个点。
遗传算法解旅行商TSP问题实验原理:
TSP问题就是寻找一条最短的遍历n个城市的最短路径,即搜索自然数子集W={1,2..n}(W的元素表示对n个城市的编号)的一个排列。
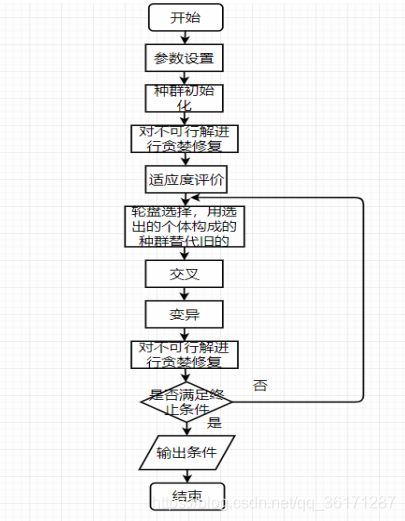
遗传算法是具有“生成+检测”的迭代过程的搜索算法。它的基本处理流程如图1所示。由此流程图可见,遗传算法是一种群体型操作,该操作以群体中的所有个体为对象。选择( Selection)、交叉(Crossover)和变异(Mutation) 是遗传算法的3个主要操作算子,它们构成了所谓的遗传操作( genetic operation),使遗传算法具有了其它传统方法所没有的特性。遗传算子包含如下6个基本因素:
(1)参数编码:由于遗传算法不能直接处理解空间的解数据,因此必须通过编码将它们表示成遗传空间的基因型串结构数据。
(2)生成初始群体:由于遗传算法的群体型操作需要,所以必须为遗传操作准备一个由若干初始解组成的初始群体。初始群体的每个个体都是通过随机方法产生。
( 3)适应度评估检测:遗传算法在搜索进化过程中一般不需要其他外部信息,仅用适应度( fitness) 值来评估个体或解的优劣,并作为以后遗传操作的依据。
(4)选择(selection): 选择或复制操作是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。个体适应度越高,其被选择的机会就越多。此处采用与适用度成比例的概率方法进行选择。具体地说,就是首先计算群体中所有个体适应度的总和,再计算每个个体的适应度所占的比例,并以此作为相应的选择概率。
(5)交叉操作:交叉操作是遗传算法中最主要的遗传操作。简单的交叉(即一点交叉)可分两步进行:首先对种群中个体进行随机配对:其次,在配对个体中随机设定交叉处,配对个体彼此交换部分信息。
(6)变异:变异操作是按位(bit) 进行的,即把某一位的内容进行变异。变异操作同样也是随机进行的。一般而言,变异概率P都取得较小。变异操作是十分微妙的遗传操作,它需要和交叉操作配合使用,目的是挖掘群体中个体的多样性,克服有可能限于局部解的弊病。
遗传算法解旅行商TSP问题程序功能结构图:
流程图:
数据结构定义:
//定义染色体的结构
struct Chrom
{
int cityArr[cityNum]; //染色体的基因编码
char name; //染色体的名称
float adapt; //染色体的适应度
int dis; //染色体的路径长度
};
struct Chrom genes[popSize]; //定义基因库(结构体数组)
struct Chrom genesNew[popSize]; //重新建立一个新的种群
struct Chrom temp; //定义临时公用结点
names[cityNum] = {'A','B','C','D','E','F','G','H','I','J'}; //城市名称
distance[cityNum][cityNum] //城市距离矩阵
函数方法定义:
initGroup() //初始化基因库
popFitness() //计算种群所有染色体的个体适应度
chooseBest() //返回最优秀的一条染色体
select() // 选择操作
cross() //交叉操作
mutation() //变异操作
遗传算法解旅行商TSP问题C语言代码:
#include "stdio.h"
#include "stdlib.h"
#include "windows.h"
#include "time.h"
#define cityNum 10 //城市数量(基因数量)(染色体长度)
#define popSize 10 //种群大小(尺寸)
#define croRate 0.85 //交叉概率
#define mutRate 0.1 //变异概率
#define MAX 999 //进化代数
//定义染色体的结构
struct Chrom
{
int cityArr[cityNum]; //染色体的基因编码
char name; //染色体的名称
float adapt; //染色体的适应度
int dis; //染色体的路径长度
};
struct Chrom genes[popSize]; //定义基因库(结构体数组)
struct Chrom genesNew[popSize]; //重新建立一个新的种群
struct Chrom temp; //定义临时公用结点
char names[cityNum] = {'A','B','C','D','E','F','G','H','I','J'}; //城市名称
int distance[cityNum][cityNum] = {{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }, //城市距离矩阵
{ 1, 0, 1, 2, 3, 4, 5, 6, 7, 8 },
{ 2, 1, 0, 1, 2, 3, 4, 5, 6, 7 },
{ 3, 2, 1, 0, 1, 2, 3, 4, 5, 6 },
{ 4, 3, 2, 1, 0, 1, 2, 3, 4, 5 },
{ 5, 4, 3, 2, 1, 0, 1, 2, 3, 4 },
{ 6, 5, 4, 3, 2, 1, 0, 1, 2, 3 },
{ 7, 6, 5, 4, 3, 2, 1, 0, 1, 2 },
{ 8, 7, 6, 5, 4, 3, 2, 1, 0, 1 },
{ 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }}; //最优解为18
void initGroup()
{
//初始化基因库
int i,j,k;
int t = 0;
int flag = 0;
srand(time(NULL));//初始化随机种子,防止随机数每次重复,常常使用系统时间来初始化,当srand()的参数值固定的时候,rand()获得的数也是固定的
for(i = 0; i < popSize; i ++)
{
//使用临时结点开始赋值
temp.name = names[i];
temp.adapt = 0.0f;
temp.dis = 0;
//产生10个不相同的数字
for(j = 0; j < cityNum;)
{
t = rand()%cityNum; //随机产生0-9的数
flag = 1;
for(k = 0; k < j; k ++)
{
if(genes[i].cityArr[k] == t)
{
flag = 0;
break;
}
}
if(flag)
{
temp.cityArr[j] = t;
genes[i] = temp;//存入结构体数组,产生一个个体
j++;
}
}
}
}
//计算种群所有染色体的个体适应度
void popFitness()
{
int i,n1,n2;
for(i = 0; i < popSize; i ++)
{
genes[i].dis = 0;
for(int j = 1;j < cityNum; j ++)
{
n1 = genes[i].cityArr[j-1];
n2 = genes[i].cityArr[j];
genes[i].dis += distance[n1][n2];
}
genes[i].dis += distance[genes[i].cityArr[0]][genes[i].cityArr[cityNum-1]];
genes[i].adapt = (float)1/genes[i].dis; //每条染色体的路径总和(个体适应度)
}
}
//返回最优秀的一条染色体
int chooseBest()
{
int choose = 0;
float best = 0.0f;
best = genes[0].adapt;
for(int i = 0; i < popSize; i ++)
{
if(genes[i].adapt < best)
{
best = genes[i].adapt;
choose = i;
}
}
return choose;
}
// 选择操作
void select()
{
float biggestSum = 0.0f;
float adapt_pro[popSize];
float pick = 0.0f;
int i;
for(i = 0; i < popSize; i ++)
{
biggestSum += genes[i].adapt; // 总概率
}
for(i = 0; i < popSize; i ++)
{
adapt_pro[i] = genes[i].adapt / biggestSum; // 概率数组
}
// 轮盘赌
for(i = 0;i < popSize; i ++)
{
pick = (float)rand()/RAND_MAX; // 0到1之间的随机数
for(int j = 0; j < popSize; j ++)
{
pick = pick - adapt_pro[j];
if(pick <= 0)
{
genesNew[i] = genes[j];
break;
}
}
}
for(i = 0;i < popSize; i++)
{
genes[i] = genesNew[i];
}
}
void cross() // 交叉操作
{
float pick;
int choice1,choice2;
int pos1,pos2;
int temp;
int conflict1[popSize]; // 冲突位置
int conflict2[popSize];
int num1;
int num2;
int index1,index2;
int move = 0; // 当前移动的位置
while(move < popSize-1)
{
pick = (float)rand()/RAND_MAX; // 用于决定是否进行交叉操作
if(pick > croRate) //两条染色体是否相爱
{
move += 2;
continue; // 本次不进行交叉
}
// 采用部分映射杂交
choice1 = move; // 用于选取杂交的两个父代
choice2 = move+1; // 注意避免下标越界
pos1 = rand()%popSize;
pos2 = rand()%popSize;
while(pos1 > popSize -2 || pos1 < 1)//如果位置在开头或结尾(因为全部交换无意义)
{
pos1 = rand()%popSize;
}
while(pos2 > popSize -2 || pos2 < 1)
{
pos2 = rand()%popSize;
}
if(pos1 > pos2)
{
temp = pos1;
pos1 = pos2;
pos2 = temp; // 交换pos1和pos2的位置
}
for(int j = pos1;j <= pos2; j++)// 逐个交换顺序
{
temp = genes[choice1].cityArr[j];
genes[choice1].cityArr[j] = genes[choice2].cityArr[j];
genes[choice2].cityArr[j] = temp;
}
num1 = 0;
num2 = 0;
if(pos1 > 0 && pos2 < popSize - 1)//分三段
{
for(int j =0;j < pos1;j++)
{
for(int k = pos1; k <= pos2; k++)
{
if(genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
{
conflict1[num1] = j;
num1 ++;
}
if(genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
{
conflict2[num2] = j;
num2 ++;
}
}
}
for(j = pos2 + 1;j < popSize;j++)
{
for(int k = pos1; k <= pos2; k ++)
{
if(genes[choice1].cityArr[j] == genes[choice1].cityArr[k])
{
conflict1[num1] = j;
num1 ++;
}
if(genes[choice2].cityArr[j] == genes[choice2].cityArr[k])
{
conflict2[num2] = j;
num2 ++;
}
}
}
}
if((num1 == num2) && num1 > 0)
{
for(int j = 0;j < num1; j ++)
{
index1 = conflict1[j];
index2 = conflict2[j];
temp = genes[choice1].cityArr[index1]; // 交换冲突的位置
genes[choice1].cityArr[index1] = genes[choice2].cityArr[index2];
genes[choice2].cityArr[index2] = temp;
}
}
move += 2;
}
}
//变异操作
void mutation()
{
double pick;
int pos1,pos2,temp;
for(int i = 0;i < popSize; i ++)
{
pick = (float)rand()/RAND_MAX; // 用于判断是否进行变异操作
if(pick > mutRate)
{
continue;
}
pos1 = rand()%popSize;
pos2 = rand()%popSize;
while(pos1 > popSize - 1)
{
pos1 = rand()%popSize;
}
while(pos2 > popSize - 1)
{
pos2 = rand()%popSize;
}
int a = genes[i].dis;
temp = genes[i].cityArr[pos1];
genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
genes[i].cityArr[pos2] = temp;
popFitness();//更新数据
//此步骤的作用在于检查是否变异后得到的个体比变异前更优秀了,如若往坏的方向变化了,那还不如不变异了
//(强制返回,虽然有点违背事物的客观发展规律,但为了增强程序的收敛性,该操作还是有必要的)(偷笑)
if(genes[i].dis > a)
{
temp = genes[i].cityArr[pos1];
genes[i].cityArr[pos1] = genes[i].cityArr[pos2];
genes[i].cityArr[pos2] = temp;
}
}
}
int main()
{
char c = 0;
printf("\n\t\t******************************** 遗传算法求解TSP(旅行商)问题 *********************************\n");
initGroup(); //初始化
popFitness(); //更新数据
//输出配置信息
printf("\n\t\t基因长度:%d",cityNum);
printf("\t种群大小:%d",popSize);
printf("\t交叉概率:%.2f",croRate);
printf("\t变异概率:%.2f",mutRate);
printf("\t进化代数:%d",MAX);
printf("\t预设最优解:18");
printf("\n\n\t\t**********************************************************************************************\n");
//输出距离矩阵
printf("\n\n\t\t--------- 城市距离矩阵 ---------\n");
printf("\t\t");
int i,j;
for(i = 0; i < cityNum; i ++)
{
for(j = 0;j < cityNum; j ++)
{
printf(" %d",distance[i][j]);
}
printf("\n\t\t");
}
printf("--------------------------------\n");
//输出路径信息
printf("\n\t\t-------- 初始种群基因库 --------\n");
printf("\t\t ");
for(i = 0; i < cityNum; i ++)
{
printf(" %c",genes[i].name);
}
printf("\n\t\t");
for(i = 0;i < cityNum; i ++)
{
printf("%c",genes[i].name);
for(j = 0; j < cityNum; j ++)
{
printf(" %d",genes[i].cityArr[j]);
}
printf("\n\t\t");
}
printf("--------------------------------\n");
do
{
printf("\n\t\t寻求最优解中:");
//通过不断进化,直到达到定义的进化代数
for(i = 0; i < MAX; i ++)
{
select();
cross();
popFitness();//更新数据
mutation();
popFitness();//更新数据
int temp = (int)MAX/20;
}
printf("完成");
printf("\n\n\t\t最优路径:");
for(i = 0; i < cityNum ; i++)
{
printf("%d-->",genes[chooseBest()].cityArr[i]);
}
printf("%d",genes[chooseBest()].cityArr[0]);
printf("\n\n\t\t路径长度:%d",genes[chooseBest()].dis);
printf("\n\n\t\t是否再试一次?(Y/y) 是/(N/n) 否:");
fflush(stdin);
c = getchar();
fflush(stdin);
if(c=='N'||c=='n')
{
break;
}
}while(1);
printf("\n\t\t");
return 0;
}
- 总结体会
在旅行商问题当中由遗传算法对以上情况的求解(10座城市),可以看出,用传算法来求解TSP问题是可行的。用遗传算法求解时,增加选代次数,可以得到更加优良的结果,但是会需要更长的时间,即一个优良的结果往往是以时间力代价的,这种情况要依据具体问题具体分析,平衡两者在问题求解时的比重。参数设置得好坏往往对遗传算法的性能和结果有着重要的影响,往往在解决某一问题的时候,需要设定的参数很多,如何获得最佳的参数组合是一个很重要的问题。另外,对选择算法进行优化,会提高遗传算法的性能,这些都需要在实践中不断科累和广泛涉猎优良算法。最后,遗传算法得到的未必是最优解,我们可以根据需要进行多次求解,从而比较得出符合要求的结果。