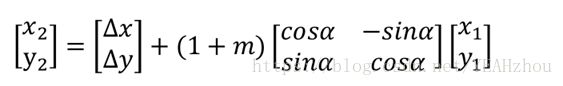【坐标转换】四参数和七参数计算（真正代码实现）

实际项目中，经常遇到到不同坐标系之间变换的需求，比如西安80转wgs84，再转成百度坐标用于web显示。但网上只有不同椭球基准坐标系之间转换的片段资料或代码，本文将尽量展示出更多的核心代码（涉及变换的整个流程），供大家参考。

---

四参数计算

四参数变换模式主要用于范围较小平面坐标变换，四参数计算需要两个以上的参考原点。

四参数类

public class FourParam implements ParamCalculator {
    /**
     * x轴偏移
     */
    private double dx;
    /**
     * y轴偏移
     */
    private double dy;
    /**
     * 形变因子 1+m
     */
    private double scale;
    /**
     * 转角 单位:度
     */
    private double rotate;



    ....seter()
    ....geter()
}

计算（核心）

在地图选择两个以上的公共参考点，以公共参考的原始坐标对（西安80）和转换的目标坐标对（四川本地）为输入参数，计算出四参数。

public void calculate(GaussCoordinate[] p1, GaussCoordinate[] p2) {
        if (p1.length != p2.length) {
            throw new IllegalArgumentException(" The two sets of coordinates are different in number");
        }
        if (p1.length < 2) {
            throw new NullPointerException("The number of point is 0. At least one pair of coordinate points");
        }

        double u = 1.0, v = 0, Dx = 0.0, Dy = 0.0;
        int intCount = p1.length;
        double[][] B1 = new double[2 * intCount][4];
        double[][] W1 = new double[2 * intCount][1];

        for (int i = 0; i < intCount; i++) {
            //计算误差方程系数
            B1[2 * i][0] = 1;
            B1[2 * i][1] = 0;
            B1[2 * i][2] = p1[i].x_B();
            B1[2 * i][3] = -p1[i].y_L();

            B1[2 * i + 1][0] = 0;
            B1[2 * i + 1][1] = 1;
            B1[2 * i + 1][2] = p1[i].y_L();
            B1[2 * i + 1][3] = p1[i].x_B();
        }
        Matrix B = new Matrix(B1);//误差方程系数矩阵

        for (int i = 0; i < intCount; i++) {
            //计算误差方程系常数
            W1[2 * i][0] = p2[i].x_B() - u * p1[i].x_B() + v * p1[i].x_B() - Dx;
            W1[2 * i + 1][0] = p2[i].y_L() - u * p1[i].y_L() - v * p1[i].x_B() - Dy;
        }
        Matrix W = new Matrix(W1); //误差方程常数项

        //最小二乘求解
        Matrix BT = B.transpose();
        Matrix N = BT.times(B);
        Matrix InvN = N.inverse();
        Matrix BTW = BT.times(W);
        Matrix dx1 = InvN.times(BTW); //误差方程改正数

        DecimalFormat df = new DecimalFormat("0.0000000");
        this.dx = Double.valueOf(df.format(Dx + dx1.get(0, 0)));
        this.dy = Double.valueOf(df.format(Dy + dx1.get(1, 0)));
        u = u + dx1.get(2, 0);//(1+m)cos&
        v = v + dx1.get(3, 0);//(1+m)sin&
        this.rotate = Double.valueOf(df.format(Math.atan(v / u)));
        this.scale = Double.valueOf(df.format(u / Math.cos(rotate)));
}

矩阵运算使用的jar包依赖：

      gov.nist.math
      jama
      1.0.3

坐标转换

计算出四参数后，就可以利用公式将原始坐标系转换成目标坐标系

public static GaussCoordinate transformPlaneCoordinate(GaussCoordinate sourceCoordinate, FourParam fourParam) {
        double x = sourceCoordinate.x_B(), y = sourceCoordinate.y_L();
        double a = fourParam.getScale() * Math.cos(fourParam.getRotate());
        double b = fourParam.getScale() * Math.sin(fourParam.getRotate());

        double targetX = fourParam.getDx() + a * x - b * y;
        double targetY = fourParam.getDy() + b * x + a * y;
        //椭球体参数使用目标椭球体
        GaussCoordinate gaussTarget= new GaussCoordinate(sourceCoordinate.getNo(),targetX, targetY,
                sourceCoordinate.z_H(),fourParam.getTargetProjNum(),fourParam.getTargetProjType(),fourParam.targetEllipsoid());
        return gaussTarget;
}

---

七参数计算

两个空间直角坐标系进行转换计算就需要用到七个参数，即不同椭球体之间的坐标系变换。

以西安80经纬度坐标转wgs84高斯平面坐标为例

首先将公共参考点（三对以上）的源经纬度坐标，以及目标高斯平面坐标均转换为空间直角坐标

经纬度坐标转空间直角坐标

/**
     * 大地坐标系换换成空间直角坐标系
     *
     * @param ellipsoid 椭球体
     * @return
     */
public static SpaceCoordinate BLHtoXYZ(BLHCoordinate coordinate, Ellipsoid ellipsoid) {
        double L = coordinate.L_longitude(), B = coordinate.B_latitude(), H = coordinate.H_height();
        double dblD2R = Math.PI / 180;
        double aAxis = ellipsoid.getMacroAxis(), bAxis = ellipsoid.getMinorAxis();
        double e1 = Math.sqrt(Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / aAxis;
        double N = aAxis / Math.sqrt(1.0 - Math.pow(e1, 2) * Math.pow(Math.sin(B * dblD2R), 2));

        double X = (N + H) * Math.cos(B * dblD2R) * Math.cos(L * dblD2R);
        double Y = (N + H) * Math.cos(B * dblD2R) * Math.sin(L * dblD2R);
        double Z = (N * (1.0 - Math.pow(e1, 2)) + H) * Math.sin(B * dblD2R);
        return new SpaceCoordinate(coordinate.getNo(),X, Y, Z,coordinate.projNum(),coordinate.projType(),coordinate.ellipsoid());
}

高斯平面坐标转空间直角坐标

/**
     * 空间直接坐标系转换为大地坐标系
     *
     * @param ellipsoid 椭球体
     * @return
     */
public static BLHCoordinate XYZtoBLH(SpaceCoordinate coordinate, Ellipsoid ellipsoid) {
        double X = coordinate.X(), Y = coordinate.Y(), Z = coordinate.Z();
        double aAxis = ellipsoid.getMacroAxis(), bAxis = ellipsoid.getMinorAxis();
        double e1 = (Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / Math.pow(aAxis, 2);
        double e2 = (Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / Math.pow(bAxis, 2);

        double S = Math.sqrt(Math.pow(X, 2) + Math.pow(Y, 2));
        double cosL = X / S;
        double B = 0;
        double L = 0;

        L = Math.acos(cosL);
        L = Math.abs(L);

        double tanB = Z / S;
        B = Math.atan(tanB);
        double c = aAxis * aAxis / bAxis;
        double preB0 = 0.0;
        double ll = 0.0;
        double N = 0.0;
        //迭代计算纬度
        do {
            preB0 = B;
            ll = Math.pow(Math.cos(B), 2) * e2;
            N = c / Math.sqrt(1 + ll);

            tanB = (Z + N * e1 * Math.sin(B)) / S;
            B = Math.atan(tanB);
        }
        while (Math.abs(preB0 - B) >= 0.0000000001);

        ll = Math.pow(Math.cos(B), 2) * e2;
        N = c / Math.sqrt(1 + ll);

        double targetH = Z / Math.sin(B) - N * (1 - e1);
        double targetB = B * 180 / Math.PI;
        double targetL = L * 180 / Math.PI;
        return new BLHCoordinate(coordinate.getNo(),targetL, targetB, targetH,coordinate.projType(),ellipsoid.getId());
}

然后计算七参数

/**
     * 计算空间直角坐标系
     * @param p1
     * @param p2
     */
public void  calculate(SpaceCoordinate[] p1, SpaceCoordinate[] p2) {
        if (p1.length != p2.length) {
            throw new IllegalArgumentException(" The two sets of coordinates are different in number");
        }
        if (p1.length < 3 ) {
            throw new NullPointerException(" At least 3 pair of coordinate points");
        }
        int pointCount = p1.length;
        double[][] B = new double[pointCount * 3][7];
        double[][] L = new double[pointCount * 3][1];
        //初始化L矩阵
        for (int i = 0; i < pointCount * 3; i++) {
            if (i % 3 == 0) {
                L[i][0] = p2[i / 3].X();
            } else if (i % 3 == 1) {
                L[i][0] = p2[i / 3].Y();
            } else if (i % 3 == 2) {
                L[i][0] = p2[i / 3].Z();
            }
        }
        //初始化B矩阵
        for (int i = 0; i < pointCount * 3; i++) {
            if (i % 3 == 0) {
                B[i][0] = 1;
                B[i][1] = 0;
                B[i][2] = 0;
                B[i][3] = p1[i / 3].X();
                B[i][4] = 0;
                B[i][5] = -p1[i / 3].Z();
                B[i][6] = p1[i / 3].Y();

            } else if (i % 3 == 1) {
                B[i][0] = 0;
                B[i][1] = 1;
                B[i][2] = 0;
                B[i][3] = p1[i / 3].Y();
                B[i][4] = p1[i / 3].Z();
                B[i][5] = 0;
                B[i][6] = -p1[i / 3].X();
            } else if (i % 3 == 2) {
                B[i][0] = 0;
                B[i][1] = 0;
                B[i][2] = 1;
                B[i][3] = p1[i / 3].Z();
                B[i][4] = -p1[i / 3].Y();
                B[i][5] = p1[i / 3].X();
                B[i][6] = 0;
            }

        }
        Matrix bM = new Matrix(B);
        Matrix lM = new Matrix(L);
        //转置
        Matrix bt = bM.transpose();
        //法方程矩阵
        //N=BT*B
        Matrix n = bt.times(bM);
        //求逆
        Matrix invN = n.inverse();
        //BTL=BT*L
        Matrix btl = bt.times(lM);
        //dx1=invN*BTL;
        Matrix dx = invN.times(btl);

        DecimalFormat df = new DecimalFormat("0.0000000");
        xOffset =Double.valueOf(df.format(dx.get(0, 0))) ;
        yOffset =Double.valueOf(df.format(dx.get(1, 0))) ;
        zOffset = Double.valueOf(df.format(dx.get(2, 0)));
        scale = Double.valueOf(df.format(dx.get(3, 0)));//(a1=m+1)
        xRotate = Double.valueOf(df.format(dx.get(4, 0)/scale));
        yRotate = Double.valueOf(df.format(dx.get(5, 0)/scale));
        zRotate = Double.valueOf(df.format(dx.get(6, 0)/scale));
}

坐标转换

计算出七参数后，就可以对不同椭球体的空间直角坐标进行转换，然后变换成经纬度坐标或平面坐标

/**
     * 空间直角坐标七参转换
     *
     * @param sourceCoordinate
     * @return
     */

public static SpaceCoordinate transformSpaceCoordinate(SpaceCoordinate sourceCoordinate,SevenParam sevenParam) {
        double X = sourceCoordinate.X(), Y = sourceCoordinate.Y(), Z = sourceCoordinate.Z();
        double Ex, Ey, Ez;
        Ex = sevenParam.xRotate() *sevenParam.scale();
        Ey = sevenParam.yRotate()*sevenParam.scale() ;
        Ez = sevenParam.zRotate()*sevenParam.scale() ;

        double targetX = sevenParam.xOffset() + sevenParam.scale() * X + Y * Ez - Z * Ey ;
        double targetY = sevenParam.yOffset() + sevenParam.scale() * Y - X * Ez + Z * Ex ;
        double targetZ = sevenParam.zOffset() + sevenParam.scale() * Z + X * Ey - Y * Ex ;
        //椭球体参数使用目标椭球体
        return new SpaceCoordinate(sourceCoordinate.getNo(),targetX, targetY, targetZ,sevenParam.getTargetProjNum(),
                sevenParam.getTargetProjType(),sevenParam.targetEllipsoid());
}