Opencv图像插值算法与其应用（图像伸缩）

DataWhale 机器视觉组队学习task1

1.1 简介

  在图像处理中，平移变换、旋转变换以及放缩变换是一些基础且常用的操作。这些几何变换并不改变图象的象素值，只是在图象平面上进行象素的重新排列。在一幅输入图象$[u，v]$中，灰度值仅在整数位置上有定义。然而，输出图象[x，y]的灰度值一般由处在非整数坐标上的$（u，v）$值来决定。这就需要插值算法来进行处理，常见的插值算法有最近邻插值、双线性插值和三次样条插值。

1.2 算法理论介绍与推荐

1.2.1 最近邻插值算法原理

  最近邻插值，是指将目标图像中的点，对应到源图像中后，找到$最相邻的整数点$，作为插值后的输出。

  如上图所示，目标图像中的某点投影到原图像中的位置为点P,此时易知，$f(P)=f(Q11)$.

一个例子：

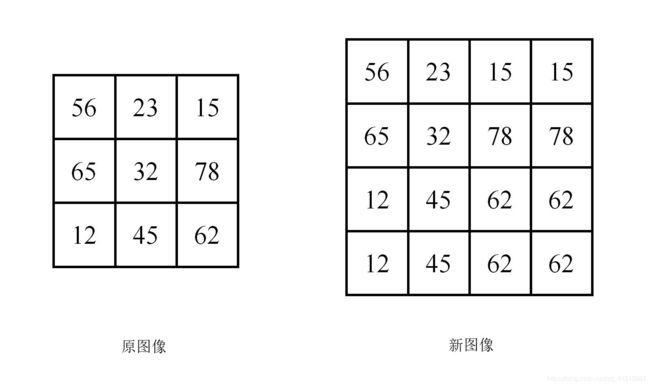
  如下图所示，将一幅3X3的图像放大到4X4，用$f(x,y)$表示目标图像，$h(x,y)$表示原图像，我们有如下公式：

$$\begin{array}{c}f(ds{t}_X,ds{t}_Y)=h(\frac{ds{t}_{X}sr{c}_{Width}}{ds{t}_{Width}},\frac{ds{t}_{Y}sr{c}_{Height}}{ds{t}_{Height}})\end{array}$$

$$\begin{array}{c}f(0,0)=h(0,0)\\ f(0,1)=h(0,0.75)=h(0,1)\\ f(0,2)=h(0,1.50)=h(0,2)\\ f(0,3)=h(0,2.25)=h(0,2)\\ ...\end{array}$$

$注意：小数部分遵循四舍五入！比如h(0,1.50)=h(0,2)（也可以采用直接舍掉小数位的方法）$

另外缩小也是相同的公式，由高等数学知识知：单调函数必有反函数。因为该函数为单调不减函数，所以推理可知最近邻法放大n倍再缩小为原来1/n还是原图，下面用代码验证一下：

import cv2
import numpy as np

arr = np.random.randint(255, size=(500, 500), dtype=np.uint8)

amplifier = cv2.resize(arr, dsize=None, fx=2, fy=2, interpolation = cv2.INTER_NEAREST)

minimise = cv2.resize(amplifier, dsize=None, fx=0.5, fy=0.5, interpolation = cv2.INTER_NEAREST)

print((minimise == arr).sum())

输出为250000，刚好为500*500，所以可以证明我们的推理

缺点：
用该方法作放大处理时，在图象中可能出现明显的块状效应

1.2.2 双线性插值

  在讲双线性插值之前先看以一下线性插值，线性插值多项式为：

$$f(x)=a_{1}x+a_0$$

$$y=y_0+\left(x-x_0\right)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{\left(x-x_0\right)y_1-\left(x-x_0\right)y_0}{x_1-x_0}$$

双线性插值

如图，已知$Q_{12}，Q_{22}，Q_{11}，Q_{21}$，但是要插值的点为$P$点，这就要用双线性插值了，首先在$x$轴方向上，对$R_1$和$R_2$两个点进行插值，这个很简单，然后根据$R_1$和$R_2$对$P$点进行插值，这就是所谓的双线性插值。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

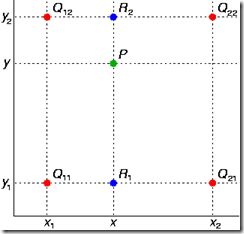
设$Q_{11}=(x_1,y_1)、Q_{12}=(x_1,y_2),Q_{21}=(x_2,y_1)以及Q_{22}=(x_2,y_2)$
首先在$x$方向进行线性插值，得到

$$f(R_1)\approx \frac{x-x_2}{x_1-x_2}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$$
$$f(R_2)\approx \frac{x-x_2}{x_1-x_2}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$$

然后在$y$方向进行线性插值，得到：

$$f(P)\approx \frac{y-y_2}{y_1-y_2}f(R_1)+\frac{y-y_1}{y_2-y_1}{R}_2$$

$将f(R_1)、f(R_2)带入上式得：$

$$f(P)\approx \frac{y-y_2}{y_1-y_2}\frac{x-x_2}{x_1-x_2}f(Q_{11})+\frac{y-y_2}{y_1-y_2}\frac{x-x_1}{x_2-x_1}f(Q_{21})+\frac{y-y_1}{y_2-y_1}\frac{x-x_2}{x_1-x_2}f(Q_{12})+\frac{y-y_1}{y_2-y_1}\frac{x-x_1}{x_2-x_1}f(Q_{22})$$

这就是双线性插值最后的结果，由于图像双线性插值只会用相邻的4个点，因此上述公式的分母都是1,图像双线性插值原理如下：

  令$f(x，y)$为两个变量的函数，其在单位正方形顶点的值已知。假设我们希望通过插值得到正方形内任意点的函数值。则可由双线性方程:
$$f(x,y)=ax+by+cxy+d$$

  来定义的一个双曲抛物面与四个已知点拟合。

  首先对上端的两个顶点进行线性插值得：

$$f(x,0)=f(0,0)+x[f(1,0)-f(0,0)]$$

  类似地，再对底端的两个顶点进行线性插值有：
$$f(x,1)=f(0,1)+x[f(1,1)-f(0,1)]$$

  最后，做垂直方向的线性插值，以确定：

$$f(x,y)=f(x,0)+y[f(x,1)-f(x,0)]$$

  整理得：

$$\begin{array}{l}f(x,y)=[f(1,0)-f(0,0)]x+[f(0,1)-f(0,0)]y\\ +[f(1,1)+f(0,0)-f(0,1)-f(1,0)]xy+f(0,0)\end{array}$$

用一开始的例子算一下：

$$\begin{array}{c}f(0,0)=h(0,0)=56\\ f(0,1)=h(0,0.75)=0.75\cdot (23-56)+56=31.25\\ f(0,2)=h(0,1.50)=0.5\cdot (15-23)+23=19\\ f(0,3)=h(0,2.25)=0.25\cdot ???\\ ...\end{array}$$

？？？可以看到，算到$f(0,3)$的时候不知道怎么带入公式了，并且我们用代码验证一下：

arr = np.array([[56, 23, 15], [65, 32, 78], [12, 45, 62]], dtype=np.uint8)
amplifier = cv2.resize(arr, dsize=None, fx=4/3, fy=4/3, interpolation = cv2.INTER_LINEAR)
print(amplifier)

输出：
[[56 35 20 15]
[62 41 38 54]
[45 40 50 72]
[12 33 51 62]]

可以看到，和我们手算的结果并不一样，这是为什么呢？？

看了这篇博客后才知道里面的原理

其实就是将源图像和目标图像几何中心的对齐 ，把一开始的公式：

$$f(ds{t}_X,ds{t}_Y)=h(\frac{ds{t}_{X}sr{c}_{Width}}{ds{t}_{Width}},\frac{ds{t}_{Y}sr{c}_{Height}}{ds{t}_{Height}})$$

改为：

$$f(ds{t}_X,ds{t}_Y)=h[\frac{(ds{t}_X+0.5)\ast sr{c}_{Width}}{ds{t}_{Width}}-0.5,\frac{(ds{t}_Y+0.5)\ast sr{c}_{Height}}{ds{t}_{Height}}-0.5]$$

另外，遇到边界时

参照这个评论处理，接下来我们重新手算一遍：

$$\begin{array}{c}f(0,0)=h(-0.125,-0.125)=h(0,0)=56\\ f(0,1)=h(-0.125,0.625)=h(0,0.625)=0.625\cdot (23-56)+56=35.375\approx 35\\ f(0,2)=h(-0.125,1.375)=h(0,1.375)=0.375\cdot (15-23)+23=20\\ f(0,3)=h(-0.125,2.125)=h(0,2)=15\\ f(1,0)=h(0.625,-0.125)=h(0.625,0)=0.625\cdot (65-56)+56=61.625\approx 62\\ f(1,1)=h(0.625,0.625)=h(0.625,0.625)\\ =0.625\cdot (65-56)+0.625\cdot (23-56)+0.625\cdot 0.625\cdot (56+32-65-23)+56\\ =41\\ ...\end{array}$$

可以看到和Opencv输出结果一样啦，hhhhhhh

另外，线性插值其实就是拉格朗日插值有两个取值点的情况
可以参考这篇文章理解一下：
https://www.zhihu.com/question/58333118

1.2.3 三次样条插值

为什么会有三次样条插值呢？
之前数值分析课做过实验：

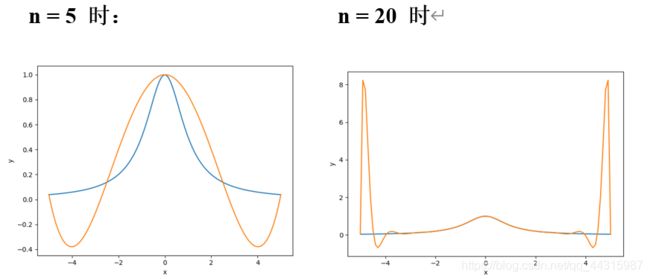
当n=5和n=20时，拉格朗日插值逼近（蓝色为原函数，橙色为拉格朗日插值）：

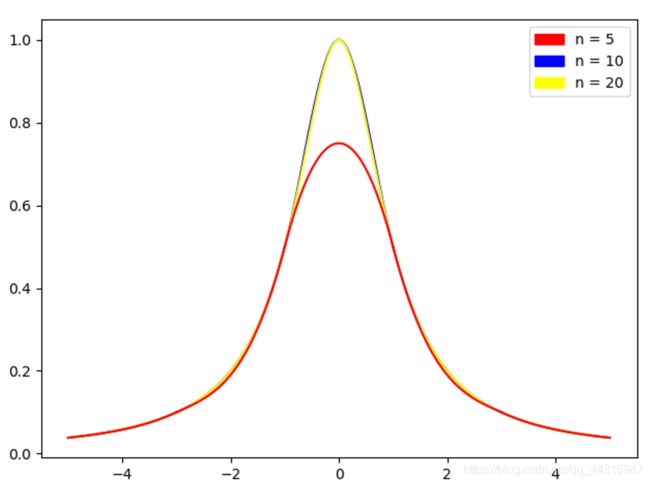
可以明显看出，随着n增大，拉格朗日插值会出现振荡现象，反观三弯角法（三次样条的一种）：

$可以看到n越大逼近效果越好$，但是缺点就是算的太慢

三次样条插值原理
  给定$n+1$个点，$a=x_0<x_1<...<x_n=b$，以及他们的函数值$f(x_i),i=0,1,2,...n$，在每个区间$[x_i,x_{i+1}]$上，确定一个三次多项式：
$$S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i{)}^2+d_i(x-x_i{)}^3，i=0,1,...n-1$$
  每个三次多项式中有四个未知参数，有$n$个区间，$n$个多项式，共$4n$个未知参数。我们知道“$n$个未知数需要$n$个已知条件确定唯一解”，所以要确定这$4n$个未知参数，共需要$4n$个已知条件。

  每个三次多项式满足如下条件：

• $S_i$二阶可导，且$S_i$，$S_i^{{}^{\prime }}$，$S_i^{{}^{\prime \prime }}$在区间$[a,b]$内连续
• $S_i(x_i)=y_i$，$S_i(x_{i+1})=y_{i+1}$，$i=0,1,...n-1$（共$n+1$个条件）
• $S_i(x_{i+1})=S_{i+1}(x_{i+1})$，$i=0,1,...n-2$（共$n-1$个条件）
• $S_i^{{}^{\prime }}(x_{i+1})=S_{i+1}^{{}^{\prime }}(x_{i+1})$，$i=0,1,...n-2$（共$n-1$个条件）
• $S_i^{{}^{\prime \prime }}(x_{i+1})=S_{i+1}^{{}^{\prime \prime }}(x_{i+1})$，$i=0,1,...n-2$（共$n-1$个条件）

  以上共$4n-2$个条件，还差2个条件，由如下三种边界条件确定：

• 给定端点处一阶导数值：$S_0^{{}^{\prime }}(x_0)=y_0^{{}^{\prime }}，S_{n-1}^{{}^{\prime }}(x_n)=y_n^{{}^{\prime }}$，称为固定边界条件

• 给定端点处二阶导数值：$S_0^{{}^{\prime \prime }}(x_0)=y_0^{{}^{\prime \prime }}，S_{n-1}^{{}^{\prime \prime }}(x_n)=y_n^{{}^{\prime \prime }}$，特别地，$y_0^{{}^{\prime \prime }}=y_n^{{}^{\prime \prime }}=0$，称为自然边界条件

• 周期性条件：$S_0(x_0-0)=S_{n-1}(x_n+0)$，$S_0^{{}^{\prime }}(x_0-0)=S_{n-1}^{{}^{\prime }}(x_n+0)$，
        $S_0^{{}^{\prime \prime }}(x_0-0)=S_{n-1}^{{}^{\prime \prime }}(x_n+0)$

  $4n$个条件有了，就可以确定每个区间上的三次多项式。

  对于每个区间内的点，就可以用$S_i(x)$得到插值结果。三次样条插值具有良好的收敛性，稳定性和光滑性，优点明显，是非常重要的插值工具。

  这里主要了解三次样条插值的作用，具体的推导过程比较繁琐，想了解的可以查阅资料。

流程图如下：

三次样条图像插值原理https://www.sohu.com/a/323023965_468740：

该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为：

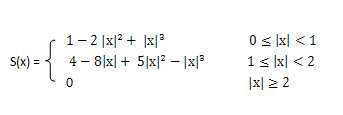
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到，如下图：

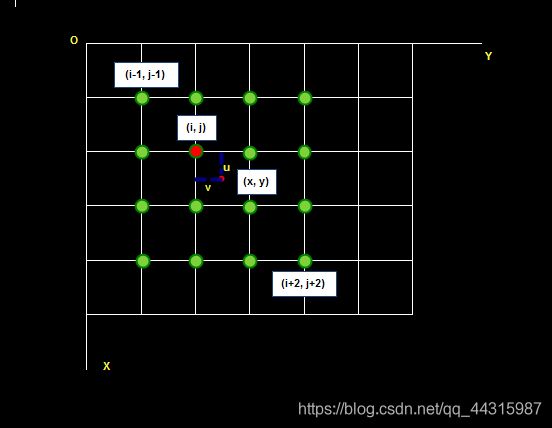
待求像素的灰度计算式如下：

$$f(x,y)=f(i+u,j+v)=ABC$$

其中:

1.2.4 映射方法

$假设变换前图像为I(x,y)，变换后图像为I^{\prime }(x^{\prime },y^{\prime })，则变换前后的图像之间存在下列关系：$

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}f(x,y)\\ g(x,y)\end{array}\right)(1)$$

$$I(x,y)=I^{\prime }(x^{\prime },y^{\prime })=I^{\prime }(f(x,y),g(x,y))$$

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{f}^{-1}(x^{\prime },y^{\prime })\\ g^{-1}(x^{\prime },y^{\prime })\end{array}\right)(2)$$

$$I^{\prime }(x^{\prime },y^{\prime })=I^{\prime }(x^{\prime },y^{\prime })=I^{\prime }(f^{-1}(x^{\prime },y^{\prime }),g^{-1}(x^{\prime },y^{\prime }))$$

向前映射法

  可以将几何运算想象成一次一个象素地转移到输出图象中。如果一个输入象素被映射到四个输出象素之间的位置，则其灰度值就按插值算法在4个输出象素之间进行分配。称为向前映射法，或象素移交影射。

注：从原图象坐标计算出目标图象坐标镜像、平移变换使用这种计算方法

由公式(1)我们已知原图像到目标图像的坐标变换$(f(x,y),g(x,y))$，因此我们可以知道原图像的一点在变换后在目标图像的位置，我们称为向前映射。

向后映射法

  向后映射法（或象素填充算法）是输出象素一次一个地映射回到输入象素中，以便确定其灰度级。如果一个输出象素被映射到4个输入象素之间，则其灰度值插值决定，向后空间变换是向前变换的逆。

注：从结果图象的坐标计算原图象的坐标

公式(2)中我们知道目标图像的一点(x’,y’)在变换前在原图像上的位置$(f-1(x\prime ,y\prime ),g-1(x\prime ,y\prime ))$，我们称为向后映射。

总结

• 旋转、拉伸、放缩可以使用
• 解决了漏点的问题，出现了马赛克

向后映射比较直观，计算量也小，我们经常使用的图像变换都是采用向后映射的方法来处理。但向后映射需要知道变换的反函数。但在有些变换比较复杂的场合，这个反变换是很难得到的。此时就需要采用前向映射的方法进行变换了。

1.3 基于OpenCV的实现

1.3.1 C++ 伸缩操作

函数原型：

void cv::resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR )

src:输入图像
dst:输出图像
dsize:输出图像尺寸
fx、fy:x,y方向上的缩放因子
INTER_LINEAR：插值方法，总共五种
    1. INTER_NEAREST - 最近邻插值法
    2. INTER_LINEAR - 双线性插值法（默认）
    3. INTER_AREA - 基于局部像素的重采样(resampling using pixel area relation)。对于图像抽取(image decimation)来说，这可能是一个更好的方法。但如果是放大图像时，它和最近邻法的效果类似。
    4. INTER_CUBIC - 基于4x4像素邻域的3次插值法
    5. INTER_LANCZOS4 - 基于8x8像素邻域的Lanczos插值

代码实践：

#include 
#include 

using namespace cv;
using namespace std;

int main(int argc, char* argv[])
{
	Mat img = imread("D:/image/yuner.jpg");
	if (img.empty())
	{
		cout << "无法读取图像" << endl;
		return 0;
	}

	int height = img.rows;
	int width = img.cols;
	// 缩小图像，比例为(0.2, 0.2)
	Size dsize = Size(round(0.2 * width), round(0.2 * height));
	Mat shrink;
    //使用双线性插值
	resize(img, shrink, dsize, 0, 0, INTER_LINEAR);

	// 在缩小图像的基础上，放大图像，比例为(1.5, 1.5)
	float fx = 1.5;
	float fy = 1.5;
	Mat enlarge1, enlarge2;
	resize(shrink, enlarge1, Size(), fx, fy, INTER_NEAREST);
	resize(shrink, enlarge2, Size(), fx, fy, INTER_LINEAR);

	// 显示
	imshow("src", img);
	imshow("shrink", shrink);
	imshow("INTER_NEAREST", enlarge1);
	imshow("INTER_LINEAR", enlarge2);
	waitKey(0);
    return 0;
}

原图

0.2倍缩小，双线性插值

1.5倍放大，最近邻插值

1.5倍放大，双线性插值

仔细观察可以看出，最邻近法有块状效应，而双线性插值法效果较好

1.3.2 Python

函数原型：

cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])

参数：

参数	描述
src	【必需】原图像
dsize	【必需】输出图像所需大小
fx	【可选】沿水平轴的比例因子
fy	【可选】沿垂直轴的比例因子
interpolation	【可选】插值方式

插值方式：

cv.INTER_NEAREST	最近邻插值
cv.INTER_LINEAR	双线性插值
cv.INTER_CUBIC	基于4x4像素邻域的3次插值法
cv.INTER_AREA	基于局部像素的重采样

通常，缩小使用cv.INTER_AREA，放缩使用cv.INTER_CUBIC(较慢)和cv.INTER_LINEAR(较快效果也不错)。默认情况下，所有的放缩都使用cv.INTER_LINEAR。

代码实践：

下面介绍一些python opencv的基本函数的参数

1.imread(filename, flags=None)

flags	解释
IMREAD_UNCHANGED	指定用图片的原来格式打开，即以不改变图片的方式打开，图片是彩色就是彩色，图片是灰度图像就是灰度图像
IMREAD_GRAYSCALE	指定用灰度图像的方式打开图片，即将原始图像转化为灰度图像再打开
IMREAD_COLOR	指定用彩色图像打开图片

import cv2
 
if __name__ == "__main__":
    img = cv2.imread('D:/image/yuner.jpg', cv2.IMREAD_UNCHANGED)
    
    print('Original Dimensions : ',img.shape)
    
    scale_percent = 30       # percent of original size
    width = int(img.shape[1] * scale_percent / 100)
    height = int(img.shape[0] * scale_percent / 100)
    dim = (width, height)
    # resize image
    resized = cv2.resize(img, dim, interpolation = cv2.INTER_LINEAR)

    fx = 1.5
    fy = 1.5

    resized1 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_NEAREST)
    
    resized2 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_LINEAR)
    print('Resized Dimensions : ',resized.shape)
    
    cv2.imshow("Resized image", resized)
    cv2.imshow("INTER_NEAREST image", resized1)
    cv2.imshow("INTER_LINEAR image", resized2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

0.3倍缩小，双线性插值

1.5倍放大，最近邻插值

1.5倍放大，双线性插值

• 推荐书籍：学习OpenCV中文版
• 推荐博客：https://blog.csdn.net/hongbin_xu/category_6936122.html

1.6 总结

  插值算法是很多几何变换的基础和前置条件，对插值算法细节的掌握有助于对其他算法的理解，为自己的学习打下坚实的基础。

关于Datawhale：

Datawhale是一个专注于数据科学与AI领域的开源组织，汇集了众多领域院校和知名企业的优秀学习者，聚合了一群有开源精神和探索精神的团队成员。Datawhale以“for the learner，和学习者一起成长”为愿景，鼓励真实地展现自我、开放包容、互信互助、敢于试错和勇于担当。同时Datawhale 用开源的理念去探索开源内容、开源学习和开源方案，赋能人才培养，助力人才成长，建立起人与人，人与知识，人与企业和人与未来的联结。