深度学习入门基于python的的理论与实现（学习笔记）.第七章 卷积神经网络（第二部分）

• 池化层：
  池化是缩小高、长方向上的空间的运算。
  
  一般来说，池化的窗口大小会和步幅设定成相同的值。

• 池化层的特征
  1. 没有要学习的参数
  2.通道数不发生变化
  
  对微小的位置变化具有鲁棒性（健壮）。输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对输入数据的微小偏差具有鲁棒性。
  因此，池化层可以降低特征图的参数量，提升计算速度，增加感受野，是一种降采样的操作。可是模型更关注全局特征而非局部出现的位置，可提升容错能力，一定程度上防止过拟合。

• 卷积层和池化层的实现：
  为了实现卷积层和池化层，我们首先引入一个“函数” im2col。im2col是一个函数，将输入数据展开以适合滤波器（权重）。如下图所示，对3维的输入数据应用im2col后，数据转换为2维矩阵（正确地讲，是把包含批数量的4维数据转换成了2维数据）。
  
  im2col对于输入数据，将应用滤波器的区域（3 维方块）横向展开为1 列。im2col会在所有应用滤波器的地方进行这个展开处理。
  
  在上图中，为了便于观察，将步幅设置得很大，以使滤波器的应用区域不重叠。而在实际的卷积运算中，滤波器的应用区域几乎都是重叠的。在滤波器的应用区域重叠的情况下，使用im2col展开后，展开后的元素个数会多于原方块的元素个数。因此，使用im2col的实现存在比普通的实现消耗更多内存的缺点。但是，汇总成一个大的矩阵进行计算，对计算机的计算颇有益处。
  
  可知变换为：
  
  可以看出，在输出数据(2维)中，矩阵的一列即为输入特征图经过一个滤波器之后的结果。
  代码实现：
  前向运算im2col：

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h) // stride + 1 # 向下取整
    out_w = (W + 2 * pad - filter_w) // stride + 1

    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, out_h, out_w, filter_h, filter_w))

    # x_min 和 y_min 用于界定一个滤波器作用的方块区域
    for y in range(out_h):
        y_min = y * stride
        for x in range(out_w):
            x_min = x * stride
            col[:, :, y, x, :, :] = img[:, :, y_min:y_min+filter_h, x_min:x_min+filter_w]
    col = col.transpose(0, 2, 3, 1, 4, 5).reshape(N*out_h*out_w, -1)

    return col

当然，在反向传播的时候还需要im2col函数的逆处理col2im函数。由于在卷积运算的过程中，滤波器的作用区域可能是重合的，因此img中的一个元素可能会多次出现在col中，根据链式法则，img中元素的偏导即为col中所有该元素所在位置的偏导之和。
反向传播 col2im：

def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_shape # padding之前的图像大小
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1

    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 1, 2, 4, 5)

    img = np.zeros((N, C, H + 2 * pad, W + 2 * pad))
    for y in range(out_h):
        y_min = y * stride
        for x in range(out_w):
            x_min = x * stride
            # 要注意这里是 += 而非 = ，原因就是上面的那段话
            img[:, :, y_min:y_min+filter_h, x_min:x_min+filter_w] += col[:, :, y, x, :, :]

    return img[:, :, pad:H+pad, pad:W+pad]

• 卷积层实现：

class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad

        self.x = None
        self.col = None
        self.col_W = None

        self.db = None
        self.dW = None

    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = (H + 2 * self.pad - FH) // self.stride + 1
        out_w = (W + 2 * self.pad - FW) // self.stride + 1        

        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN, -1).T

        out = (np.dot(col, col_W) + self.b).reshape(N, out_h, out_w, FN).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
        
        self.db = dout.sum(axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.T.reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

• Max池化层的实现：
  池化层的实现和卷积层相同，都使用im2col展开输入数据。不过，池化的情况下，在通道方向上是独立的，这一点和卷积层不同。池化的应用区域应该按通道单独展开。
  
  
  
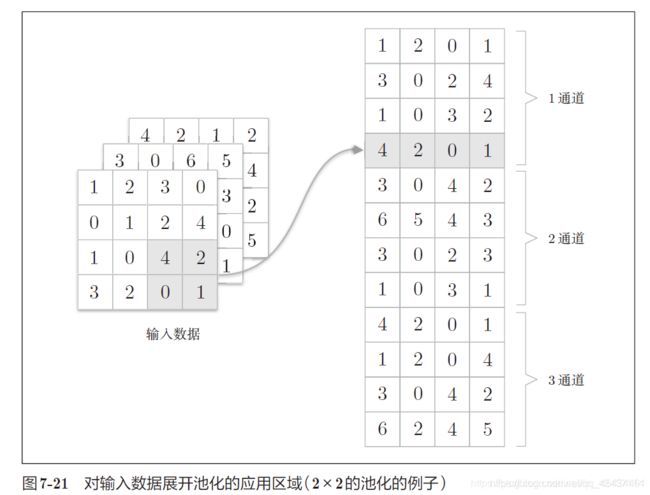
  反向传播类似于Relu的反向传播，只要在正向传播时保存好各个滤波器中最大值的索引位置即可。
  代码实现：

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad

        self.mask = None

    def forward(self, x):
        N, C, H, W = x.shape

        out_h = (H + 2 * self.pad - self.pool_h) // self.stride + 1
        out_w = (W + 2 * self.pad - self.pool_w) // self.stride + 1

        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(N, out_h * out_w, C, self.pool_h * self.pool_w).transpose(0, 2, 1, 3).reshape(N * C * out_h * out_w, self.pool_h * self.pool_w)

        mask = np.argmax(col, axis=1)
        out = col[np.arange(mask.size), mask]
        out = out.reshape(N, C, out_h, out_w)

        self.mask = mask
        self.input_shape = x.shape

        return out

    def backward(self, dout):
        N, C, H, W = self.input_shape

        out_h = (H + 2 * self.pad - self.pool_h) // self.stride + 1
        out_w = (W + 2 * self.pad - self.pool_w) // self.stride + 1

        dout = dout.reshape(N * C * out_h * out_w)
        dcol = np.zeros((N * C * out_h * out_w, self.pool_h * self.pool_w))
        dcol[np.arange(self.mask.size), self.mask] = dout

        dcol = dcol.reshape(N, C, out_h * out_w, self.pool_h * self.pool_w).transpose(0, 2, 1, 3).reshape(N * out_h * out_w, C * self.pool_h * self.pool_w)
        dx = col2im(dcol, self.input_shape, self.pool_h, self.pool_w, self.stride, self.pad)

        return dx