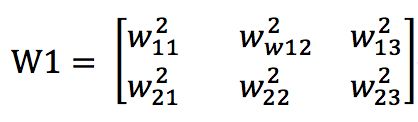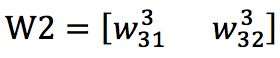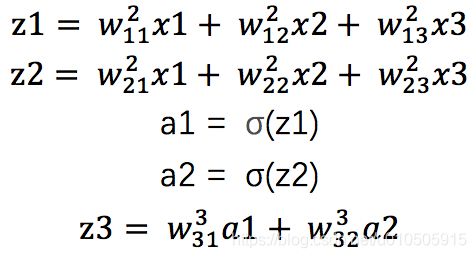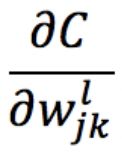神经网络参数初始化
神经网络的参数有权重(weights)W和偏置(bias)b。训练神经网络,需要先给网络参数W和b赋初始值,然后经过前向传播和后向传播,迭代更新W和b。这些参数的初始值对于神经网络收敛的速度及神经网络的准确率有很大影响。那么,应该怎么初始化这些参数呢?
不能采用的方法
全0初始化
这部分会从神经网络前向传播及后向传播的角度进行分析,不熟悉前向传播和后向传播的朋友,可以参考我的另一篇博客:神经网络的前向传播和反向传播
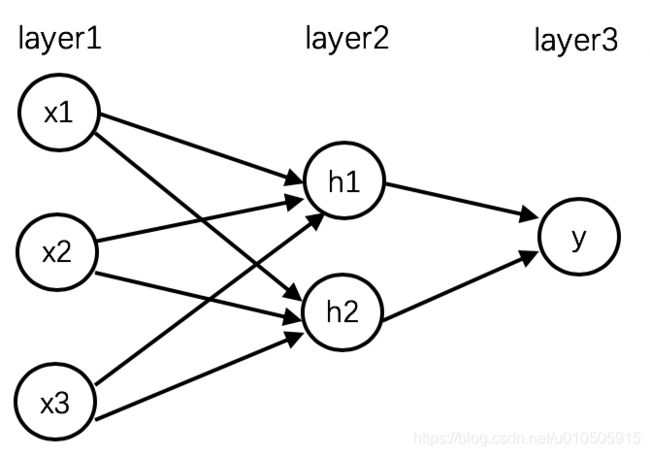
假设神经网络有一个输入层、隐层、输出层,如下:
图1:神经网络结构图
以上神经网络中,layer1的输入为x1, x2, x3,layer2的值为z1, z2,经激活函数转换后输出a1, a2。layer3的值为z3。
layer1到layer2的权重矩阵为:
layer2到layer3的权重矩阵为:
则前向传播为(忽略bias):
根据《神经网络的前向传播和反向传播》中所述反向传播算法:
代码函数对权重的改变率(及导数)为:
![]() (BP4)
(BP4)
![]() (BP2)
(BP2)
若bias为0,由于:
![]() (BP3)
(BP3)
则bias也无法更新。
全相同常数初始化
不能全0初始化,那能不能采用相同的常数初始化呢?这样导数就不是0了。
我们还是以图1所示神经网络结构进行说明。如果w初始值一样,则隐层中的两个节点,其输入值、输出值完全一样,那么反向传播的时候,两个节点的梯度也完全相同。无论进行多少轮训练,这两个节点完全等价。无论这层有多少个节点,都相当于只有一个节点,其他节点的参数都是冗余的。
所以,每层的参数都不能是相同的常数。第一层全是a,第二层全是b这种也不可以。即,网络不能是对称的。
可以采用的方法
不能使用相同的常数,也就意味着对参数的初始化,需要随机性。那有哪些随机方法呢?下面逐一说明。
注:本节以coursera上Planar data classification为例进行说明,部分代码参考了 https://www.pianshen.com/article/3355323669/
随机初始化
先补一个全0初始值的cost曲线:
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
W1 = np.zeros((n_h, n_x))
b1 = np.zeros((n_h, 1))
W2 = np.zeros((n_y, n_h))
b2 = np.zeros((n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
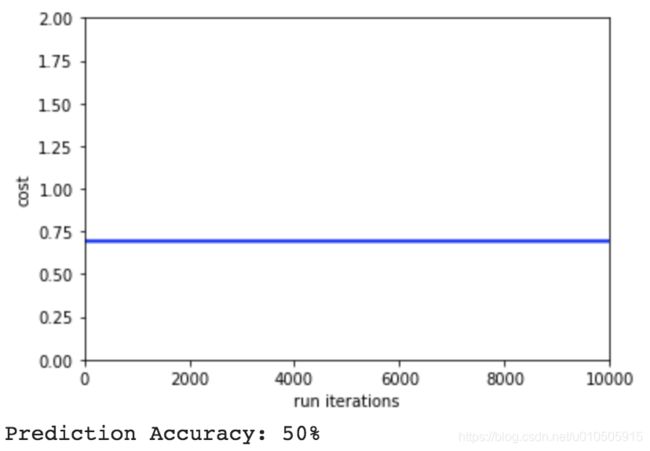
return parameterscost曲线:
由于参数w不变,迭代时cost不会改变。
下面看看随机初始值:
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
W1 = np.random.randn(n_h, n_x)
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)
b2 = np.zeros((n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parametersrandom.rand()是在0~1之间随机,random.randn()是标准正态分布中随机,有正有负。
b不用随机初始化,因为w随机之后,已经打破对称,b就一个常数,无所谓了。
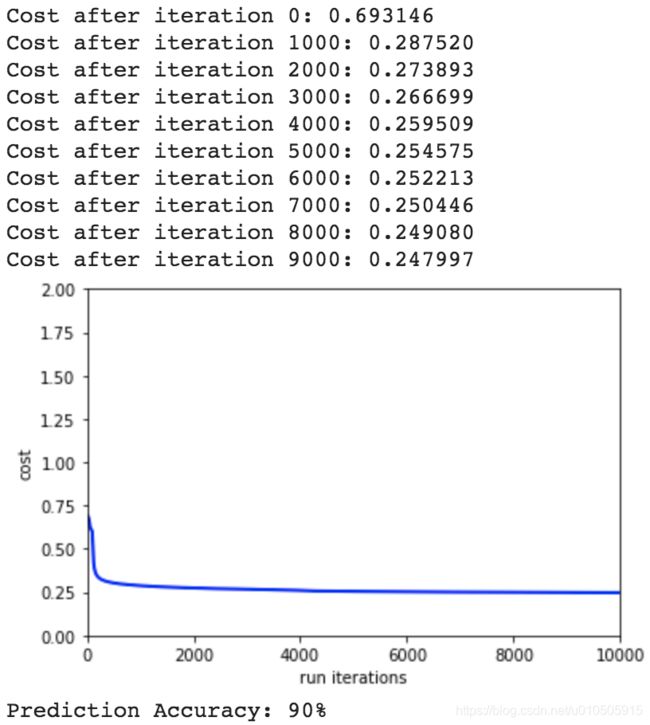
效果:
随机初始化-适当缩小w
随机初始化w之后,再乘一个比较小的数,比如0.01
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
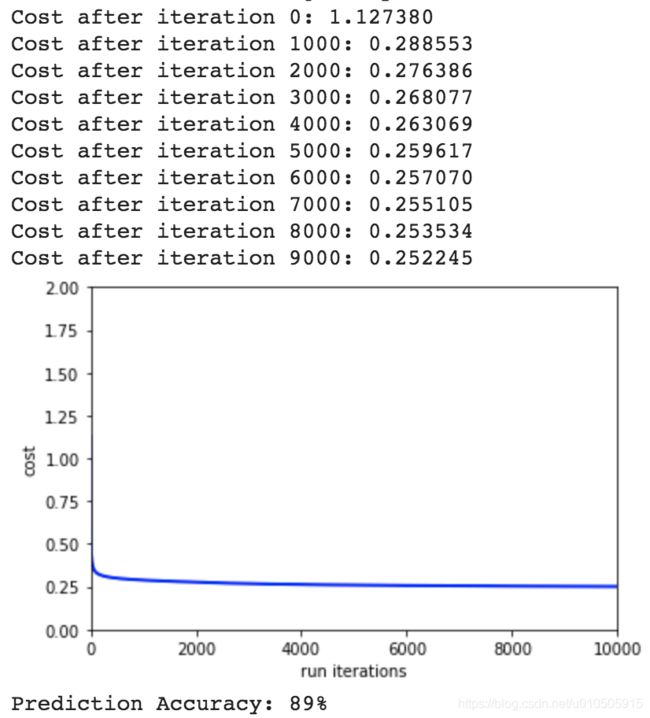
return parameters运行效果:
效果稍好一些。
随机初始化-极小的w
随机初始化w之后,把w再缩小一些,比如乘以0.001,效果:
此时cost反而变大。说明随机初始化w之后,需要适当的调整w的值。
其实,如果w的初始值太小,在网络层数比较多时,可能会出现问题,最后参数全部为0。首先,在前向传播时,输出z = σ(wx + b)因为w很小,所以输出z很小。同时,反向传播过程中,梯度的变化也很小,参数的改变也很小。在不断的正向传播乘很小的数,反向传播又几乎不变的情况下,最后w会越来越小,趋近于0,出现梯度弥散现象。
随机初始化-极大的w
随机初始化w之后,把w再扩大10倍:
def initialize_parameters(n_x, n_h, n_y):
...
W1 = np.random.randn(n_h, n_x) * 100
W2 = np.random.randn(n_y, n_h) * 100
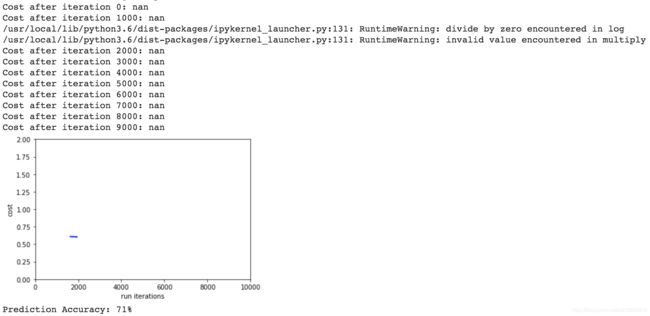
...效果:
效果比较差。
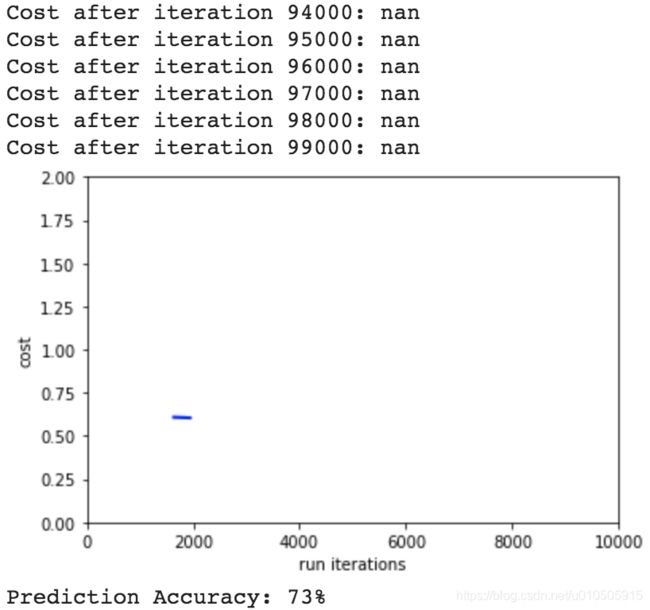
把迭代次数增加10倍,从预测准确率看,效果稍微好一点,但还是比较差:
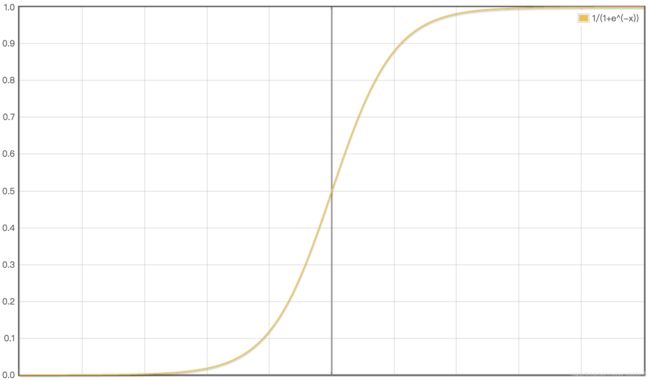
本次实验,隐层的激活函数为sigmoid/tanh,我们先看看sigmoid函数:
sigmoid函数中间的斜率大,两边的斜率小,趋于零。所以当我们把随机值乘以100了之后,初始值会往两边跑,由于两边梯度趋于0,梯度下降显著变慢,可能迭代很多次,才下降一点点。
这就是问题的症结。
这种是典型的学习慢,在相同的迭代次数下,使用极大的初始w的模型,学习较慢,效果就较差。
生成随机值之后,适当调整随机值的大小作为初始的w,是能够提高模型准确率的。每次一个个的试成本比较高,那有没有通用的方法或理论指导呢?
有,对使用不同激活函数的网络层,有不同的指导方法。我们接着看:
标准初始化
Xavier初始化
He初始化
Xavier初始化和He初始化,比较复杂,决定单写个博客详细介绍
附录:
Planar data classification部分代码:
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
#planar_utils
def plot_decision_boundary(model, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(x)
"""
s = 1 / (1 + np.exp(-x))
return s
def load_planar_dataset(rseed):
np.random.seed(rseed)
m = 400 # number of examples
N = int(m / 2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m, D)) # data matrix where each row is a single example
Y = np.zeros((m, 1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2):
ix = range(N * j, N * (j + 1))
t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2 # theta
r = a * np.sin(4 * t) + np.random.randn(N) * 0.2 # radius
X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
#main program
np.random.seed(1) # set a seed so that the results are consistent
X, Y = load_planar_dataset(1)
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1] # training set size
print ('The shape of X is: ' + str(shape_X)) #每个样本为2维,即输入层为2个单元,总共有400个样本
print ('The shape of Y is: ' + str(shape_Y)) #总共有400个标签,400个样本
print ('I have m = %d training examples!' % (m))
# 定义每个层的单元数
def layer_sizes(X, Y):
n_x = X.shape[0] # size of input layer
n_h = 4 #hide_layer神经元的个数
n_y = Y.shape[0] # size of output layer
return (n_x, n_h, n_y)
#初始化权重
#神经网络中权重不能初始化为0,针对逻辑回归,可为0
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
W1 = np.random.randn(n_h, n_x)
#W1 = np.zeros((n_h, n_x))
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)
#W2 = np.zeros((n_y, n_h))
b2 = np.zeros((n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def forward_propagation(X, parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
assert (A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache #A2为最终的输出,cache为每一层的缓存,即每层的z值,激活值
def compute_cost(A2, Y, parameters):
m = Y.shape[1] # number of example
logprobs = Y * np.log(A2) + (1 - Y) * np.log(1 - A2) #A2为输出值
cost = -1./ m * np.sum(logprobs) #一定要注意,此处为-1. 浮点数 否则为计算出错
cost = np.squeeze(cost) # makes sure cost is the dimension we expect.
assert (isinstance(cost, float)) #isinstance(object, classinfo) 判断cost的数据类型 返回True or false
return cost
def backward_propagation(parameters, cache, X, Y):
m = X.shape[1] #数据的个数
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1./ m * np.sum(dZ2, axis=1, keepdims=True) #此处的1要全部改为1. 浮点数运算
dZ1 = np.dot(W2.T, dZ2) * (1. - np.power(A1, 2)) #np.power 计算A1的平方 此处用的激活函数为tanh(z),导数为1-a1的平方
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
def update_parameters(parameters, grads, learning_rate=1.2):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def plot_cost(cost_list):
plt.figure()
plt.plot(cost_list[:, 1], cost_list[:, 0],
color='blue', linewidth=2)
plt.xlabel('run iterations')
plt.ylabel('cost')
#plt.title('cost-iteration')
plt.ylim([0.0, 2.0])
plt.xlim([0, 10000])
plt.show()
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 初始化权重, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
cost_iter_list = []
for i in range(0, num_iterations):
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
A2, cache = forward_propagation(X, parameters) #A2为前向传播的最终输出,cache为每一层的z值和激活值
# Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
cost = compute_cost(A2, Y, parameters)
cost_iter_list.append([cost, i])
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
grads = backward_propagation(parameters, cache, X, Y) #梯度,为每一层的dw dz
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
parameters = update_parameters(parameters, grads) #对每一层的权重进行更新
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
plot_cost(np.array(cost_iter_list))
return parameters
def predict(parameters, X):
# Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2)
return predictions
# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# Plot the decision boundary
#plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
#plt.title("Decision Boundary for hidden layer size " + str(4))
# Print accuracy
X_test, Y_test = load_planar_dataset(2)
predictions = predict(parameters, X_test)
print ('Prediction Accuracy: %d' % float((np.dot(Y_test,predictions.T) + np.dot(1-Y_test,1-predictions.T))/float(Y_test.size)*100) + '%')