数据挖掘笔记(5)-关联规则算法Apriori
1、关联规则概念
如果去超市买东西,我们会发现购买了牛奶的客户很可能会去购买面包,那么“牛奶=>面包”就称之为关联规则,其中牛奶是前项,面包是后项,它们都是项集(单项集)。
2、关联规则算法Apriori
Apriori是最常用也是最经典的挖掘频繁项集的算法,其核心思想是通过连接产生候选项及其支持度,然后通过剪枝生成频繁项集。
(1)项集
项集是项的集合,包含k个项的就是k项集,如{牛奶,面包}就是一个2项集。
(2)项集的支持度计数
项集A的支持度计数就是事务集中包含项集A的事务的个数,用Support_count(A)表示。事务集包含的所有事务个数用Total_count(事务集)表示。
(3)支持度和置信度
A、B为项集,A=>B为关联规则。
项集的支持度:

关联规则的支持度:
(相当于Support(A U B),A U B也是一个项集。也就是说关联规则的支持度等于由关联规则的前项和后项组成的项集的支持度)

关联规则的置信度:

(4)最小支持度和最小置信度
最小支持度是用户或专家定义的衡量支持度的一个阈值,表示项集的最低重要性。
最小置信度是用户或专家定义的衡量置信度的一个阈值,表示关联规则的最低可靠性。
满足最小支持度的项集称作频繁项集。
同时满足最小支持度和最小置信度的关联规则称作强规则。
(5)算法流程
餐厅的订单信息如下:
菜品{18491,8842,8693,7794,8705}分别用{a, b, c, d, e}表示

过程一:找最大的频繁k项集集合
(假定最小支持度为0.2,最小置信度为0.5)
- 扫面所有事务,事务中发生的每一项都是候选1项集的集合C1中的成员,C1={{a},{b},{c},{d},{e}}
- 计算C1中的每一个候选1项集的支持度,保留大于或者等于最小支持度的项集得到频繁1项集集合L1={{a},{b},{c},{d},{e}}。
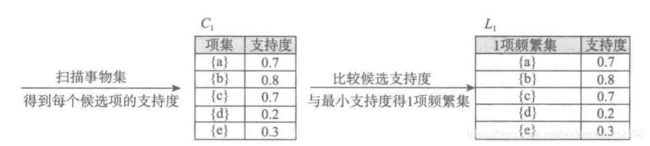
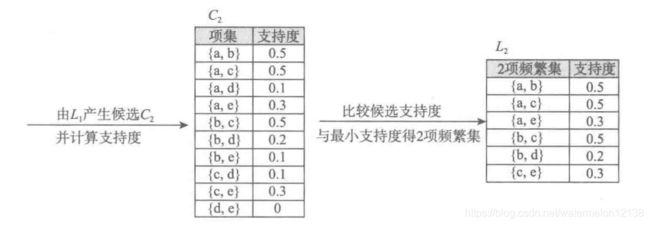
- 连接L1和L1得到候选2项集集合C2={{a, b},{a,c},{a,d},{a,e},{b,c},{b,d},{b,e},{c,d},{c,e},{d,e}},接下来是剪枝,由于C2的每一项的子集都是频繁项集,所以C2不用剔除任何项。
- 计算C2中的每一个候选2项集的支持度,保留大于或者等于最小支持度的项集得到频繁2项集集合L2={{a, b},{a,c},{a,e},{b,c},{b,d},{c,e}}。
- 连接L2和L1得到候选3项集集合C3={{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,e,d},{b,c,d},{b,c,e},{b,d,e},{c,e,d}}。接下来进行剪枝处理,对于C3中的每一项,如果它的子集不是频繁项集,则剔除该项。因为{a,d},{b,e},{c,d},{d,e}没有在L2中,所以它们不是频繁项集,所以C3中应剔除{a,b,d},{a,b,e},{a,c,d},{a,e,d},{b,c,d},{b,c,e},{b,d,e},{c,e,d},最后C3中只剩{a,b,c},{a,c,e}。
- 计算C3中的每一个候选3项集的支持度,保留大于或者等于最小支持度的项集得到频繁3项集集合L3={{a,b,c},{a,c,e}}。
- L3与L1连接得候选4项集集合C4={{a, b, c, d},{a, b, c,e},{a,c,e,d}},因为{b,c,d},{b,c,e},{c,e,d}不在L3中,所以它们不是频繁项集,所以C4剪枝后为空集。即最终得到最大的3项频繁集集合L3={{a,b,c},{a,c,e}}。
由上述过程可知L1、L2、L3都是频繁项集的集合,而L3是最大的3项频繁集集合。
简化求候选k项集集合:对于编程来说,求候选k项集集合的时候可以直接通过频繁k-1项集集合L(k-1)得到。比如在求候选3项集集合C3时,我们通过频繁2项集集合L2直接来求,因为L2={{a, b},{a,c},{a,e},{b,c},{b,d},{c,e}},对于L2中的任意两项,如果它们满足只有最后的一位不同,而前面的所有位都相同这个条件,那就将这两项合并,所以由L2可以得到{a,b,c},{a,b,e},{a,c,e},{b,c,d},这求出了C3,C3={{a,b,c},{a,b,e},{a,c,e},{b,c,d}}。相比步骤5中求出的C3,这种简化剪枝的方法相当方便。
剪枝等价于最小支持度过滤:对于候选k项集集合Ck中的每一项,如果它的子集不是频繁项集,那该项的支持度一定低于最小支持度。可以通过最小支持度筛选Ck直接得到Lk,避免繁琐的剪枝过程。
过程二:由L2级别以上(包括L2级别)的频繁项集集合产生关联规则并根据最小置信度筛选可靠的关联规则
由过程一可以得到频繁项集集合L1、L2和L3,接下来过程二就由L2和L3中的频繁项集产生关联规则。
对于L2={{a, b},{a,c},{a,e},{b,c},{b,d},{c,e}},由频繁项集{a,b}可产生关联规则{a=>b},{b=>a},由频繁项集{a,c}可产生关联规则{a=>c},{c=>a},以此类推,L2中的频繁项集总共产生的关联规则有{a=>b},{b=>a},{a=>c},{c=>a},{a=>e},{e=>a},{b=>c},{c=>b},{b=>d},{d=>b},{c=>e},{e=>c}。
对于L3={{a,b,c},{a,c,e}},由频繁项集{a,b,c}产生的关联规则有{a,b=>c},{c=>a,b},{a,c=>b},{b=>a,c},{b,c=>a},{a=>b,c},由频繁项集{a,c,e}产生的关联规则有{a,c=>e},{e=>a,c},{a,e=>c},{c=>a,e},{c,e=>a},{a=>c,e},所以L3中的频繁项集总共产生的关联规则有{a,b=>c},{c=>a,b},{a,c=>b},{b=>a,c},{b,c=>a},{a=>b,c},{a,c=>e},{e=>a,c},{a,e=>c},{c=>a,e},{c,e=>a},{a=>c,e}。
最后计算过程二得到的所有关联规则的置信度,并根据最小置信度筛选可靠的关联规则。
例子:(该例子为算法流程中的案例)
下图中有10个事务,a、b、c、d、e为总结出的5个1项集,计算可能的关联规则及其支持度和置信度?
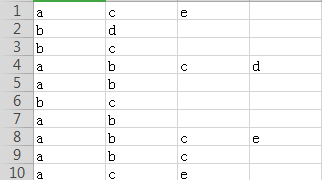
(1)apriori模块(apriori .py)
# -*- coding: utf-8 -*-
from __future__ import print_function
import pandas as pd
def connect_string(x, ms):
"""
简化方法求候选k项集集合
如 x = ['a', 'c', 'e', 'b']
连接后得到 r = [['a', 'c'], ['a', 'e'], ['a', 'b'], ['a', 'd'], ['c', 'e'], ['b', 'c'], ['c', 'd'], ['b', 'e'], ['d', 'e'], ['b', 'd']]
"""
print('x1: \n', x)
x = list(map(lambda i: sorted(i.split(ms)), x))
print('x2: \n', x)
l = len(x[0])
# print('x[0][:l-1]: \n', x[0][:l-1])
# print('l: \n', l)
r = []
# 比如x= [['a', 'c'], ['a', 'e'], ['a', 'b'], ['c', 'e'], ['b', 'c'], ['b', 'd']]第一个for循环表示遍历列表中的每一个列表
# 第二个for循环表示遍历从当前位置j处的列表一直到最后一个列表,j=0,1,2,...len(x)-1
# 如i=0,j=0时,判断x中的第一个列表和第一个列表除了最后一项以外是否都相等并且最后一项不相等,显然最后一项相等所以不成立
# 如i=0, j=1,判断x中的第一个列表和第二个列表除了最后一项以外是否都相等并且最后一项不相等,显然成立,所以让
# 第一个列表中的除了尾项以外的元素加上第一个列表的尾项与第二个列表的尾项排序之后的这两项,得到['a', 'c', 'e']
for i in range(len(x)):
for j in range(i, len(x)):
# print('x[i][l-1]: \n', x[i][l-1])
# print('x[j][l-1]: \n', x[j][l-1])
if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
r.append(x[i][:l-1]+sorted([x[j][l-1], x[i][l-1]]))
return r
def find_rule(d, support, confidence, ms=u'--'):
"""寻找关联规则的函数"""
result = pd.DataFrame(index=['support', 'confidence']) # 定义输出结果
# d是DataFrame格式的0-1矩阵
support_series = 1.0*d.sum()/len(d) # 支持度序列
# print('d.sum(): \n', d.sum())
# print('len(d): \n', len(d))
print('support_series: \n', support_series)
column = list(support_series.index)
# column = list(support_series[support_series >= support].index) # 初步根据支持度筛选
# print('column: \n', column)
k = 0
while len(column) > 1:
k = k+1
print(u'\n正在进行第%s次搜索...' % k)
column = connect_string(column, ms)
print('column: \n', column)
print(u'数目:%s...' % len(column))
# prod()函数的作用是连乘,对于DataFrame格式的数据可以选择按行或者按列来连乘,numeric_only=True表示只支持数字间乘积
# Series格式的数据只能按列连乘,不支持numeric_only=True
sf = lambda i: d[i].prod(axis=1, numeric_only=True) # 新一批支持度的计算函数
# 创建连接数据,这一步耗时、耗内存最严重。当数据集较大时,可以考虑并行运算优化。
# map(sf, column)的作用是分别取出column中的每个元素所对应的DataFrame数据然后连乘
# list(map(sf, column))是将map(sf, column)完成的后的数据转换成一个新的列表,列表中的元素都是Series格式
# 然后将新的列表转换成DataFrame格式
d_2 = pd.DataFrame(list(map(sf, column)), index=[ms.join(i) for i in column]).T
print('d_2: \n', d_2)
support_series_2 = 1.0*d_2.sum()/len(d) # 计算连接后的支持度序列
print('support_series_2: \n', support_series_2)
# 通过最小支持度过滤候选k项集集合Ck得到频繁k项集集合Lk
column = list(support_series_2[support_series_2 >= support].index)
support_series = support_series.append(support_series_2)
print('support_series: \n', support_series)
print('column_filter: \n', column)
rule = []
# 从频繁项集项集生成可能关联规则
for i in column: # 遍历可能的推理,如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B?
i = i.split(ms) # i= ['a', 'c', 'e']
for j in range(len(i)):
# i[:j]表示取前j个元素,下标为(0, j-1)
# i[j+1:]表示取后len(i)-(j+1)个元素,下标为(j+1, len(i)-1)
# i[j:j+1]表示取下标为j的元素
# 每次将下标为j为元素作为关联规则的前项,其余的作为关联规则的后项,就形成了一个新的关联规则
rule.append(i[:j]+i[j+1:]+i[j:j+1])
print('rule: \n', rule)
cofidence_series = pd.Series(index=[ms.join(i) for i in rule]) # 定义置信度序列
for i in rule: # 计算置信度序列
# 如 i= ['c', 'e', 'a'],则cofidence_series['c--e--a'] = support_series['a--c--e']/support_series['c--e']
# support_series[ms.join(i[:len(i)-1])]表示取除了最后一个元素外的其它元素组成的关联规则的支持度
cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
print('cofidence_series: \n', cofidence_series)
# 根据置信度筛选关联规则
for i in cofidence_series[cofidence_series > confidence].index:
# 先给每一列都赋值为0.0,不然后面修改值得过程会报错
result[i] = 0.0
result[i]['confidence'] = cofidence_series[i]
result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
print('result_T: \n', result.T)
# 通过降序排序confidence这一列来排序整个DataFrame
result = result.T.sort_values(['confidence'], axis=0, ascending=False,)
return result
(2)调用apriori .py得到结果
# -*- coding: utf-8 -*-
# 使用Apriori算法挖掘菜品订单关联规则
from __future__ import print_function
import pandas as pd
import numpy as np
from apriori import * # 导入自行编写的apriori函数
input_path = 'F:/DataMining/chapter5/menu_orders.xls'
output_path = 'F:/DataMining/chapter5/tmp/apriori_rules.xls' # 结果文件
data = pd.read_excel(input_path, header=None)
print('data: \n', data)
print(u'\n转换原始数据至0-1矩阵...')
print('data_as_matrix: \n', data.as_matrix())
# array = np.array(data)
# a1 = array[0, :]
# print('a1: \n', a1)
# print(pd.Series(1, index=a1[pd.notna(a1)]))
# 匿名函数ct的作用是取出x中不是NAN的元素作为索引列,然后对应的值都为1。
# pd.Series()要求值的个数要么和索引的个数相等,要么只给定一个值然后按照索引的个数复制
ct = lambda x: pd.Series(1, index=x[pd.notna(x)])
# 多维矩阵相当于是列表嵌套列表,所以map(ct, data.as_matrix())的作用是对列表中的每一个列表都执行匿名函数ct,
# 也就是对矩阵的每一行(因为数组的每一行是一个列表)都执行匿名函数ct。
b = map(ct, data.as_matrix())
# python3中map()返回的是迭代器,可以通过list()查看结果
# print('list(b): \n', list(b))
# list(b)中的每一项都是一个Series,print('list(b): \n', list(b))执行完毕后记得注释掉该语句,否则会影响后面语句的执行
data_01matrix = pd.DataFrame(list(b)).fillna(0) # 实现矩阵转换,NAN用0填充
print('data_01matrix: \n', data_01matrix)
print(u'\n转换完毕。')
support = 0.2 # 最小支持度
confidence = 0.5 # 最小置信度
ms = '---' # 连接符,默认'--',用来区分不同元素,如A--B。需要保证原始表格中不含有该字符
# find_rule(data, support, confidence, ms).to_excel(output_path)
result = find_rule(data_01matrix, support, confidence, ms) # 输出结果
print('result: \n', result)
结果如下:
result:
support confidence
e---a 0.3 1.000000
e---c 0.3 1.000000
c---e---a 0.3 1.000000
a---e---c 0.3 1.000000
c---a 0.5 0.714286
a---c 0.5 0.714286
a---b 0.5 0.714286
c---b 0.5 0.714286
b---a 0.5 0.625000
b---c 0.5 0.625000
a---c---e 0.3 0.600000
b---c---a 0.3 0.600000
a---c---b 0.3 0.600000
a---b---c 0.3 0.600000