机器学习之逻辑回归原理以及Python实现

逻辑回归

逻辑回归和线型回归的比较：
1.都是线型模型
2.线型回归的y是连续型的，而逻辑回归是二分类的
3.他们的参数空间都是一致的，信息都蕴含在了w和b中。

1.逻辑回归的原理

1.1 逻辑回归的背景知识

由于逻辑回归的结果是分布在0-1区间，所以在线型回归的基础上做一个映射$f$，即：
$$f(x_{11}{w}_1+x_{12}{w}_2+x_{13}{w}_3+...+x_{1j}{w}_j+...+x_{1m}{w}_m+b)={\hat{y}}_1$$

$$f(x_{21}{w}_1+x_{22}{w}_2+x_{23}{w}_3+...+x_{2j}{w}_j+...+x_{2m}{w}_m+b)={\hat{y}}_2$$

$$f(x_{31}{w}_1+x_{32}{w}_2+x_{33}{w}_3+...+x_{3j}{w}_j+...+x_{3m}{w}_m+b)={\hat{y}}_3$$

$$...$$

$$f(x_{n1}{w}_1+x_{n2}{w}_2+x_{n3}{w}_3+...+x_{nj}{w}_j+...+x_{nm}{w}_m+b)={\hat{y}}_n$$

这个映射函数我们一般用sigmoid函数，函数形式如下所示：
$$f(x)=\frac{1}{1+e^{-x}}$$
函数图像：

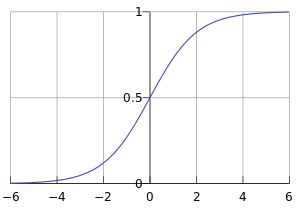
对这个函数求一阶导数：
$$\begin{array}{rl}{f}^{\prime }(x)& =(\frac{1}{1+e^{-x}}{)}^{\prime }\\ & =-\frac{1}{(1+e^{-x}{)}^2}(1+e^{-x}{)}^{\prime }\\ & =\frac{1}{1+e^{-x}}\frac{e^{-x}}{1+e^{-x}}\\ & =f\ast (1-f)\end{array}$$

方便起见：
$$x_i=[x_{i1},x_{i2},x_{i3},...,x_{im}]$$

$$w={[w_1,w_2,w_3,...,w_m]}^T$$

则：
$${\hat{y}}_i=f(x_{i}w+b)=\frac{1}{1+e^{-(x_{i}w+b)}}$$

1.2 逻辑回归原理：

当$x_{i}w+b\to \infty$, $e^{-(x_{i}w+b)}\to 0$, $\frac{1}{1+e^{-(x_{i}w+b)}}\to 1$
故有：
$$p(y_i=1|x_i;w,b)=f(x_{i}w+b)=\frac{1}{1+e^{-(x_{i}w+b)}}\text{\hspace{1em}(1)}$$

$$p(y_i=0|x_i;w,b)=1-f(x_{i}w+b)=\frac{e^{-(x_{i}w+b)}}{1+e^{-(x_{i}w+b)}}\text{\hspace{1em}(2)}$$

为什么说逻辑回归是线型模型？
决策边界来判断
决策边界$p(y_i=0)=p(y_i=1)$即：
$$\frac{1}{1+e^{-(x_{i}w+b)}}=\frac{e^{-(x_{i}w+b)}}{1+e^{-(x_{i}w+b)}}$$
$$1=e^{-(x_{i}w+b)}$$
$$(x_{i}w+b)=0$$
这个决策边界函数是线型函数，所以逻辑回归模型是线型函数。

将（1）和（2）式可合并为：
$$p(y_i|x_i;w,b)=[f(x_{i}w+b){]}^{y_i}[1-f(x_{i}w+b){]}^{(1-y_i)}$$

对所有样本求似然函数：

$$L(w,b)=\prod _{i=1}^n[f(x_{i}w+b){]}^{y_i}[1-f(x_{i}w+b){]}^{(1-y_i)}$$

对数似然函数

$$\log L(w,b)=\log \prod _{i=1}^n[f(x_{i}w+b){]}^{y_i}[1-f(x_{i}w+b){]}^{(1-y_i)}$$

似然函数求取的是最大值，所以损失函数（代价函数）可以定义为：
$$J(w,b)=-\log L(w,b)=-\sum _{i=1}^n{y}_i\log [f(x_{i}w+b)]+(1-y_i)\log [1-f(x_{i}w+b)]$$

1.3 算法求解

接下来求模型的参数$w,b$:
$$\begin{array}{rl}\frac{\partial J(w,b)}{\partial w_j}& =\frac{\partial }{\partial w_j}\{-\sum _{i=1}^n{y}_i\log [f(x_{i}w+b)]+(1-y_i)\log [1-f(x_{i}w+b)]\}\\ & =-\sum _{i=1}^n\{y_i\frac{1}{f(x_{i}w+b)}-(1-y_i)\frac{1}{1-f(x_{i}w+b)}\}\frac{\partial f(x_{i}w+b)}{\partial w_j}\\ & =-\sum _{i=1}^n\{y_i\frac{1}{f(x_{i}w+b)}-(1-y_i)\frac{1}{1-f(x_{i}w+b)}\}f(x_{i}w+b)[1-f(x_{i}w+b)]\frac{\partial (x_{i}w+b)}{\partial w_j}\\ & =-\sum _{i=1}^n\{y_i[1-f(x_{i}w+b)]-(1-y_i)f(x_{i}w+b)\}\frac{\partial (x_{i}w+b)}{\partial w_j}\\ & =-\sum _{i=1}^n\{y_i[1-f(x_{i}w+b)]-(1-y_i)f(x_{i}w+b)\}{x}_{ij}\\ & =-\sum _{i=1}^n\{y_i-f(x_{i}w+b)\}{x}_{ij}\\ & =\sum _{i=1}^n\{f(x_{i}w+b)-y_i\}{x}_{ij}\\ & =\sum _{i=1}^n\{{\hat{y}}_i-y_i\}{x}_{ij}\end{array}$$
同理可得：
$$\frac{\partial J(w,b)}{\partial b}=\sum _{i=1}^{n}f(x_{i}w+b)-y_i={\hat{y}}_i-y_i$$

可以用梯度下降法进行对$w$和$b$进行求解：
$$w_j=w_j-\alpha \sum _{i=1}^n(f(x_{i}w+b)-y_i)x_{ij}$$
$$b=b-\alpha \sum _{i=1}^n(f(x_{i}w+b)-y_i)$$

也可以随机梯度下降法(SGD)：
for i=1 to n:
$$w_j=w_j-\alpha (f(x_{i}w+b)-y_i)x_{ij}$$
$$b=b-\alpha (f(x_{i}w+b)-y_i)$$
当然也可以用批量随机梯度下降法，即循环多次，每次从样本中随机取出一部分样本迭代参数。上式中$\alpha$为学习率。

2.逻辑回归Python实现

2.1 逻辑回归模型实现

import numpy as np

class MyLogisticRegression(object):
    def __init__(self, lr=0.01, n_epoch=50):
        """
        逻辑回归模型，通过随机梯度下降法实现
        :param lr: 学习率，默认值0.01
        :param n_epoch: 训练循环次数，默认值50
        """
        self.lr = lr
        self.n_epoch = n_epoch
        self.params = {'w': None, 'b': 0}

    def __init_params(self, m):
        """
        初始化参数，正态分布
        :param m: 特征维度数，和w的个数相对应
        :return: None
        """
        self.params['w'] = np.random.randn(m)

    def fit(self, X, y):
        """
        训练模型，随机梯度下降法训练模型
        w_j = w_j - lr * (f(x_i @ w) - y_i) * x_ij
        b = b - lr * (f(x_i @ w) - y_i)
        :param X: 训练数据X，shape(n, m), n代表训练样本个数,m代表每个样本的特征维度数
        :param y: 训练数据y, shape(n)
        :return: None
        """
        X = np.array(X)
        # n 样本数量, m 一个样本的特征维度数量
        n, m = X.shape
        self.__init_params(m)

        for _ in range(self.n_epoch):
            for x_i, y_i in zip(X, y):
                for j in range(m):
                    self.params['w'][j] = self.params['w'][j] - self.lr * (sigmoid(np.dot(x_i, self.params['w'].T) + self.params['b']) - y_i) * x_i[j]
                self.params['b'] = self.params['b'] - self.lr * (sigmoid(np.dot(x_i, self.params['w'].T)+ self.params['b']) - y_i)

    def predict(self, X):
        """
        预测模型结果
        :param X: 二维数据，shape(n,m),n代表个数，m代表单个样本的维度数
        :return: y shape(n), 预测结果
        """
        return sigmoid(np.dot(X, self.params['w'].T) + self.params['b'])


def sigmoid(x):
    return 1 / (1 + np.exp(-x))

2.2 结果验证

def get_samples(n_ex=100, n_classes=2, n_in=1, seed=0):
    # 生成100个样本，为了能够在二维平面上画出图线表示出来，每个样本的特征维度设置为1
    from sklearn.datasets.samples_generator import make_blobs
    from sklearn.model_selection import train_test_split
    X, y = make_blobs(
        n_samples=n_ex, centers=n_classes, n_features=n_in, random_state=seed
    )
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.3, random_state=seed
    )
    return X_train, y_train, X_test, y_test


def run_my_model():
    from matplotlib import pyplot as plt
    my = MyLogisticRegression()
    X_train, y_train, X_test, y_test = get_samples()
    my.fit(X_train, y_train)

    y_pred = my.predict(X_test)
    print(y_pred, y_test)

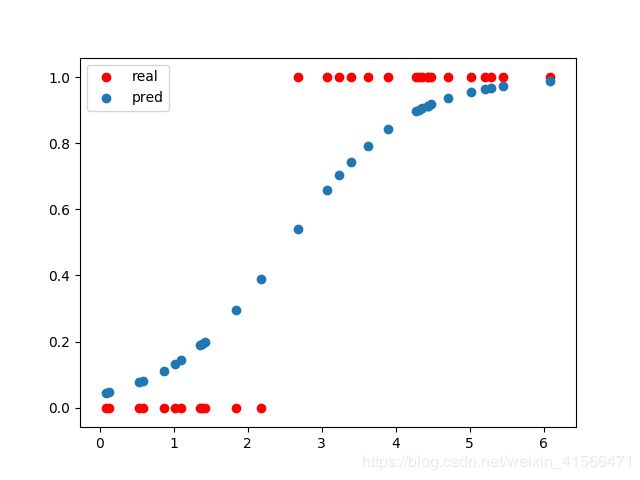
    # 画图
    fig, ax = plt.subplots()
    ax.scatter(X_test, y_test, c='red', label='real')
    ax.scatter(X_test, y_pred, label='pred')
    ax.legend()
    plt.show()

预测结果如下图所示：