收入时间序列——之模型探索篇
前文《收入时间序列——之数学理解篇》已经梳理了时序分析所具备的基本数学原理,现在开始着手探索收入数据的内在规律,主要提出以下几个问题并给予解答。
- 收入时间序列是平稳的吗?(偏)自相关情况如何?
- 收入时间序列有趋势或季节性效应吗?
- 用什么模型拟合效果比较好?
- 有无异方差特征?用GARCH模型效果如何?
- 收入增长率的平稳性情况如何?
下面开始具体探讨过程。
一. 线性模型时序分析步骤
当我们拿到一个时间序列(多半是非平稳的),一般作如下分析流程:
这里稍微留意一下,平稳性检验未通过后,差分运算只是其中一种方法,做完差分再回去通过平稳性检验后,一般会对原序列拟合 模型(图中是对差分后的序列拟合 模型),这里的 就是差分阶数,注意不是差分步数,差分步数是消除季节效应的。
二. 准备程序
为方便调用,将经常调用的绘图和假设检验程序事先定义好:
时序图
def draw_series(timeSeries, title):
fig = plt.figure(figsize=(12,8))
fig.add_subplot()
plt.plot(timeSeries)
plt.title(title)
ADF检验
# Dickey-Fuller检测:
def ADF_test(timeseries):
dftest = adfuller(timeseries, autolag='AIC')
print(dftest)
# 尝试三种类型
dftest_ct = adfuller(timeseries, regression='ct', autolag='AIC')
dftest_c = adfuller(timeseries, regression='c', autolag='AIC')
dftest_nc = adfuller(timeseries, regression='nc', autolag='AIC')
print(dftest_ct,dftest_c,dftest_nc)
LB检验
# 白噪声检验
def LB_test(timeseries):
[[lb], [p]] = acorr_ljungbox(timeseries, lags=1)
if p < 0.05:
print(u"原始序列为非白噪声序列,对应的p值为:%s" % p)
else:
print(u"原始序列为白噪声序列,对应的p值为:%s" % p)
# 带延迟参数
def LB_test_detail(timeseries, lag):
acf, q, p = sm.tsa.acf(timeseries, nlags=lag, qstat=True) ## 计算自相关系数 及p-value
out = np.c_[range(1, lag+1), acf[1:], q, p]
output = pd.DataFrame(out, columns=['lag', "AC", "Q", "P-value"])
output = output.set_index('lag')
print(output)
ACF/PACF图
# 自相关和偏相关图——全部序列
def draw_acf_pacf(timeseries):
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
plot_acf(timeseries, ax=ax1)
ax2 = fig.add_subplot(212)
plot_pacf(timeseries, ax=ax2)
# 自相关和偏相关图——延迟参数
def draw_acf_pacf_lag(timeseries, lags):
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
plot_acf(timeseries, lags=lags, ax=ax1)
ax2 = fig.add_subplot(212)
plot_pacf(timeseries, lags=lags, ax=ax2)
三. 数据处理
# 导入收入表结构
f = open('某店每日收入指标跟踪表.csv', encoding='UTF-8')
# 去掉EXCEL表头
data = pd.read_csv(f, header=[0,1,2])
# 特征选取前三列并重新命名
data = data.iloc[:,0:3]
data.columns = ['日期属性','账期','本日收入']
# 按账期正时序排序
data['账期'] = pd.to_datetime(data['账期'],infer_datetime_format=True)
data = data.sort_values(by=['账期'])
data = data.reset_index(drop=True) #设定一个新的索引列
# 异常数据处理
# 用对应日期属性的收入中位数替换收入小于等于0的样本
for index in data.ix[data['本日收入'] <= 0].index:
for name, group in data['本日收入'].groupby(data['日期属性']):
if data.ix[index, 0] == name:
data.ix[index, 2] = group.median()
# 检验是否还有异常数据
print("非正值情况:\n", (data['本日收入'] <= 0).sum(axis=0).sort_values(ascending=False))
# 重新将账期设为索引
data.set_index('账期', inplace=True)
income_data = data.ix[:,'本日收入']
读入数据,并只保留时间和收入,日期属性是为计算中位数替代异常值,输出的时间序列数据定义为 income_data,是一个 Series 类型。
四. 收入平稳判断
# 收入时序图
draw_series(income_data, '本日收入')
显示上下幅度变化较大,貌似还有一点上升趋势,直观上不易观察出是否平稳:
选取前100天时序,看上去很平稳:
draw_series(income_data[:100], '本日收入')
取全部时序的ACF和PACF图,显示ACF虽然收敛至0但收敛很缓慢;PACF基本在零值附近:
# 自相关图/偏自相关图
draw_acf_pacf(income_data)
再取延迟40阶,很明显ACF除1阶延迟有正相关外,还在6/7/8、13/14/15、20/21/22等延迟阶处呈周期性显著相关;PACF在延迟8阶后基本收敛至2倍标准差以内,但也出现在15阶和22阶显著大于2倍标准差的情况。总体来说,自相关具有非常明显的周期特点:
draw_acf_pacf_lag(income_data, 40)
上图具体分析就是:本日收入和昨天、上周/上上周等的环比当天及前后各一天有显著正相关性。举个例子:今天是周三,和昨天周二、上周二/三/四、上上周二/三/四、以及上上上周二/三/四等收入正相关,可以粗略理解为它涨我也涨,它跌我也跌,有一种线性关系,正相关系数在0.5-0.7左右。随着延迟阶数增大,周环比前后那两天的正相关性大约在一个月以后不显著,唯独周环比的正相关性大约在延迟250天后才不显著。注意这家门店是个老店,说明周环比的正相关性会在8-9个月时间范围内一直显著存在,有长期记忆。我们分别取100阶和365阶延迟的ACF图再看下:
draw_acf_pacf_lag(income_data, 100)
draw_acf_pacf_lag(income_data, 365)
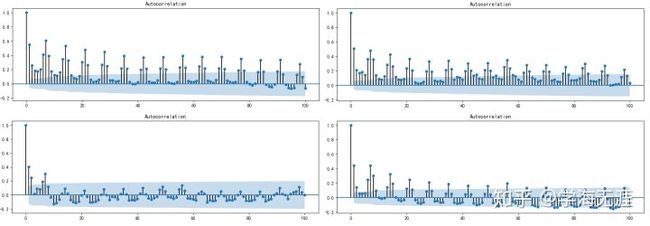
我随机选择了其它4家门店,它们都有明显相似的周期性现象,只不过有2家(上面一行)没有负自相关性,有2家(下面一行)ACF收敛相对较快,分析原因是开店时间较短:
LB检验的p值明显小于0.05,显著拒绝原假设,存在自相关性,说明原序列本身不是白噪声序列:
# 检测白噪声
LB_test(income_data)
原始序列为非白噪声序列,对应的p值为:2.2959168206783413e-52
单位根检验p值为0.0000316,小于0.05,显著拒绝原假设,不存在单位根,属于平稳时序。
# 单位根检验
ADF_test(income_data)
(-4.921922984782108, 3.160487308474228e-05, 21, 838, {'1%': -3.4381774989729816, '5%': -2.8649951426291, '10%': -2.568609799556849}, 19519.837221505346)
在这里,我始终不相信是平稳的,于是踩了一个很深很深的坑,花了很多时间,查阅了很多资料,最终才弄清楚原委,需要单独写一篇文章详细讲解(参见《单位根检验、航空模型、季节模型》)。先继续我原先的操作,同时也相当于做了一个很好的测试。
五. 模型拟合
既然ADF检验结果是平稳,那就直接开始选ARMA模型的参数:
import statsmodels.tsa.stattools as st
order = st.arma_order_select_ic(income_data,max_ar=10,max_ma=10,ic=['aic', 'bic', 'hqic'])
print(order.aic_min_order)
print(order)
结果跑了半个多钟头,虽然设定的AR和MA的上限阈值也只有10,但还是很耗计算资源的:
(10, 9)
'aic_min_order': (10, 9), 'bic_min_order': (7, 8), 'hqic_min_order': (10, 9)
BIC推荐的是AR=7,MA=8(AR是行,MA是列),其值为20092:
AIC推荐的是AR=10,MA=9(AR是行,MA是列),其值为20001:
我们采用AIC准则,用ARMA(10, 9)拟合看下效果(统计领域称为样本内拟合,ML领域习惯称为训练集,这里我单纯是为了寻找规律,就默认全体作为训练集),结果显示真实值和拟合值的均方根误差为17075,误差不算小:
看看残差,整体以及40阶的ACF和PACF图如下:
残差序列图显示均值为0,方差虽有界但振荡很厉害:
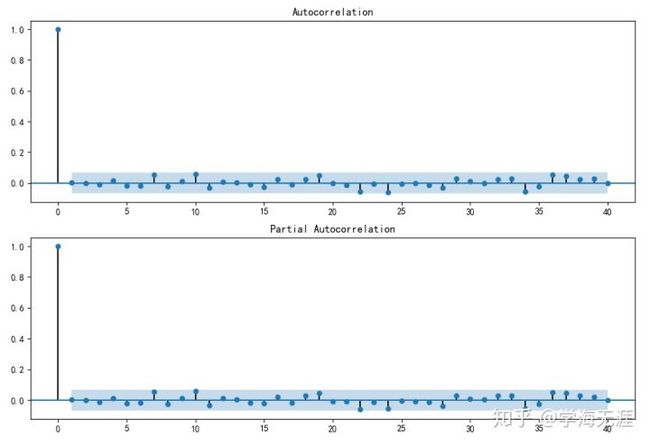
残差检验的确在12阶内都是白噪声,数据虽漂亮,但这里插一句,很显然,选择高阶模型拟合容易造成过拟合,对测试集(样本外数据)拟合的泛化能力会差:
原始序列为白噪声序列,对应的p值为:0.9422545364762434
AC Q P-value
lag
1.0 0.002480 0.005247 0.942255
2.0 -0.000544 0.005499 0.997254
3.0 -0.011663 0.121796 0.989099
4.0 0.013216 0.271321 0.991590
5.0 -0.020769 0.641002 0.986049
6.0 -0.018040 0.920250 0.988456
7.0 0.051981 3.241488 0.861800
8.0 -0.024492 3.757403 0.878321
9.0 0.010084 3.844975 0.921316
10.0 0.056528 6.599900 0.762599
11.0 -0.030970 7.427799 0.763457
12.0 0.008345 7.487987 0.823755
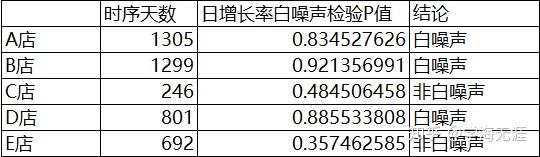
为了进一步验证平稳性,我随机找了其它5家门店,并做了一张表(这里AIC准则下设定的AR和MA阶数上限都是5):
根据上述ARMA模型定阶建议,拟合后对残差进行检验,如下表:
除一家门店未通过外,其它均通过白噪声检验。
不管是老店,还是新店;不管是优质店,还是困难店;上述结果都是一致认为门店收入是一个平稳时序。但从ACF图上看应该是非平稳,因为我们看到ACF不是短期自相关、不是指数下降收敛,且明显有周期为7天的季节效应,所以应该是非平稳序列才对。我们发现,ADF检验有一个假定方差齐性的前提条件,且只针对AR模型,所以它对于异方差序列的平稳检验效果不好,我们不妨验证一下异方差。
六. 异方差检验
考察残差平方,绘制对ARMA(10,9)拟合过后的残差平方时序图,看出波动范围比较大,特别留意纵轴数量级为1e10,这个数值很大很大:
下图是残差平方的ACF/PACF图,显示残差平方在1/2/5/7/23/28阶仍有短期自相关性:
对残差平方进行白噪声混成检验:
原始序列为非白噪声序列,对应的p值为:6.092519718844631e-11
AC Q P-value
lag
1.0 0.223975 42.790568 6.092520e-11
2.0 0.113838 53.857696 2.018133e-12
3.0 0.057050 56.640563 3.066451e-12
4.0 0.058473 59.567406 3.576210e-12
5.0 0.108737 69.700830 1.182736e-13
6.0 0.032036 70.581454 3.106869e-13
7.0 0.165199 94.026113 1.839360e-17
8.0 0.031463 94.877546 4.737981e-17
9.0 0.069649 99.054841 2.443283e-17
10.0 -0.011426 99.167396 7.997408e-17
11.0 -0.012031 99.292342 2.465593e-16
12.0 0.012972 99.437771 7.174372e-16
p值显著小于0.05,拒绝原假设,为非白噪声,说明残差平方具有自相关性,确定存在异方差。从残差平方ACF/PACF图看,可以考虑拟合GARCH(1,1)模型,ARCH模型也被称为波动率模型,可以对波动率进行预测。通过检验出异方差我们也相信ADF检验结果只是一个参考,数据的真相离我们越来越近。
七. ARIMA模型定阶
经过一系列探求真相的艰辛过程,我发现在数理统计方面,R 的功能和效率都要比 python 来的更强大更高效,所以后续有关各种平稳检验、异方差检验、建模等我都将在 R 中调试。
# ARMA手工定阶
library("TSA")
ths_pq = eacf(income_data, 20, 20)
print(ths_pq$eacf)
R 提供了另一种选择p和q参数的方法eacf(),先看结果:
> ths_pq = eacf(income_data, 20, 20)
AR/MA
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 x o o o o x x x o x x x x x x x x x x x x
1 x x o o o x x x x o x o x x x x o o x x x
2 x x x o o o x x x x o o o x x x x o x o x
3 x x o o o o x x x o o o o x x x o o x o x
4 x o o o o o x x x x x x o x o x o x x o x
5 x x x o x x x x x o o x o x o x x o x o x
6 x x x o x x x x x o x x x x x x x o x x x
7 x x x x x x x o o o o o o o o o o x x o o
8 x o x x x o x x o o o o o o o o o o o o o
9 x o o x o o x x o o o o o o o o o o o o o
10 x x o x o o x x o x o o o o o o o o o o o
11 x x x o o x x x o x o o o o o o o o o o o
12 x x x o o x x x o x o o o o o o o o o o o
13 x o x x x x o o o x x o o o o o o o o o o
14 x x x x x x x o o x o o o o o o o o o o o
15 x o x o x x o x o x o o o o o o o o o o o
16 x o x o o x o x x x x x o o o o o o o o o
17 o x x o o o x o x x o x x o o o o o o o o
18 x x x x o o x o x x x o o o o o o o o o o
19 x o x x o x x x x x o x x x x o o o o o o
20 x x o x x o x x x o x x x x o o o o o o o
这是Tsay提供的一种方法,看圆圈形成的右下三角形所在的起始位置,要尽量为圆圈包含,这里(8,8)似乎是最佳选择,当然(7,7)也可以尝试下,(10,9)也没问题。
为了和前面保持一致,选择(10,9)模型:
arimafit<-arima(income_data,order=c(10,0,9),method="ML")
arimafit
# 残差检验
acf(arimafit$residuals,lag.max=40)
残差ACF图(40阶),和之前一致,不仅仅在12阶,40阶内都是白噪声特征:
残差平方ACF图(40阶),存在显著自相关性:
对残差进行McLeod-Li检验,它其实就是用LB统计量检验残差平方:
# 残差McLeod-Li检验ARCH效应(残差平方LB统计量)
# 以下两种调用均可以
McLeod.Li.test(arimafit)
McLeod.Li.test(y=arimafit$residuals)
图形如下:
和之前残差平方检验为非白噪声一致,p值几乎为0,拒绝无自相关性的原假设,说明具有非常明显的ARCH效应。
现在,我们消除季节效应,直接用ARIMA模型进行拟合:
# ARIMA自动定阶,并拟合
library(forecast)
autoarima = auto.arima(income_data,trace=T)
autoarima
先看自动给出的参数效果,其AIC值为19865,比之前未作差分的AIC=20001要好:
Best model: ARIMA(2,0,4)(0,1,1)[7]
Coefficients:
ar1 ar2 ma1 ma2 ma3 ma4 sma1
0.1748 -0.4091 0.5092 0.6710 0.4342 0.2757 -0.9014
s.e. 0.1746 0.0953 0.1669 0.1206 0.0597 0.0454 0.0325
sigma^2 estimated as 743158892: log likelihood=-9924.56
AIC=19865.12 AICc=19865.29 BIC=19903.11
这里的(0,1,1)[7]表示季节效应1阶7步差分,并用ARMA(0,1)模型,[7]是对应我开头设置frequency相一致:
income_data = ts(income_data,frequency = 7)
总体效果如下:
# 使用tsdiag查看拟合后的效果
tsdiag(autoarima)
能看出ACF在7/14阶存在自相关性,说明模型拟合不是很好,再尝试 模型,明显好过 ,AIC值为19804:
> arimatest<-arima(income_data,order=c(2,0,4),seasonal=list(order=c(1, 1, 1),period=7))
> arimatest
Call:
arima(x = income_data, order = c(2, 0, 4), seasonal = list(order = c(1, 1, 1),
period = 7))
Coefficients:
ar1 ar2 ma1 ma2 ma3 ma4 sar1 sma1
-0.2888 0.4461 0.9406 0.0690 0.0055 0.0975 0.3464 -0.9545
s.e. 0.1353 0.1306 0.1364 0.2017 0.1264 0.0561 0.0392 0.0112
sigma^2 estimated as 683882070: log likelihood = -9893.37, aic = 19804.74
那么,残差的ARCH效应得到缓解了吗?我们作一系列异方差检验,通过McLeod-Li检验发现残差平方仍不是白噪声:
qq分布图显示非正态:
残差平方的ACF图相比之前有所改善,但仍存在自相关性:
我们再试试之前做平稳性检验时观察到的季节模型(参见《单位根检验、航空模型、季节模型》),其AIC值为19813,和 相比AIC没有多多少。总的来说,我们发现经季节差分后,AIC不但下降得到改善,同时模型阶数(1,3)×(1,1)也要比之前没有季节差分的模型阶数(10,9)低不少。
> arima1<-arima(income_data,order=c(1,0,3),seasonal=list(order=c(1, 1, 1),period=7))
> arima1
Call:
arima(x = income_data, order = c(1, 0, 3), seasonal = list(order = c(1, 1, 1),
period = 7))
Coefficients:
ar1 ma1 ma2 ma3 sar1 sma1
0.8198 -0.1747 -0.2040 -0.0918 0.2696 -0.9507
s.e. 0.1112 0.1159 0.0927 0.0585 0.0415 0.0114
sigma^2 estimated as 694178972: log likelihood = -9899.63, aic = 19813.26
综上,我们发现不论是用高阶ARMA模型,还是经季节差分后的低阶ARIMA模型,都无法避免收入序列的异方差性,存在随时间波动的不确定性。回顾收入分布的尖峰厚尾,说明日收入序列有明显的ARCH效应,这种效应说明了其残差本身虽检验为白噪声,但由于并不是同分布,所以不满足方差齐性的条件,最小二乘估计未必准确有效,拟合精度值得怀疑。
八. GARCH模型拟合
现在考虑残差residuals(arimatest)条件异方差的拟合模型。通过观察残差平方的PACF图,发现前两阶自相关显著,同时在7阶也显著,我们先考虑ARCH(2):
library("fGarch")
m1 = garchFit(~garch(2,0),data=residuals(arimatest),cond.dist="norm") # 正态
Error in solve.default(fit$hessian) :
system is computationally singular: reciprocal condition number = 5.25237e-18
提示奇异矩阵,原因在数据,我们取对数后不再报错,相应的模型变为ARIMA(1,0,0)×(1,1,1,7),对应残差平方PACF图如下:
直接拟合GARCH(1,1)模型:
library("fGarch")
m1 = garchFit(~garch(1,1),data=residuals(arima_log),cond.dist="norm") # 正态
acf(residuals(m1),lag=40)
pacf(residuals(m1)^2,lag=40)
结果如下:
这说明,应用正态分布形式的新息所估计的模型并不充分。还记得那个标准残差 么,这里 可以选择正态、学生t、广义误差等分布形式, 对应上面ARIMA模型的残差。我们分别尝试这几种分布,得出以下表格:
最后,我们发现AIC和BIC都指认std学生t分布方式拟合效果最好:
Conditional Distribution:
std
Coefficient(s):
mu omega alpha1 beta1 shape
0.015259 0.037861 0.271543 0.625421 3.005865
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.01526 0.01034 1.476 0.1401
omega 0.03786 0.01468 2.579 0.0099 **
alpha1 0.27154 0.08552 3.175 0.0015 **
beta1 0.62542 0.09329 6.704 2.03e-11 ***
shape 3.00587 0.37093 8.104 4.44e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Log Likelihood:
-340.1342 normalized: -0.3955049
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 504.2026 0
Shapiro-Wilk Test R W 0.9445162 0
Ljung-Box Test R Q(10) 17.61962 0.06172919
Ljung-Box Test R Q(15) 26.67234 0.03152222
Ljung-Box Test R Q(20) 31.19687 0.05264448
Ljung-Box Test R^2 Q(10) 37.94772 3.875518e-05
Ljung-Box Test R^2 Q(15) 54.9896 1.793052e-06
Ljung-Box Test R^2 Q(20) 58.29684 1.302321e-05
LM Arch Test R TR^2 47.25082 4.217742e-06
除均值方程 外,其它参数均显著,所以表达式为:
上述 是取对数后用季节ARIMA模型拟合后的残差序列,均值方程参数不显著异于零,因此它直接等于扰动 , 是符合自由度为3的学生t分布的新息,条件异方差 表达式是波动率方程,它和过去上一个时刻的扰动平方及条件方差呈现简单的线性关系。GARCH模型拟合后的标准残差平方 的ACF图如下,前6阶均无相关性,说明得到明显改善:
标准残差QQ分布图,和之前的QQ图相比具有更明显的正态性,除一些异常点外:
残差(扰动)原序列时序图:
条件异方差(波动率)序列,能看出某些时刻波动非常大,不难猜到这些可能是节假日业务冲击收入指标的时刻,也有可能是收入迅速下滑的时刻:
标准化残差,和扰动原序列看上去并无二异,正态性不强,说明模型拟合的不充分:
Jarque-Bera和Shapiro-Wilk检验p值为0,均拒绝了原假设,说明标准残差不是正态分布,模型仍有待优化,这也说明其扰动凭借低价的GARCH无法充分拟合,或者需要寻找其它形式的GARCH模型。由于我们只是探索数据的异方差性质,目的不是为了估计这样的波动数值,故本文不再深入分析。
综上,GARCH模型确实捕捉到了波动的自回归特性(波动聚集性)和收入对数分布的尖峰特性,但是,它的主要缺点在于它的对称性,因此无法捕捉分布的非对称特性与杠杆效应。GARCH模型中出现波动聚集性高度符合直觉,这也就对应解释其尖峰特性。
九. 收入日增长率平稳判断
出于好奇,还想看看增长率是什么情况,类似但有别于金融数据经常分析投资收益率,收入的日增长率不会累计统计(类似于复利),所以我们沿用业务习惯的增长率计算方式:
# 收入增长率
income_rate = (income_data.shift(-1) - income_data) / income_data
income_rate.dropna(inplace=True)
print(income_rate.describe())
ACF图显示存在 7 天周期的自相关性,白噪声检验为1阶是白噪声,高于1阶则不是:
原始序列为白噪声序列,对应的p值为:0.7620824142929394
(-4.01414701674605, 0.0013382183047012776, 20, 838, {'1%': -3.4381774989729816, '5%': -2.8649951426291, '10%': -2.568609799556849}, 1805.8214582071332)
AC Q P-value
lag
1.0 -0.010312 0.091656 7.620824e-01
2.0 -0.253491 55.546738 8.673197e-13
3.0 -0.078391 60.856260 3.857376e-13
4.0 -0.052310 63.223286 6.089904e-13
5.0 -0.233721 110.531361 3.163736e-22
6.0 0.018234 110.819628 1.372901e-21
7.0 0.664187 493.765345 1.754972e-102
8.0 0.019656 494.101129 1.296564e-101
9.0 -0.222481 537.169896 6.264061e-110
10.0 -0.070382 541.485152 5.949059e-110
11.0 -0.051042 543.757359 1.471100e-109
12.0 -0.222313 586.913309 6.597362e-118
ADF检验为平稳,KPSS检验除1%显著水平外,其它水平下为非平稳:
(-4.330041211384692, 0.0028245844060121286, 20, 838, {'1%': -3.9696139315814714, '5%': -3.415742085237588, '10%': -3.1301410687829927}, 1805.2799530319767) (-4.01414701674605, 0.0013382183047012776, 20, 838, {'1%': -3.4381774989729816, '5%': -2.8649951426291, '10%': -2.568609799556849}, 1805.8214582071332) (-1.924218490355994, 0.05186032886261765, 20, 838, {'1%': -2.5684131839645477, '5%': -1.941325263784454, '10%': -1.6165068765453274}, 1816.6329747210261)
Result of KPSS Test:
(0.642504998690305, 0.01877227284633591, 21, {'10%': 0.347, '5%': 0.463, '2.5%': 0.574, '1%': 0.739})
Test Statistic 0.642505
p-value 0.018772
Lag Used 21.000000
Critical Valuse (10%) 0.347000
Critical Valuse (5%) 0.463000
Critical Valuse (2.5%) 0.574000
Critical Valuse (1%) 0.739000
dtype: float64
这说明,这家门店的日增长率和日收入性质一样,都是非平稳的,也都不是白噪声,考虑到周期性,如果建模需先作 7 步差分。
为了进一步验证日增长率的平稳性,仍然是另选5家门店,做了如下表和ACF图:
结果显示:大部分门店的日收入增长率是一个平稳时序,其中部分还是纯随机序列(白噪声),验证它们在8阶以内p值均大于0.05,本案这家门店的日增长率呈周期自相关应该为个例。事实上,收入增长率平稳很容易能从数学上得到解释:我们之前定义收入增长率 ,改写为 ,两边再取对数 ,就相当于对增长率平移一个单位后取对数,它的效果等价于对日收入取对数然后一阶差分,而我们容易验证取对数并不能改变数据的季节特征,但差分可以。所以,对日收入数据取对数后,再一阶差分,能消除一定的季节效应,从而增加平稳性,如果有兴趣可以自行测试。
十. 结论
- 日收入存在周期为 7 天延迟的正自相关性,有长期记忆,是一个非平稳时间序列。转化为业务语言可以这样来理解:无论今天是星期几,今天的收入都可参考上周、上上周......上个月......半年前...同日的收入情况,它们线性关联度很高,八九不离十差不多。日收入在去除周期特征后,可以用一个包含短期的过去收入的线性组合及过去误差的线性组合来近似接近,再剩下部分就是一个没有任何规律的正常随机波动。
- 日收入存在显著季节效应,周期为 7 天,未发现有明显的趋势效应。如果非要看趋势的话,可以当作每天增长9块7角钱的幅度,一年增加3500元,这对于一家优质门店基本也可以忽略不计了。
- 通过ARMA(10,9)、ARIMA(5,0,5)×(0,1,0,7)、ARIMA(2,0,4)×(0,1,1,7)以及ARIMA(2,0,4)×(1,1,1,7)比对,发现经过模型拟合后均可达平稳,从AIC值来看,ARIMA(2,0,4)×(1,1,1,7)拟合效果最好。
- 日收入存在显著ARCH条件异方差效应,这说明门店收入除去平稳信息后,仍存在随时间变化的波动扰动。
- 日收入经取对数并经ARIMA季节模型去除线性信息后,其残差扰动可通过一个应用学生t分布新息的GARCH(1,1)模型拟合,虽然模型拟合不是很充分,但可捕捉到条件异方差对尖峰的解释,也正由于其对称性的缺陷导致无法解释非对称特性,比如增长迅速下降缓慢。
- 日收入增长率总体可视作是一个平稳序列,甚至是白噪声,也就是完全无规律正常波动,个例门店的日增长率有自相关性或不平稳,说明有其它因素在影响收入增长率的波动。