R语言基本画图——最常用绘图函数速查

导读
本文是描述性分析画图篇，对于记性不大好的我，每次画图的时候都会忘掉一些参数怎么设置，所以一直想有一份R画图大全，包含所有绘图函数的参数解释和详细例子。等是等不到了，只能自己动手整理一份！翻了一遍R函数文档，历时n天终于整理好了。。啾咪，这篇文章超级方便速查R语言画各种图的用法，包括箱线图散点图柱状图相关图等等所有重要图表的用法等，真的超级详细了。。

一、画图前需要明确的事

数据报告要包含研究目的、描述性分析、特征工程、建模分析、模型检验、模型对比的过程，最后需要加上最重要的结论和建议。其中数据处理的第一步就是描述性分析。关于描述性分析具体怎么写以及通过统计量进行描述的内容，我在前一篇文章已经大致梳理过，详见数据分析报告-经典统计量的描述分析。这次就重点介绍如何利用统计图表来对变量进行描述性分析。

描述性分析通常要解决的问题无非是两个，一是要描述单个变量的特征还是几个变量之间的关系？二是变量是定性变量还是定量变量？明确这两点后图表就易于确定了。

下面依旧主要用上一篇文章的数据集，来自狗熊会(公众号:CluBear)的二手市场上在售的1289条的汽车的10项指标数据，自变量包括汽车描述，排量，性能，级别，车门，车座，马力，发动机和前制动类型等10个变量定因变量为汽车的价格，处理后增加了年份变量，探究汽车价格的关键影响指标。

变量类型	变量名	详细说明	取值范围	备注
因变量	在售价格	单位：万元	1.3~280.0
自变量	描述	汽车品牌与年份及关键字	文字信息
	排量	单位：升	1.3~6.2
	性能	定性变量，2个水平	手动，自动	手动约占28%，自动72%
	级别	定性变量，5个水平	小型，紧凑型，中型，中大型，大型	左边按照从小到大排序
	车门	整数变量	2,3,4,5	存在部分数据偏差
	车座	整数变量	4,5,7,8
	马力	连续变量	85~575
	发动机	定性变量，7个水平	L3，L4，V5，L6，V8，H4，L5	代表不同的气缸排列方式
	前制动类型	定性变量，2个水平	盘式，通风盘式	制动方式，通风盘式造价较高
	年份	整数变量	2004-2017

R语言自带的graphics就有很多绘图函数，如果更高级的作图还可以利用ggplot2包，这个包具体后面再说，今天先用基础函数来写画图

二、单变量绘图

1. 直方图

直方图通过将数值型的变量分为几组，显示对应组内的频数或者频率来刻画变量的分布情况。所以直方图通常用来刻画连续型变量的分布情况，并且函数可以用由hist(x)生成

hist(x, breaks = "Sturges",
     freq = NULL, probability = !freq,
     include.lowest = TRUE, right = TRUE,
     density = NULL, angle = 45, col = NULL, border = NULL,
     main = paste("Histogram of" , xname),
     xlim = range(breaks), ylim = NULL,
     xlab = xname, ylab,
     axes = TRUE, plot = TRUE, labels = FALSE,
     nclass = NULL, warn.unused = TRUE, ...)

所有的函数里面都会有很多参数可以控制调节，类似颜色字体x轴y轴范围等参数都是相通的，所以这边列出hist函数里面最关键的几个参数：

• freq：TRUE表示y轴为频数，FALSE时表示显示频率，当且仅当间隔是等距的（且未指定概率）时，默认值为TRUE，所以平时还是设定一下freq的值比较好
• breaks：控制划分的间隔 ，可以指定以哪些节点作为断点划分区间，可以是给出直方图单元格之间的断点，或给出分组组数，比如breaks=12，指定分12组，比如breaks=seq(0,10,by=1)是指定间隔为0、1、2…10

马上用我们二手车数据的价格举例说明如何绘制直方图：

#par函数可以将几张图放在一张纸上，下面表示一行两列
par(mfrow=c(1,2))
hist(价格,
     breaks = c(0,10,20,30,40,50,60,70,80,100,300),
     xlim=c(0,100),
     freq=TRUE,
     main='价格直方图',
     xlab = '汽车价格',
     ylab = '频数',
     col = 'lightblue')
     
hist(log(价格),
     main='对数价格直方图',
     xlab = '对数价格',
     ylab = '频数',
     col = 'lightblue')

直方图可以很好地看出汽车价格的整体分布是右偏的，大部分集中在低价分段，这类明显符合长尾分布的变量可以考虑取对数后观察是否符合正态分布，后续的建模也可以用对数价格去代替价格

2. 核密度图

核密度估计是用来估计变量的概率密度的一种办法，对应就是核密度图，听着很高大上，其实就是把直方图的组数增加到无穷大以后得到的图，可以相对准确地刻画分布，很多时候核密度图和直方图无需同时展示，根据实际情况挑选，两者表达的是一个意思。

density(x, bw = "nrd0", adjust = 1,
        kernel = c("gaussian", "epanechnikov", "rectangular",
                   "triangular", "biweight",
                   "cosine", "optcosine"),
        weights = NULL, window = kernel, width,
        give.Rkern = FALSE,
        n = 512, from, to, cut = 3, na.rm = FALSE, ...)

• kernel：表示用于估计的核函数，一般选择高斯函数

#核密度图
#核密度图
par(mfrow=c(1,2))
hist(log(价格),
     main='对数价格直方图',
     xlab = '对数价格',
     ylab = '频数',
     col = 'lightblue')
plot(density(log(价格)),
     main='对数价格核密度图',
     )

比较直方图和密度图可以看到整体趋势是一样的，密度图相当于对直方图做很细的划分得到的，整体上看对数价格的密度函数和正态分布还是很相似的

3. 饼图

饼图常用来比较定性变量中不同类型的占比，面积越大对应比例就越高，但是从某种意义上不推荐使用饼图，因为人们对于面积的感知是比较迟钝的，有时也可以考虑用环形图或者是条形图来代替饼图的功能。plotrix包中还有画3d饼图的函数，但是这种饼图就比较花里胡哨 ，没有必要去使用。一个简单的二维饼图为pie函数

pie(x, labels = names(x), edges = 200, radius = 0.8,
    clockwise = FALSE, init.angle = if(clockwise) 90 else 0,
    density = NULL, angle = 45, col = NULL, border = NULL,
    lty = NULL, main = NULL, ...)

一般我们直接调用函数就可以了，由于x表示每个扇形的面积，所以对于定性变量我们需要利用table函数先汇总再画图

par(mfrow=c(1,2))
pie(table(级别),main='车型占比饼图')
#利用RColorbrewer包改颜色
pie(table(级别),main='车型占比饼图',col=brewer.pal(5,'Pastel1'))

三、多变量绘图

刚才说的都是单个变量如何刻画其分布，但是我们经常需要关注双变量间关系（二元关系）和多变量间关系（多元关系），比如以下问题我们就需要一些新的图形来帮助我们

汽车价格与级别的关系是怎样的？
如何在一个图形中展示汽车价格、排量和性能三者之间的关系？
如何在单幅图中展示一堆变量的相关性？它又如何帮助你理解数据的结构呢？

1. 条形图

条形图非常适用于描述定性变量的分布情况，它常常与table函数一起用，由于人眼对柱子的高度比对面积敏感，所以对单个变量，条形图有时就可以代替饼状图，也可以对两个变量画分组的条形图，更好地观察变量之间的联系，具体函数参数如下

barplot(height, width = 1, space = NULL,
        names.arg = NULL, legend.text = NULL, beside = FALSE,
        horiz = FALSE, density = NULL, angle = 45,
        col = NULL, border = par("fg"),
        main = NULL, sub = NULL, xlab = NULL, ylab = NULL,
        xlim = NULL, ylim = NULL, xpd = TRUE, log = "",
        axes = TRUE, axisnames = TRUE,
        cex.axis = par("cex.axis"), cex.names = par("cex.axis"),
        inside = TRUE, plot = TRUE, axis.lty = 0, offset = 0,
        add = FALSE, ann = !add && par("ann"), args.legend = NULL, ...)

• height：一个向量或值矩阵，如果height是向量，则绘图由一系列柱子组成，这些矩形柱的高度由向量中的值指定。 如果height是一个矩阵，则该图的每个条形图都对应于一列高度，该列中的值给出了构成该条形图的堆叠子条形图的高度。
• width：柱子的宽度
• space：柱子之间的宽度
• beside：控制是堆砌条形图还是分组条形图
• horiz：控制柱子方向是竖直还是水平，默认垂直
• names.arg：每个柱子的名称。 如果省略此参数，则自动从height的names属性中获取名称
• legend：图例

先画对于单个定性变量的条形图，需要利用table函数将其转换为整合的形式再画图，不能直接把数据输入进去

counts<-table(级别)
counts
>级别
  小型 紧凑型   中型 中大型   大型 
   160    669    319    133      4 
   
par(mfrow=c(1,2))
barplot(counts,
        main = '竖直条形图',
        #减小x轴标签的字体
        cex.names=0.7,
        legend=rownames(counts), 
        col=brewer.pal(8,'Blues')[c(2,4,5,7,8)]
       )
barplot(counts,
        main = '水平条形图',
        cex.names=0.7,
        #使用las旋转标签方向
        las=2,
        horiz=TRUE,
        col=brewer.pal(8,'Blues')[c(2,4,5,7,8)]
       )

一个简单的条形图，我们就可以从图上看出紧凑型二手车最多，其次是中小型的车，大型车的数量较少，说明紧凑型是市场竞争比较激烈的分段。

如果我们的数据是一个矩阵而不是一个向量，则barplot将画一幅堆砌条形图或分组条形图。如果 beside=FALSE （默认值），则矩阵中的每一列都将生成图中的一个条形，各列中的值对应堆砌的“子条”的高度。如果 beside=TRUE ，则矩阵中的每一列都表示一个分组，各列中的值将并列摆放，比如以下的例子

counts<-table(级别,性能)
counts
#数据如下形式
>        性能
级别     手动 自动
  小型     88   72
  紧凑型  237  432
  中型     32  287
  中大型    2  131
  大型      0    4
  
par(mfrow=c(1,2))
barplot(counts,
        main = '堆砌条形图',
        col=brewer.pal(8,'Blues')[c(2,4,5,7,8)]
       )

barplot(counts,
        main = '分组条形图',
        beside=TRUE,
        col=brewer.pal(8,'Blues')[c(2,4,5,7,8)]
       )
#自定义标签的格式
legend('topleft',pch=15,rownames(counts),col=brewer.pal(8,'Blues')[c(2,4,5,7,8)])

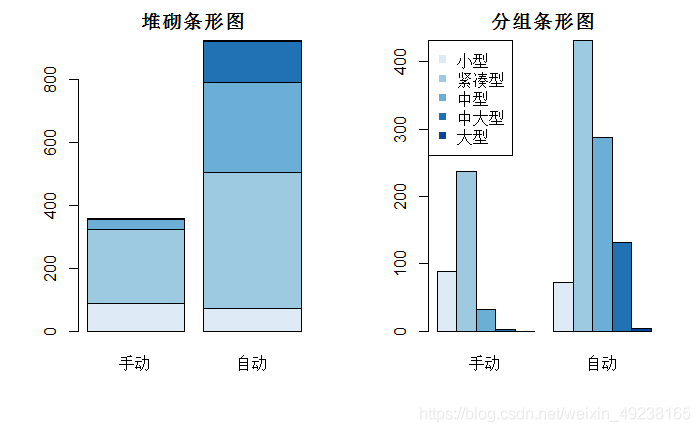
对于级别和性能两个变量画条形图可以看出，自动挡总体车型比手动挡多，相同点在于，无论是在手动挡还是在自动挡中紧凑型都是最集中的部分，但是不同点在于手动挡中很少存在中大型或者大型的车，而自动挡的汽车中虽然大型还是少数，但是较大的汽车还是有不少的。

2. 箱线图

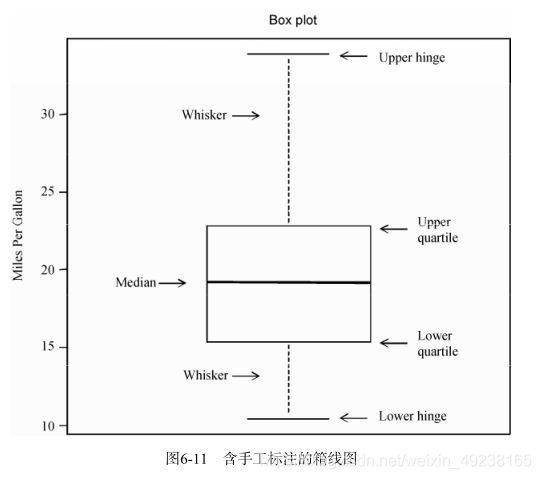
箱线图通过绘制连续型变量的五数总括，即最小值、下四分位数、中位数、上四分位数（第75百分位数）以及最大值，描述了连续型变量的分布。箱线图能够显示出可能为离群点（范围±1.5*IQR以外的值，IQR表示四分位距，即上四分位数与下四分位数的差值）的观测。以下这张图就是箱线图的解读方式，通常我们通过比较箱体的位置就可以发现分布的差异。箱线图主要用在研究连续变量或者连续变量关于定性变量的关系上。

boxplot(x, ..., range = 1.5, width = NULL, varwidth = FALSE,
        notch = FALSE, outline = TRUE, names, plot = TRUE,
        border = par("fg"), col = NULL, log = "",
        pars = list(boxwex = 0.8, staplewex = 0.5, outwex = 0.5),
         ann = !add, horizontal = FALSE, add = FALSE, at = NULL)

• varwidth：默认值FALSE，表示箱子一样宽，TRUE时表示箱体宽度与样本大小成正比，数据越多箱子越宽
• notch：控制箱子是否有凹槽
• x：输入的值为一个向量或者一个函数formula，用~表示函数

par(mfrow=c(1,2))
#表示对数价格关于级别的箱线图
boxplot(log(价格)~级别,col=brewer.pal(5,'Blues'),varwidth=T)
#价格关于不同变量的变化
boxplot(log(价格)~发动机,col=brewer.pal(5,'Blues'))

利用箱线图绘制对数价格分别关于级别和发动机的分布情况，可以看到左图中价格的分布是随着车型的增大而增大的，箱子宽的代表样本比较多，可以看出紧凑型的汽车较多，总体上散落在四分位数外的异常点相对也较少。而右图中不同发动机对应的汽车价格分布差异就较大了，箱子比较长的比如L4就是价格分布比较分散极值点也多，箱子短的比如V8就是价格相对集中而且偏高，箱线图很易于比较不同发动机类型的差异

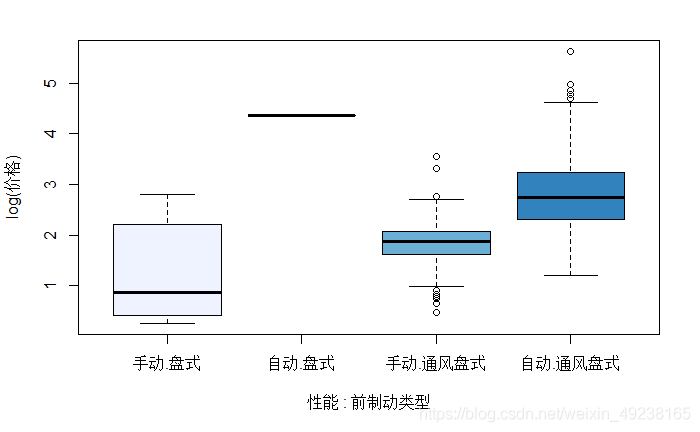
箱线图很强大的一个功能是研究两个因子的关系，比如说现在想观察价格关于级别和前制动类型的关系，我们可以这样实现

boxplot(log(价格)~性能*前制动类型,col=brewer.pal(5,'Blues'))

可以看出盘式的汽车是不存在于自动挡中的，所以图上呈现出一条直线，整体上通风盘式的汽车比盘式要贵，但是通风盘式的汽车中自动挡比手动挡贵。

但是我们也可以看出两个因子变量的箱线图并不是适用于所有数据，否则像上图一样出现缺失的情况就很难看，最佳情况是每个类型变量有2/3个水平，并且这两个变量之间存在一定相关性，可以呈现出不同的分布情况

3. 折线图

折线图是一种很易于观察数据的变化趋势的图形，如果数据集存在时间变化，就可以考虑折线图来绘制。通过plot函数就可以创建，plot也是RY语言作图最基本的一个函数，涵盖了众多功能，通过type参数决定绘图类型

plot(x, y, type=...)
type
what type of plot should be drawn. Possible types are
"p" for points,
"l" for lines,
"b" for both,
"c" for the lines part alone of "b",
"o" for both ‘overplotted’,
"h" for ‘histogram’ like (or ‘high-density’) vertical lines,
"s" for stair steps,
"S" for other steps, see ‘Details’ below,
"n" for no plotting.

type=p表示绘制散点，type=l表示绘制线条，type=b表示点线都画，这三种是比较常用的，下面一张图可以参考

如果我们想画小型汽车价格对于时间变化的折线图，那么可以这样

library(dplyr)
#先生成按级别和时间分类的平均价格表counts
counts<-suv_data%>%
        group_by(时间,级别)%>%
        summarise(avg=mean(价格))%>%
        arrange(级别,时间)
#注意！pipe生成的数据集是tibble型的数据集，如果直接用plot会导致不能修改字体颜色等格式，所以得转换一下
counts<-as.data.frame(counts)
counts$时间<-as.numeric(as.character(counts$时间))
#生成小型汽车的价格折线图
plot(subset(counts,级别=='小型')[,c(1,3)],
     type='b',
     main='小型汽车价格折线图',
     pch=15,lty=1,
     col=brewer.pal(5,'Set2')[1])

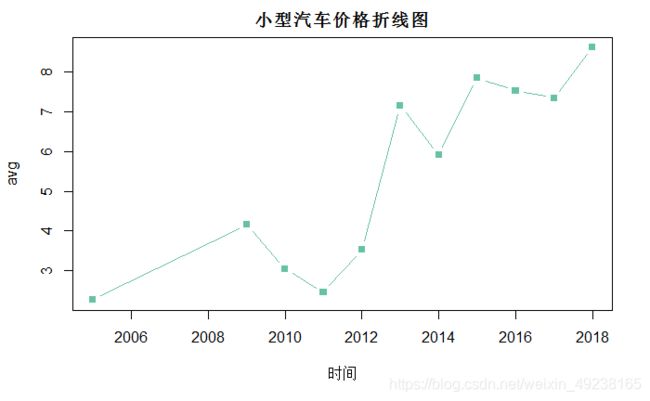
小型汽车的价格折现波动趋势明显，中间降低的几年很大情况是由于样本数量较少，所以导致平均数值不够稳健，出现强烈波动，我们也可以看到整体价格并不是一直上升，在2016年左右也有放缓的趋势。那么如果我们想比较一下小型、中型大型的汽车价格趋势呢？
需要注意的是plot并不能直接分组操作，所以相对来说在一张图上画多个折线图较为繁琐，我们可以通过lines函数一起完成叠加

#先根据x轴y轴的取值范围生成空白画布，
plot(c(2004,2018),c(0,150),
     type='n',
     xlab='时间',
     ylab='价格',
     main='价格时间折线图')
#通过lines添加折线图
lines(subset(counts,级别=='小型')[,c(1,3)],type='b',pch=15,lty=1,col=brewer.pal(5,'Set2')[1])
lines(subset(counts,级别=='紧凑型')[,c(1,3)],type='b',pch=16,lty=2,col=brewer.pal(5,'Set2')[2])
lines(subset(counts,级别=='中型')[,c(1,3)],type='b',pch=17,lty=3,col=brewer.pal(5,'Set2')[3])
lines(subset(counts,级别=='中大型')[,c(1,3)],type='b',pch=18,lty=4,col=brewer.pal(5,'Set2')[4])
lines(subset(counts,级别=='大型')[,c(1,3)],type='b',pch=19,lty=5,col=brewer.pal(5,'Set2')[5])
#自定义添加图例
legend('topleft',legend=c('小型','紧凑型','中型','中大型','大型'),pch=15:19,lty=1:5,col=brewer.pal(5,'Set2'))

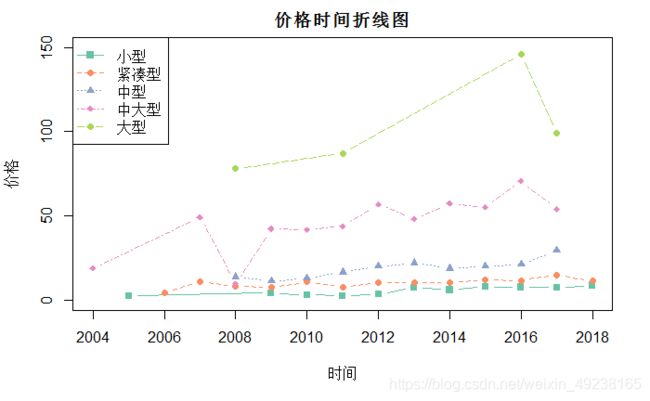
放到整张图上来看，小型汽车的波动就没有那么剧烈了，每一年内大型汽车都比小型汽车价格更高，从波动情况来看中大型的车不稳定因素较强。这张折线图对比性就很明显，非常适用于描述性分析。

4. 散点图

散点图可以很好地展现两个数值型变量之间的关系，是正相关还是负相关亦或是不相关，都可以通过散点图及其拟合线观察，除了刚提到的plot函数可以实现，car包里有一个全能的函数scatterplot可以绘制散点图，具体用法：

scatterplot(x, y, boxplots=if (by.groups) "" else "xy",
        regLine=TRUE, legend=TRUE, id=FALSE, ellipse=FALSE, grid=TRUE,
        smooth=TRUE,
        groups, by.groups=!missing(groups),
        xlab=deparse(substitute(x)), ylab=deparse(substitute(y)),
        log="", jitter=list(), cex=par("cex"),
        col=carPalette()[-1], pch=1:n.groups,
        reset.par=TRUE, ...)

重要的参数有以下几个：

• boxplots：如果为“ x”，则在该图下方绘制x轴变量的箱线图； 如果为“ y”，则在图的左侧绘制y轴变量的箱线图； 默认为“ xy”，绘制两个箱线图
• regLine：绘制拟合的回归线。 如果regLine = FALSE，则不会画线。 如果为TRUE（默认值），则画OLS回归的拟合线。
• ellipse：绘制置信椭圆， fill和fill.alpha可以控制是否填充椭圆以及填充的透明度。
• smooth：绘制平滑器。如果smooth = TRUE，则将对未分组的数据绘制均值函数和方差函数，而仅对分组的数据绘制均值函数。 默认的平滑器是loessLine，用的是stats包中的loess函数，还可以选择分位数回归quantreg
• log：控制是否要对x或y取对数

比如我们现在想绘制汽车对数价格和排量之间的关系， 并且添加loess拟合线以及价格和排量的箱线图，就可以利用散点图把想要的绘制在一张图上

scatterplot(价格~排量,
              lwd=2,
              log='y', 
              smooth=TRUE,
              col=brewer.pal(2,'Set2'),
               main='添加loess拟合线的散点图'
              )

除了散点以外，直线代表的是回归线，虚线是loess平滑线，可以看出价格随着排量整体还是呈现一个上升趋势的，但其实我们可以看出散点并不是都集中在回归线附近，因此可以考虑改用分位数拟合线的方法。分位数回归是研究变量的分位数关于影响因子的变化，而最常见的OLS回归则是研究变量均值的所受的影响，具体相关知识还挺丰富的，这里只是做个绘图展示。

scatterplot(价格~排量,
              lwd=2,
              boxplots='xy',
              log='y', 
              smooth=list(smoother=quantregLine),
              col=brewer.pal(2,'Set2'),
              main='添加分位数拟合线的散点图'
              )

#只画置信椭圆
scatterplot(价格~排量,
              lwd=2,
              boxplots=FALSE,
              log='y', 
              smooth=FALSE,
              regLine=FALSE,
              ellipse=TRUE,
              col=brewer.pal(2,'Set2'),
              main='添加置信椭圆的散点图'
              )

还可以按性能分组绘制价格关于排量的散点图

scatterplot(价格~排量|性能,
              lwd=2,
              boxplots=FALSE,
              log='y',
              col=brewer.pal(2,'Set2')[c(2:1)],
              main='分组散点图'
              )

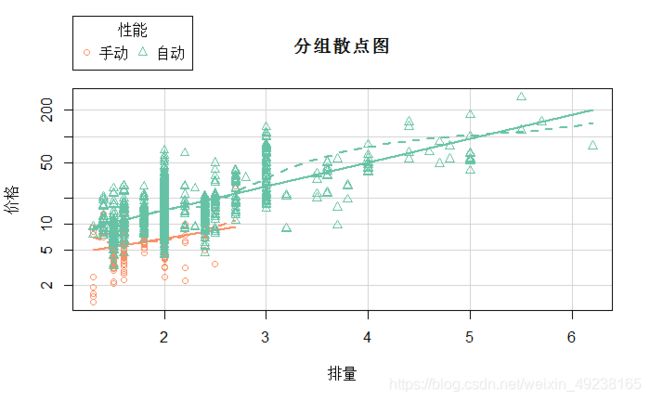
可以看出手动挡的排量和价格都相对集中在较低分段，自动挡汽车占大多数，这样的散点图传递的信息就比较丰富，如果我们现在想要所有数值型变量两两之间的散点图，那么我们可以考虑用散点图矩阵来呈现，函数为scatterplotMatrix，基本参数与scatterplot基本一致，利用iris鸢尾花数据集创建四个变量两两之间的散点矩阵，并且按不同的种类用 不同的颜色表示

#利用iris数据集创建分组散点图矩阵
scatterplotMatrix(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width|Species,
                  data=iris,
                  col=brewer.pal(3,'Set2'))

散点图矩阵是一个对称的矩阵，所以我们只观察一半的图形即可。第m行的对角线是第m个变量的分布，上有变量名称，而m行n列是第m个变量和第n个变量之间的散点图。可以看到三种不同的鸢尾花花萼花瓣长度宽度都有显著差异，比如对于最右下角的Petal.Width的分布，蓝色代表的花宽度分布相对较宽，而绿色代表的花就相对较窄。而两两之间的散点也可以看出大致上所有变量之间都是有一定的正相关性，也可以具体地再去观察所有散点图进行解读。

4. 相关图

相关系数矩阵是描述数值型变量之间相关性的方法。摘录一些R语言实战的文字

哪些被考察的变量与其他变量相关性很强，而哪些并不强？相关变量是否以某种特定的方式聚集在一起？随着变量数的增加，这类问题将变得更难回答。
相关图作为一种相对现代的方法，可通过对相关系数矩阵的可视化来回答这些问题。相关图非常容易看懂。

我们可以用corrgram包的函数corrgram()用来绘制相关图

corrgram(x, type = NULL, order = FALSE, labels, panel = panel.shade,
  lower.panel = panel, upper.panel = panel, diag.panel = NULL,
  text.panel = textPanel, label.pos = c(0.5, 0.5), label.srt = 0,
  cex.labels = NULL, font.labels = 1, row1attop = TRUE, dir = "",
  gap = 0, abs = FALSE, col.regions = colorRampPalette(c("red", "salmon",
  "white", "royalblue", "navy")), cor.method = "pearson",
  outer.labels = NULL, ...)

• order：默认FALSE，TRUE表示相关矩阵将用主成分法对变量进行重新排列，是一种很不错的重排列方法
• lower.panel：控制左下三角格子的形式，可以是饼图可以是矩形等
• upper.panel：控制右上三角格子的形式
• diag.panel：控制对角线格子的形式
• cor.method：控制计算相关系数的方法，默认皮尔森相关系数
• col.regions：控制颜色

因为相关图需要计算相关系数，故而只能对数值型变量进行操作，对于定性变量多的数据集，呈现的信息就不是很完整。所以需要选择数值型变量多的数据集，下面我们也用mtcars 数据框中的变量相关性为例，它含有11个变量，对每个变量都测量了32辆汽车。先展示相关系数矩阵的一部分：

cor(mtcars)
            mpg        cyl       disp         hp        drat         wt        qsec         vs          am
mpg   1.0000000 -0.8521620 -0.8475514 -0.7761684  0.68117191 -0.8676594  0.41868403  0.6640389  0.59983243
cyl  -0.8521620  1.0000000  0.9020329  0.8324475 -0.69993811  0.7824958 -0.59124207 -0.8108118 -0.52260705
disp -0.8475514  0.9020329  1.0000000  0.7909486 -0.71021393  0.8879799 -0.43369788 -0.7104159 -0.59122704
hp   -0.7761684  0.8324475  0.7909486  1.0000000 -0.44875912  0.6587479 -0.70822339 -0.7230967 -0.24320426
drat  0.6811719 -0.6999381 -0.7102139 -0.4487591  1.00000000 -0.7124406  0.09120476  0.4402785  0.71271113
wt   -0.8676594  0.7824958  0.8879799  0.6587479 -0.71244065  1.0000000 -0.17471588 -0.5549157 -0.69249526
qsec  0.4186840 -0.5912421 -0.4336979 -0.7082234  0.09120476 -0.1747159  1.00000000  0.7445354 -0.22986086
vs    0.6640389 -0.8108118 -0.7104159 -0.7230967  0.44027846 -0.5549157  0.74453544  1.0000000  0.16834512
am    0.5998324 -0.5226070 -0.5912270 -0.2432043  0.71271113 -0.6924953 -0.22986086  0.1683451  1.00000000
gear  0.4802848 -0.4926866 -0.5555692 -0.1257043  0.69961013 -0.5832870 -0.21268223  0.2060233  0.79405876
carb -0.5509251  0.5269883  0.3949769  0.7498125 -0.09078980  0.4276059 -0.65624923 -0.5696071  0.05753435
  

可以看出相关系数矩阵数值非常多，并且对于这些0-1之间的数字，很多时候我们难以区分到底哪些比较大，信息十分庞杂，这时候一张可视化的相关图就可以很清晰地对相关性进行展示

library(corrgram)
corrgram(mtcars,
         order=TRUE,
         #设置了上半边为饼图的形式
         upper.panel = panel.pie,
         main='corrgram of varibales'
         )

我们先从下三角单元格（在主对角线下方的单元格）开始解释这幅图形。蓝色和从左下指向右上的斜杠表示单元格中的两个变量呈正相关；反过来，红色和从左上指向右的斜杠表示变量呈负相关。颜色越深，饱和度越高，说明变量相关性越大。从图中含阴影的单元格中可以看到， gear 、 am 、 drat 和 mpg 相互间呈正相关， wt 、 disp 、hp 和 carb 相互间也呈正相关。但第一组变量和第二组变量呈负相关。正相关性将从12点钟处开始顺时针填充饼图，而负相关性则逆时针方向填充饼图，相关性越大面积越大。我们可以看出相关图矩阵可以很直观地去表现一组数值型变量的相关性，这样的图形就达到了描述性分析的目的，简约而又直接地传达信息。

基本图形就介绍到这了，很多时候在描述性分析的时候，选择合适的图形比调整视觉感受重要的多，这里又得重提一开始就说到的两个问题，如何选择合适的图？先确定要研究定性变量或是定量变量，再看是单变量还是多变量，确定这两件事，就可以找到对应的图形。除此之外R语言的ggplot2包也非常强大，通过图层叠加的方式使得绘图的逻辑更加清晰，而且画出来的图都是简约商务风的感觉，关于这个包有空再开文聊一聊，但基本的绘图以上的函数就已经可以满足大多需求了。