Bias-Variance

knitr::opts_chunk$set(echo = TRUE)

看了蛮久的，各种各样的说法，把不同的阐述分别写下，以供自己参考

Hastie-《统计学习导论 》

《ISLR》是Hastie写的基于R的统计学习教材，网上有英文版本可以免费下载，简单总结其观点。
林轩田的《ML Foundation》中提到过NFL定理(No Free Lunch)，即没有任何一种方法/模型能在各种数据集里完胜其他所有方法，ISLR也有提及。所以在面对一个具体问题时，要评价模型是否合适，理论上评价模型的指标是期望泛化误差，由于未知数据集不能获取，所以从已知数据集中抽取部分数据作为测试集，用测试误差评价模型。下面以回归问题为例：

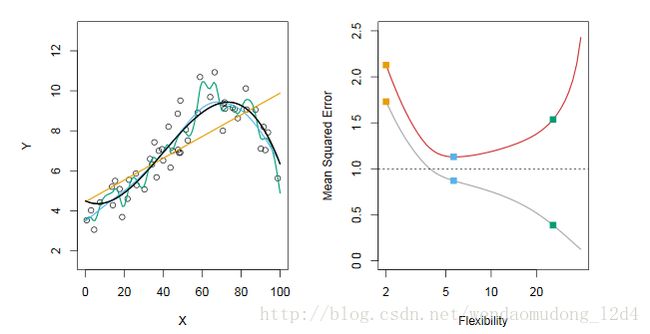
左图中，黑色曲线为真实的 f f ，橙、蓝、绿表示三种可能的对 f f 的估计；右图中是三种估计的误差，其中灰色曲线为训练均方误差，红色为测试均方误差。
从图中，可以清晰地看出随着自由度(Flexibility)的增加，这里的自由度和林轩田所说的VC维或者模型复杂度或者参数个数有一定相关性。总之，随着自由度的增加，训练误差会降低，但是测试误差会增加，即很难同时降低。
假定测试数据是一个定值 x0 x 0 ，那么期望测试均方误差可以分解成三项之和，分别为 f^(x0) f ^ ( x 0 ) 的方差、 f^(x0) f ^ ( x 0 ) 偏差的平方和误差项 ε ε 的方差，具体而言：

E(y0−f^(x0))2=Var(f^(x0))+[Bias(f^(x0))]2+Var(ε) E ( y 0 − f ^ ( x 0 ) ) 2 = V a r ( f ^ ( x 0 ) ) + [ B i a s ( f ^ ( x 0 ) ) ] 2 + V a r ( ε )

证明暂且不看，稍后再说。对于上式中期望测试均方误差，随机变量是 f^ f ^ ，不同的训练集可以训练出不同的 f^ f ^ 。
1. 方差
  对于同一个测试样本 x0 x 0 ，方差表示用一个不同的训练数据集估计 f f 时，估计函数的改变量。理想状况下，不同训练集估计得到的 f^ f ^ 应该变化不大。如果一个模型有较大的方差，那么训练集微小的变化会导致 f^ f ^ 较大的改变。一般光滑度(模型复杂度，原文是flexible)越高，模型方差越高。如图Fig1中，橙色最小二乘线复杂度不高，当移动某个观测值只会引起拟合线位置的少许变化.
2. 偏差
  偏差指模型预测值的期望与真实值的差，即 E(y0−f^(x0)) E ( y 0 − f ^ ( x 0 ) ) ，偏差反应的是模型本身的学习能力。

林轩田-《机器学习基石》

  《ML Founation》中讲learning可行的条件如下：
1. Etest≈Etrain E t e s t ≈ E t r a i n
2. Etrain≈0 E t r a i n ≈ 0
其中 Etest≈Etrain E t e s t ≈ E t r a i n 需要hypothesis set的大小有限，从而演算法可以从中挑选一个 Etrain≈0 E t r a i n ≈ 0 的 g g ，虽然这里讲的是分类模型，但是可以对照看《ISLR》的内容：

• hypothesis set的大小有限—>复杂度不是很高
• 算法挑选 g g —>训练集训练模型

可以这样看方差：
如果hypothesis set也就是模型本身，注意这里的模型本身不是训练集产生的结果，训练集产生的结果只是模型的估计，也就是说如果模型方差大，就很难做到 Etest≈Etrain E t e s t ≈ E t r a i n ，即使训练上表现很好，在测试集也未必很好，因为不满足 Etest≈Etrain E t e s t ≈ E t r a i n ，也就是所谓的过拟合。

可以这样看偏差：

偏差反应的是预测值的期望和真实值的差，如果模型方差较小，并且模型本身学习能力有限，那么演算法不能够找到合适 g g 使得 Etrain≈0 E t r a i n ≈ 0 ，此时就是所谓的欠拟合。

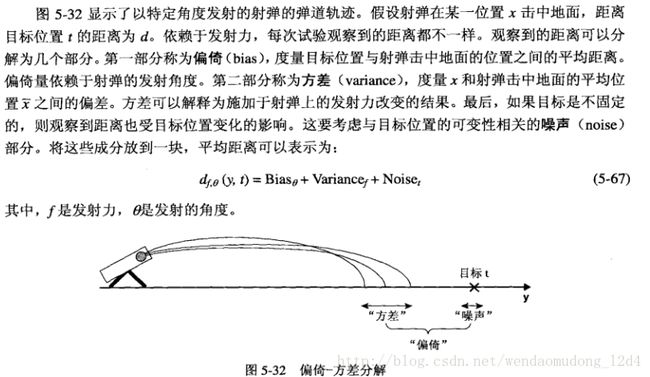
Pang-Ning Tan-《数据挖掘导论》

  这本书用了大炮的例子做了比喻，具体如下：

书上并没有严格对应到训练集、模型等，我来做个尝试：
1. 训练集—>对应每次测量大炮到目标的距离等等，类似打炮的准备工作
2. f^ f ^ —>针对训练集(真实环境)调整的打炮角度
3. 模型的稳定性—>发射力稳定性，就是文中说的发射力
4. hypothesis set—>炮的集合
要想击中目标，则需要：
1. 发射力变动小，同一个角度炮弹比较集中
2. 角度对，击中目标概率大
3. 噪声看成风向、湿度之类的影响

上面的解释比较牵强，网上有个射击的比喻:

• 模型—>射击学习者
• D1,D2…DN—>N个独立的训练计划

如果一个学习者是正常人，一个眼睛斜视，则可以想见，斜视者无论参加多少训练计划，都不会打中靶心，问题不在训练计划够不够好，而在他的先天缺陷。这就是模型偏差产生的原因，学习能力不够。正常人参加N个训练计划后，虽然也不能保证打中靶心，但随着N的增大，会越来越接近靶心。

假设还有一个超级学习者，他的学习能力特别强，参加训练计划D1时，他不仅学会了瞄准靶心，还敏感地捕捉到了训练时的风速，光线，并据此调整了瞄准的方向，此时，他的训练成绩会很好。

但是，当参加测试时的光线，风速肯定与他训练时是不一样的，他仍然按照训练时学来的瞄准方法去打靶，肯定是打不好。这样产生的误差就是方差。这叫做聪明反被聪明误。

周志华-《机器学习》

  这本书里讲了期望泛化误差分解的公式，符号标记如下：
x x :测试样本
yD y D :数据集中的标记，测试集数据下标是训练集，什么鬼
y y :测试样本的真实值，受噪声影响可能不等于 yD y D
f(x;D) f ( x ; D ) :在训练集 D D 上学得的模型 f f 在 x x 上的预测输出，注意这里的 f f 是依赖与学习模型和训练集的
以回归任务为例,叙述相关定义。

学习模型的期望预测

这里期望所对应的随机变量是 f f (吐槽这个符号标记真是不合理)，对于不同训练集，学得模型可能为 f1,f2,...fn f 1 , f 2 , . . . f n ，这些模型对样本 x x 的预测值的均值就是所谓的期望。或者可以理解成 f1,f2,...fn f 1 , f 2 , . . . f n 是对真正的 F F 的估计。

f¯(x)=ED(f(x;D)) f ¯ ( x ) = E D ( f ( x ; D ) )

方差

方差理解为样本数相同的不同训练集产生的方差，即反应的是模型的稳定性。

var(x)=ED[(f(x;D)−f¯(x))2] v a r ( x ) = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ]

偏差

期望输出与真实标记的差别

bias2(x)=(f¯(x)−y)2 b i a s 2 ( x ) = ( f ¯ ( x ) − y ) 2

噪声

方便讨论，假定噪声期望为0，即 ED(y−yD)=0 E D ( y − y D ) = 0

期望泛化误差分解

在回归中，这里的泛化误差就是 MSE M S E

E(f;D)=ED[(f(x;D)−yD)2]=ED[(f(x;D)−f¯(x)+f¯(x)−yD)2]=ED[(f(x;D)−f¯(x))2]+ED[(f¯(x)−yD)2]+ED[2(f(x;D)−f¯(x))(f¯(x)−yD)] E ( f ; D ) = E D [ ( f ( x ; D ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ¯ ( x ) + f ¯ ( x ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ] + E D [ ( f ¯ ( x ) − y D ) 2 ] + E D [ 2 ( f ( x ; D ) − f ¯ ( x ) ) ( f ¯ ( x ) − y D ) ]

最后一项可以化简：

ED[2(f(x;D)−f¯(x))(f¯(x)−yD)]=2ED(f(x;D)−f¯(x))ED(f¯(x)−yD)=2(ED[f(x;D)−f¯(x)])(ED(f¯(x)−yD))=2([ED(f(x;D))−ED(f¯(x))])(ED(f¯(x)−yD))=2(f¯(x)−f¯(x))(ED(f¯(x)−yD))=0 E D [ 2 ( f ( x ; D ) − f ¯ ( x ) ) ( f ¯ ( x ) − y D ) ] = 2 E D ( f ( x ; D ) − f ¯ ( x ) ) E D ( f ¯ ( x ) − y D ) = 2 ( E D [ f ( x ; D ) − f ¯ ( x ) ] ) ( E D ( f ¯ ( x ) − y D ) ) = 2 ( [ E D ( f ( x ; D ) ) − E D ( f ¯ ( x ) ) ] ) ( E D ( f ¯ ( x ) − y D ) ) = 2 ( f ¯ ( x ) − f ¯ ( x ) ) ( E D ( f ¯ ( x ) − y D ) ) = 0

继而

=ED[(f(x;D)−f¯(x))2]+ED[(f¯(x)−yD)2]=ED[(f(x;D)−f¯(x))2]+ED[(f¯(x)−y+y−yD)2]=ED[(f(x;D)−f¯(x))2]+ED[(f¯(x)−y)2]+ED[(y−yD)2]+2ED[(f¯(x)−y)(y−yD)] = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ] + E D [ ( f ¯ ( x ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ] + E D [ ( f ¯ ( x ) − y + y − y D ) 2 ] = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ] + E D [ ( f ¯ ( x ) − y ) 2 ] + E D [ ( y − y D ) 2 ] + 2 E D [ ( f ¯ ( x ) − y ) ( y − y D ) ]

最后一项噪声期望为0，所以 ED[(f¯(x)−y)(y−yD)] E D [ ( f ¯ ( x ) − y ) ( y − y D ) ] 为0，第二项都是常数，所以期望可以去掉

=ED[(f(x;D)−f¯(x))2]+(f¯(x)−y)2+ED[(y−yD)2]=var(x)+bias2(x)+ε2 = E D [ ( f ( x ; D ) − f ¯ ( x ) ) 2 ] + ( f ¯ ( x ) − y ) 2 + E D [ ( y − y D ) 2 ] = v a r ( x ) + b i a s 2 ( x ) + ε 2

Summary

• 偏差度量了学习算法的期望预测与真实结果的偏离程度，刻画了学习算法本身的拟合能力
• 方差度量了同样大小的训练集的变动所导致学习性能的变化，刻画了数据扰动所造成的影响，也就是模型的鲁棒性
• 噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度
  偏差-方差分解说明泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则要使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

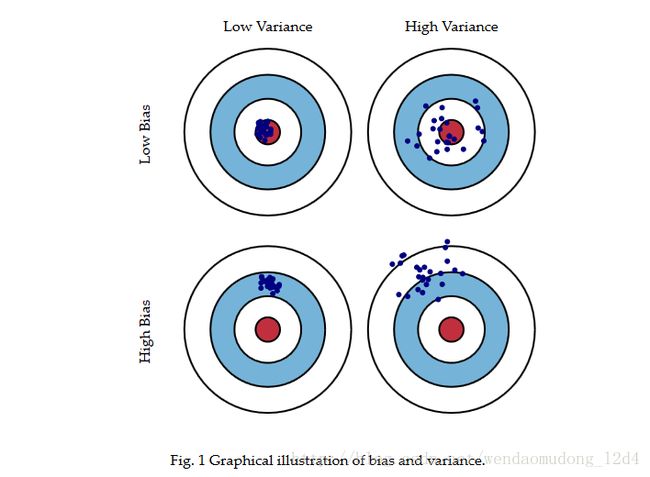
下图展示偏差-方差的四种组合情况：

如果出现高偏差情况，说明模型学习能力有限，则需要
1. 增加模型复杂度
2. 增加训练时间
如果出现高方差情况，说明模型不稳定，则需要：
1. 更多训练数据
2. 正则化，控制模型的复杂度

Ref

[1] 《机器学习》周志华
[2] 《ML Foundation》 林轩田
[3] 《数据挖掘导论》 Pang-Ning Tan
[4] 《统计学习导论》 Hastie
[5] 机器学习面试之偏差方差

                                             2018-03-10 于杭州