卷积神经网络CNN与LeNet5详解(可训练参数量、计算量、连接数的计算+项目实战)
文章目录
- 神经网络
- CNN卷积神经网络
- CNN的由来
- 局部感受野
- 共享权重
- 池化
- CNN的结构
- 光栅化
- LeNet5详解
- LeNet5-C1层
- LeNet5-S2层
- LeNet5-C3层
- LeNet5-S4层
- LeNet5-C5层
- LeNet5-F6层
- LeNet5-OUTPUT层
- 计算公式
- LeNet5实战
- 定义网络模型
- 初始化模型参数
- 训练
- 测试准确率
- 预测结果
神经网络
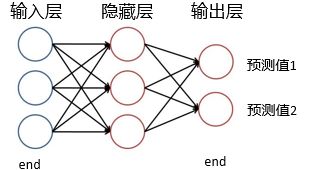
神经网络可以看成一个端到端的黑盒,中间是隐藏层(可以很深),两边是输入与输出层,完整的神经网络学习过程如下:
- 定义网络结构(指定输入层、隐藏层、输出层的大小)
- 初始化模型参数
- 循环操作:
3.1. 执行前向传播(输入参数,计算一个个结点的值得到y’,即预测值)
3.2. 计算损失函数(拿y’-y计算Loss)
3.3. 执行后向传播(求梯度,为了更新参数)
3.4. 权值更新
CNN卷积神经网络
CNN的由来
卷积神经网络(CNN)是人工神经网络的一种,是多层感知机(MLP)的一个变种模型,它是从生物学概念中演化而来的。
Hubel和Wiesel早期对猫的视觉皮层的研究中得知在视觉皮层存在一种细胞的复杂分布,这些细胞对于外界的输入局部是很敏感的,它们被称为“感受野”(细胞),它们以某种方法来覆盖整个视觉域。这些细胞就像一些滤波器一样,够更好地挖掘出自然图像中的目标的空间关系信息。
视觉皮层存在两类相关的细胞,S细胞(Simple Cell)和C(Complex Cell)细胞。S细胞在自身的感受野内最大限度地对图像中类似边缘模式的刺激做出响应,而C细胞具有更大的感受野,它可以对图像中产生刺激的模式的空间位置进行精准地定位。
卷积神经网络已成为语音和图像识别的研究热点,80年代末,Yann LeCun就作为贝尔实验室的研究员提出了卷积网络技术,并展示如何使用它来大幅度提高手写识别能力。在图像识别领域,CNN已经成为一种高效的识别方法
CNN的应用广泛,包括图像分类,目标检测,目标识别,目标跟踪,文本检测和识别以及位置估计等。
CNN的基本概念:
- 局部感受野(local receptive fields)
- 共享权重(shared weights)
- 池化(pooling)
局部感受野
局部感受野(local receptive fields):图像的空间联系是局部的,就像人通过局部的感受野去感受外界图像一样,每个神经元只感受局部的图像区域,然后在更高层,将这些感受不同局部的神经元综合起来就可以得到全局的信息了。
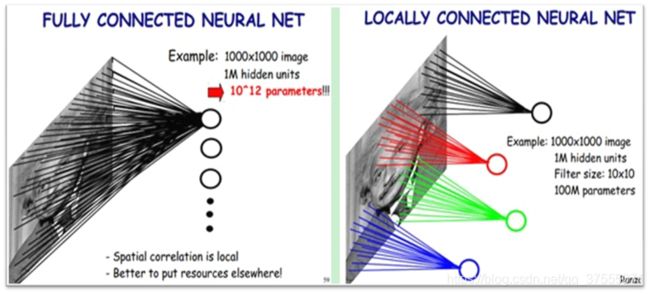
CNN中相邻层之间是部分连接,即某个神经单元的感知区域来自于上层的部分神经单元。这个与MLP多层感知机不同,MLP是全连接,某个神经单元的感知区域来自于上层的所有神经单元。
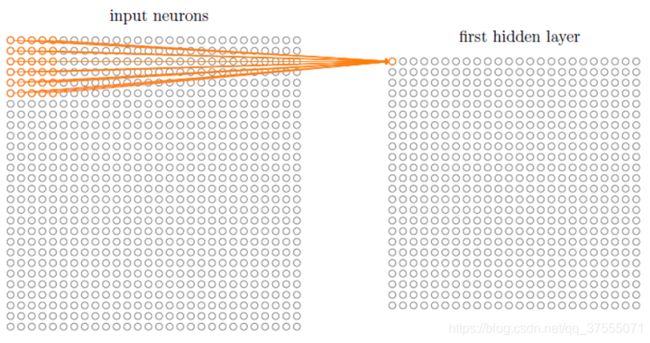
共享权重
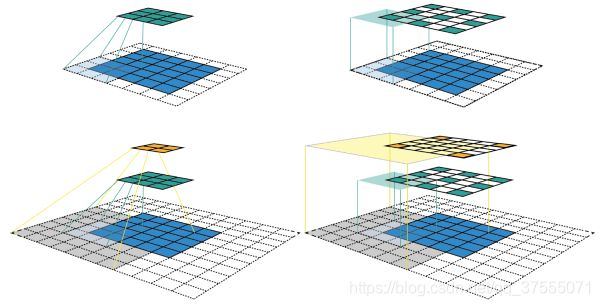
共享权重(shared weights):共享权重即参数共享,隐藏层的参数个数和隐藏层的神经元个数无关,只和滤波器的大小和滤波器种类的多少有关。也就是说,对于一个特征图,它的每一部分的卷积核的参数都是一样的。
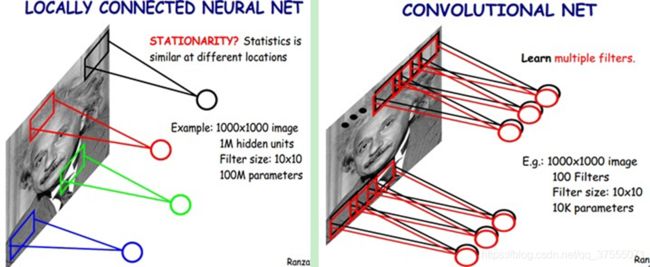
左图是没有参数共享的情况,右图进行了参数共享
如果要提取不同的特征,就需要多个滤波器。每种滤波器的参数不一样,表示它提出输入图像的不同特征。这样每种滤波器进行卷积图像就得到对图像的不同特征的反映,我们称之为Feature Map;100种卷积核就有100个Feature Map,这100个Feature Map就组成了一层神经元。
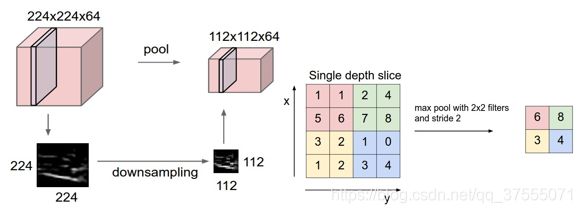
池化
池化(pooling)原理:根据图像局部相关的原理,图像某个邻域内只需要一个像素点就能表达整个区域的信息, 池化也称为混合、下采样,目的是减少参数量。分为最大池化,最小池化,平均池化。
CNN的结构
CNN的网络结构如下:
- 输入层,Input,输入可以是灰度图像或RGB彩色图像(三通道)。对于输入的图像像素分量为 [0, 255],为了计算方便一般需要归一化(如果使用sigmoid激活函数,会归一化到[0, 1],如果使用tanh激活函数,则归一化到[-1, 1])
- 卷积层,C*,特征提取层,得到特征图,目的是使原信号特征增强,并且降低噪音;
- 池化层,S*,特征映射层,将C*层多个像素变为一个像素,目的是在保留有用信息的同时,尽可能减少数据量
- 光栅化:为了与传统的多层感知器MLP全连接,就是把池化层得到的特征图拉平
- 多层感知器(MLP):最后一层为分类器,多分类使用Softmax,二分类可以使用Logistic Regression
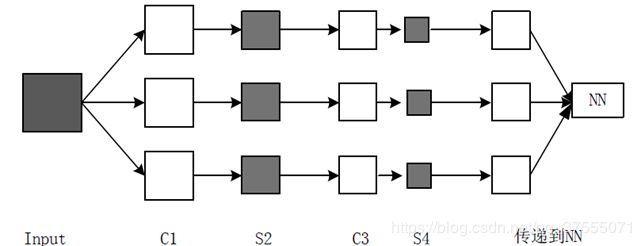
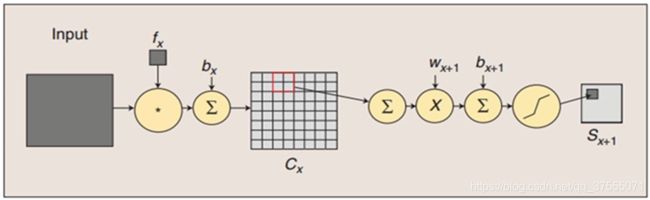
卷积过程包括:用一个可训练的滤波器fx去卷积一个输入的图像(第一阶段是输入的图像,后面的阶段就是卷积特征图),然后加一个偏置bx,得到卷积层Cx
下采样(池化)过程包括:每邻域四个像素求和变为一个像素,然后通过标量Wx+1加权,再增加偏置bx+1,然后通过一个sigmoid激活函数,产生一个缩小四倍的特征映射图Sx+1。(下图很重要,下面可训练参数量的计算就可以从这里看出)
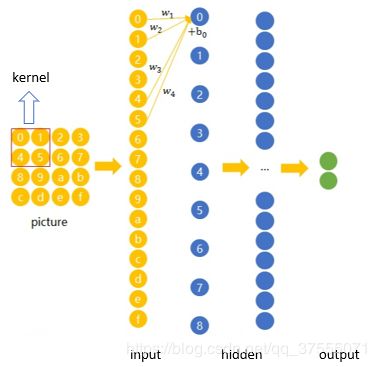
卷积神经网络就是让权重在不同位置共享的神经网络,在下图中,局部区域圈起来的所有节点会被连接到下一层的一个节点上(卷积核,称为 kernel 或 filter 或 feature detector,filter的范围叫做filter size,比如 2x2的卷积核)
上图的运算过程可用如下公式表示(上图有重要作用,下面的连接数和神经元个数就可以从这里看出来):
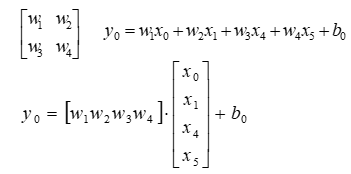
CNN学习可以帮我们进行特征提取,比如我们想要区分人脸和狗头,那么通过CNN学习,背景部位的激活度基本很少。
CNN layer越多,学习到的特征越高阶,如下图所示: - layer 1、layer 2学习到的特征基本上是颜色、边缘等低层特征
- layer 3开始稍微变得复杂,学习到的是纹理特征,比如网格纹理
- layer 4学习到的是比较有区别性的特征,比如狗头
- layer 5学习到的则是完整的,具有辨别性关键特征

光栅化
光栅化(Rasterization):为了与传统的MLP(多层感知机)全连接,把上一层的所有Feature Map的每个像素依次展开,排成一列。
图像经过下采样后,得到的是一系列的特征图,而多层感知器接受的输入是一个向量,所以需要将这些特征图中的像素依次取出,排列成一个向量。
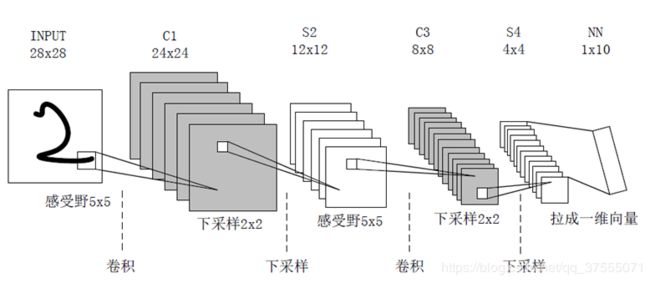
LeNet5详解
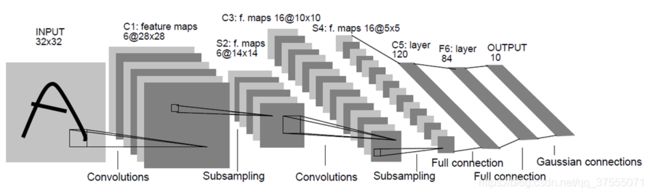
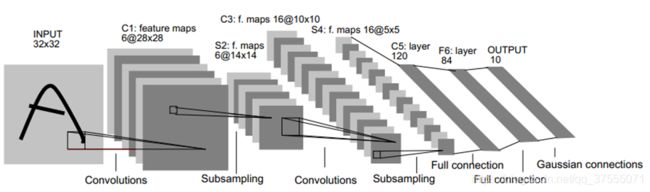
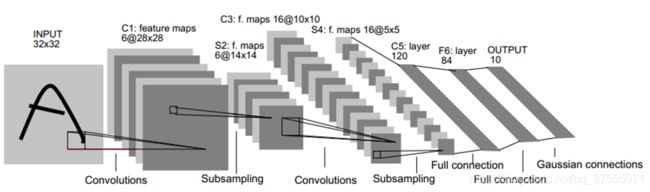
1990年,LeCun发表了一篇奠定现在CNN结构的重要文章,他们构建了一个叫做LeNet-5的多层前馈神经网络,并将其用于手写体识别。就像其他前馈神经网络,它也可以使用反向传播算法来训练。它之所以有效,是因为它能从原始图像学习到有效的特征,几乎不用对图像进行预处理。
LeNet5-C1层
LeNet5的第一层是卷积层
- 输入图片大小:
32*32 - 卷积窗大小:
5*5(作者定义) - 卷积窗种类:
6(作者定义) - 输出特征图数量:
6。
由于卷积窗种类是6,故输出的输出特征图数量也是6 - 输出特征图大小:
(32-5+1)*(32-5+1)=28*28
输出特征图大小计算可参考神经网络之多维卷积的那些事中的特征图大小计算方式 - 可训练参数量:
(5*5+1)*6或(5*5)*6+6
参数量就是卷积核中元素的个数+偏置bias,总共6种卷积核 - 计算量:
(5*5+1)*6*28*28
每一个像素的计算量是(5*5+1),总共6*28*28个像素,所以总的计算量是(5*5+1)*6*28*28 - 神经元数量:
(28*28)*6)
参考上面卷积的计算方式和图像就可以看出,计算出的一个结果(像素点)就是一个神经元 - 连接数:
(5*5+1)*6*28*28
参考上面卷积的计算方式和图像就可以看出,输入特征图的每个像素是一个神经元,输出特征图的每个像素也是一个神经元,只要参与了计算,两个神经元之间就算做一个连接,因此卷积中连接数与计算数是一样的
LeNet5-S2层
- 输入大小:
(28*28)*6 - 采样区域(池化核大小):
2*2(作者定义) - 下采样数量:
6
这6个下采样的方式其实是一样的 - 输出特征图大小:
14*14
输出特征图大小计算可参考神经网络之多维卷积的那些事中的特征图大小计算方式,卷积和池化输出特征图大小的计算方式是通用的 - 可训练参数量:
(1+1)*6
池化层的可训练参数量不是池化核元素的个数,而是每一个池化都有一个权重w和偏置b,总共6个下采样,故可训练参数是(1+1)*6 - 计算量 :
(2*2+1)*14*14*6
对于池化层的计算量,可能不同地方的描述不一样,我的理解是,采样区域是2*2,要找到最大的采样点,需要比较3次,也就是3次计算,才能找到最大值(如果采样区域是3*3,那么需要比较8次才能找到最大值),然后这个最大值再乘以权重w,加上偏置b,因此得到一个像素点的计算量是3+1+1=(2*2-1+1+1)=(2*2+1),总共14*14*6个像素点,可得总共的计算量为(2*2+1)*14*14*6 - 神经元数量:
(14*14)*6
计算出的一个结果(像素点)就是一个神经元 - 连接数:
(2*2+1)*[(14*14)*6]
每四个输入的像素点(输入四个神经元),输出的像素点为1个(输出一个神经元),再加上一个偏置的点(偏置神经元),可得每计算一个像素点的连接数是(2*2+1),总共(14*14)*6个像素点,故总的连接数为(2*2+1)*[(14*14)*6],可以看到,池化中计算量和连接数也是一样的
LeNet5-C3层
- 输入图片大小:
(14*14)*6 - 卷积窗大小:
5*5(作者定义) - 卷积窗种类:
16(作者定义) - 输出特征图数量:
16 - 输出特征图大小:
(14-5+1)*(14-5+1)=10*10 - 可训练参数量:
(6*5*5+1)*16
每张图片的输入通道是6,我们需要用对应维度的卷积核做卷积运算,也就是要用6*5*5的卷积做运算,输出通道是16,因此要有16个这样的卷积核,每个卷积核再加上一个偏置bias,所以参数量是(6*5*5+1)*16,可参考神经网络之多维卷积的那些事 - 计算量:
(6*5*5+1)*16*10*10
一个像素点的计算量为(6*5*5+1),总的输出像素个数为16*10*10,故总的计算量为(6*5*5+1)*16*10*10,这里要注意:多维卷积计算后需要把每个卷积的计算结果相加,这个相加的结果才是一个像素点,这个计算就忽略不计了 - 神经元数量:
10*10*16
参考上面卷积的计算方式和图像就可以看出,计算出的一个结果(像素点)就是一个神经元 - 连接数:
(6*5*5+1)*16*10*10
LeNet5-S4层
LeNet5的第四层是池化层(池化核大小2*2,步长为2)
- 输入大小:
(10*10)*16 - 采样区域(池化核大小):
2*2(作者定义) - 下采样数量:
16 - 输出特征图大小:
5*5 - 可训练参数量:
(1+1)*16 - 计算量 :
(2*2+1)*5*5*16 - 神经元数量:
5*5*16 - 连接数:
(2*2+1)*5*5*16
LeNet5-C5层
- 输入图片大小:
(5*5)*16 - 卷积窗大小:
5*5(作者定义) - 卷积窗种类:
120(作者定义) - 输出特征图数量:
120 - 输出特征图大小:
(5-5+1)*(5-5+1)=1*1 - 可训练参数量:
(16*5*5+1)*120 - 计算量:
(16*5*5+1)*1*1*120 - 神经元数量:
1*1*120 - 连接数:
(16*5*5+1)*1*1*120
LeNet5-F6层
- 输入图片大小:
(1*1)*120 - 卷积窗大小:
1*1(作者定义) - 卷积窗种类:
84(作者定义) - 输出特征图数量:
84 - 输出特征图大小:
1*1 - 可训练参数量:
(120+1)*84(全连接层)
这里相当于84个线性模型,即MLP多层感知机 - 计算量:
(120+1)*84 - 神经元数量:
84 - 连接数:
(120+1)*84(全连接层)
LeNet5-OUTPUT层
LeNet5的第7层是输出层
- 输入图片大小:1*84
- 输出特征图数量:1*10
输出1000000000,则表明是数字0的分类
计算公式
卷积层:设卷积核大小为k*k,步长为1,输入特征图(输入图片)大小为n*n,输入通道是a,输出通道是b(输出通道就是卷积核的种类数)
- 输出特征图大小:
(n-k+1)*(n-k+1)=m*m - 可训练参数量:
(a*k*k+1)*b - 计算量:
(a*k*k+1)*b*m*m - 神经元数量:
m*m*b - 连接数:
(a*k*k+1)*b*m*m
卷积步长为n的输出特征图大小计算方式可参考神经网络之多维卷积的那些事
池化层:设池化核大小为k*k,步长是stride,输入特征图(输入图片)大小为n*n,输入通道是a,输出通道是a(池化层输入通道和输出通道是样的)
- 输出特征图大小: n − k s t r i d e + 1 = m \frac{ n-k}{stride} + 1=m striden−k+1=m
可参考神经网络之多维卷积的那些事中的特征图大小计算方式 - 可训练参数量:
(1+1)*a
池化层可训练的参数量和池化核大小没有关系 - 计算量:
(k*k+1)*(m*m*a) - 神经元数量:
m*m*a - 连接数:
(k*k+1)*(m*m*a)
LeNet5实战
定义网络模型
import torch
from torch import nn,optim
import torchvision
import torch.nn.functional as F
#没参数可以用nn,也可以用F,有参数的只能用nn
class LeNet5(nn.Module):
def __init__(self):
super().__init__()
#定义卷定义层卷积层,1个输入通道,6个输出通道,5*5的filter,28+2+2=32
#左右、上下填充padding
#MNIST图像大小28,LeNet大小是32
self.conv1 = nn.Conv2d(1,6,5,padding=2)
#定义第二层卷积层
self.conv2 = nn.Conv2d(6,16,5)
#定义3个全连接层
self.fc1 = nn.Linear(16*5*5,120)
self.fc2 = nn.Linear(120,84)
self.fc3 = nn.Linear(84,10)
#前向传播
def forward(self,x):
#先卷积,再调用relue激活函数,然后再最大化池化
x=F.max_pool2d(F.relu(self.conv1(x)),(2,2))
x=F.max_pool2d(F.relu(self.conv2(x)),(2,2))
#num_flat_features=16*5*5
x=x.view(-1,self.num_flat_features(x))
#第一个全连接
x=F.relu(self.fc1(x))
x=F.relu(self.fc2(x))
x=self.fc3(x)
return x
def num_flat_features(self,x):
size=x.size()[1:]
num_features=1
for s in size:
num_features=num_features*s
return num_features
初始化模型参数
import torchvision.datasets as datasets
#import torchvision.transforms as transforms
from torchvision import transforms
from torch.utils.data import DataLoader
#超参数定义
#人为定义的参数是超参数,训练的是参数
EPOCH = 10 # 训练epoch次数
BATCH_SIZE = 64 # 批训练的数量
LR = 0.001 # 学习率
#首次执行download=True,下载数据集
#mnist存在的路径一定不要出现 -.?等非法字符
train_data=datasets.MNIST(root='./dataset',train=True,transform=transforms.ToTensor(),download=False)
test_data=datasets.MNIST(root='./dataset',train=False,transform=transforms.ToTensor(),download=False)
import matplotlib.pyplot as plt
%matplotlib inline
print('训练集大小',train_data.train_data.size())
print('训练集标签个数',train_data.train_labels.size())
plt.imshow(train_data.train_data[0].numpy(),cmap='gray')
plt.show()
输出:
训练集大小 torch.Size([60000, 28, 28])
训练集标签个数 torch.Size([60000])
#如果有dataloader 的话一般都是在dataset里,dataloader和dataset 这俩一般一起用的
#使用DataLoader进行分批
#shuffle=True是设置随机数种子
train_loader=DataLoader(dataset=train_data,batch_size=BATCH_SIZE,shuffle=True)
test_loader=DataLoader(dataset=test_data,batch_size=BATCH_SIZE,shuffle=True)
#创建model
model=LeNet5()
#定义损失函数
criterion=nn.CrossEntropyLoss()
#定义优化器
optimizer=optim.Adam(model.parameters(),lr=1e-3)
#device cuda:0是指使用第一个gpu
device=torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# device=torch.device('cpu')
print(device,type(device))
model.to(device)
训练
# 训练
for epoch in range(EPOCH):
for i,data in enumerate(train_loader):
inputs,labels=data
#可能会使用GPU,注意掉就不会在gpu里运行了
inputs,labels=inputs.to(device),labels.to(device)
# print(type(inputs),inputs.size(),'\n',inputs)
#前向传播
outpus=model(inputs)
#计算损失函数
loss=criterion(outpus,labels)
#清空上一轮梯度
optimizer.zero_grad()
#反向传播
loss.backward()
#参数更新
optimizer.step()
print('epoch {} loss:{:.4f}'.format(epoch+1,loss.item()))
输出:
epoch 1 loss:0.1051
epoch 2 loss:0.0102
epoch 3 loss:0.1055
epoch 4 loss:0.0070
epoch 5 loss:0.2846
epoch 6 loss:0.1184
epoch 7 loss:0.0104
epoch 8 loss:0.0014
epoch 9 loss:0.0141
epoch 10 loss:0.0126
测试准确率
#保存训练模型
torch.save(model,'dataset/mnist_lenet.pt')
model=torch.load('dataset/mnist_lenet.pt')
#测试
"""
训练完train_datasets之后,model要来测试样本了。
在model(test_datasets)之前,需要加上model.eval().
否则的话,有输入数据,即使不训练,它也会改变权值。
"""
model.eval()
correct=0
total=0
for data in test_loader:
images,labels=data
images,labels=images.to(device),labels.to(device)
#前向传播 model(images) 和 model.forward(x)一样的
out=model(images)
"""
首先得到每行最大值所在的索引(比图第7个分类是最大值,则索引是7)
然后,与真实结果比较(如果一个样本是图片7,那么该labels是7),如果相等,则加和
"""
_,predicted=torch.max(out.data,1)
total=total+labels.size(0)
correct=correct+(predicted==labels).sum().item()
#输出测试的准确率
print('10000张测试图像 准确率:{:.4f}%'.format(100*correct/total))
输出:
10000张测试图像 准确率:98.9400%
预测结果
#记住,输入源一定要转化为torch.FloatTensor,否则无法预测,并且一定要加model.eval(),否则会更新权重
def predict_Result(img):
"""
预测结果,返回预测的值
img,numpy类型,二值图像
"""
model.eval()
img=torch.from_numpy(img).type(torch.FloatTensor).unsqueeze(0).unsqueeze(1)
img=img.to(device)
out=model(img)
_,predicted=torch.max(out.data,1)
return predicted.item()
img2=train_data.train_data[167].numpy()
plt.imshow(img2,cmap='gray')
print('预测结果:',predict_Result(img2))
输出: