图像的矩，以及利用矩求图像的重心，方向

数学中的矩

维基百科关于 Moment (mathematics) 的介绍：

In mathematics, a moment is a specific quantitative measure, used in both mechanics and statistics, of the shape of a set of points. If the points represent mass, then the zeroth moment is the total mass, the first moment divided by the total mass is the center of mass, and the second moment is the rotational inertia. If the points represent probability density, then the zeroth moment is the total probability (i.e. one), the first moment is the mean, the second central moment is the variance, the third moment is the skewness, and the fourth moment (with normalization and shift) is the kurtosis. The mathematical concept is closely related to the concept of moment in physics.For a bounded distribution of mass or probability, the collection of all the moments (of all orders, from 0 to ∞) uniquely determines the distribution.

设 X 和 Y 是随机变量，c 为常数，k 为正整数，
如果 E(|X−c|k) E ( | X − c | k ) 存在，则称 E(|X−c|k) E ( | X − c | k ) 为 X 关于点 c 的 k 阶矩。

• c = 0 时， 称为 k 阶原点矩；
• c = E(x) 时，称为 k 阶中心矩。

如果 E(|X−c1|p⋅|Y−c2|q) E ( | X − c 1 | p ⋅ | Y − c 2 | q ) 存在，则称其为 X,Y 关于 c 点 p+q 阶矩。

---

图像的矩

零阶矩：

M00=∑I∑JV(i,j) M 00 = ∑ I ∑ J V ( i , j )

这里的图像是单通道图像， V（i，j） V （ i ， j ） 表示图像在 (i,j) ( i , j ) 点上的灰度值。
我们可以发现，当图像为二值图时， M00 M 00 就是这个图像上白色区域的总和，因此， M00 M 00 可以用来求二值图像（轮廓，连通域）的面积。

一阶矩：

M10=∑I∑Ji⋅V(i,j)M01=∑I∑Jj⋅V(i,j) M 10 = ∑ I ∑ J i ⋅ V ( i , j ) M 01 = ∑ I ∑ J j ⋅ V ( i , j )

当图像为二值图时, V(i,j) V ( i , j ) 只有0（黑），1（白）两个值。 M10 M 10 就是图像上所以白色区域 x坐标值的累加。因此，一阶矩可以用来求二值图像的重心:

xc=M10M00,yc=M01M00 x c = M 10 M 00 , y c = M 01 M 00

二阶矩

M20=∑I∑Ji2⋅V(i,j)M02=∑I∑Jj2⋅V(i,j)M11=∑I∑Ji⋅j⋅V(i,j) M 20 = ∑ I ∑ J i 2 ⋅ V ( i , j ) M 02 = ∑ I ∑ J j 2 ⋅ V ( i , j ) M 11 = ∑ I ∑ J i ⋅ j ⋅ V ( i , j )

二阶矩可以用来求物体形状的方向。

θ=12fastAtan2(2b,a−c) θ = 1 2 f a s t A t a n 2 ( 2 b , a − c )

其中： a=M20M00−x2c,b=M11M00−xcyc，c=M02M00−y2c a = M 20 M 00 − x c 2 , b = M 11 M 00 − x c y c ， c = M 02 M 00 − y c 2

fastAtan2()为opencv的函数，输入向量，返回一个0-360的角度。

---

这里修改一下，我之前在看二阶矩求物体形状方向的时候，有公式是这么写的：

θ=12arctan(2ba−c) θ = 1 2 a r c t a n ( 2 b a − c )

我当时很奇怪，arctan的范围是 (−π2,π2) ( − π 2 , π 2 ) ，再除以2就只有 (−π4,π4) ( − π 4 , π 4 ) ，但是物体形状的方向肯定不止这个范围，而且我在测试的时候也感觉不对，因此就写成了上面那个用opencv函数表示的公式。
其实，这个公式是对的，只不过需要再根据分子分母的正负性来判断一下象限范围，而fastAtan2()已经加入了这个功能。
顺便说一下 math.h 中atan()求出来的是弧度，而fastAtan2()求出来的是角度。

---

利用矩求图像的重心，方向

Mat image = imread(imagename, 0);//读入灰度图
Mat binary;
//二值，椭圆是黑色的，所以反色下
threshold(image, binary, 200, 255, CV_THRESH_BINARY_INV);
Moments m = moments(binary, true);//moments()函数计算出三阶及一下的矩
Point2d center(m.m10 / m.m00, m.m01 / m.m00);//此为重心
//计算方向
double a = m.m20 / m.m00 - center.x*center.x;
double b = m.m11 / m.m00 - center.x*center.y;
double c = m.m02 / m.m00 - center.y*center.y;
double theta = fastAtan2(2*b,(a - c))/2;//此为形状的方向

图片测试：








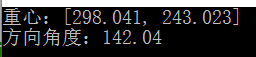
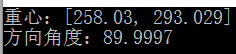
从上图可以发现，这样算出来的方向是以x轴正方向为 0 0 ，第四象限为 0−π/2 0 − π / 2 ，第三象限为 π/2−π π / 2 − π 的范围内。

---

总结

图像的矩通常描述了该图像的全局特征，并提供了大量的关于该图像不同类型的几何特性信息，比如大小，位置，方向及形状等。在模式识别，目标分类，目标识别等有着广泛的应用。