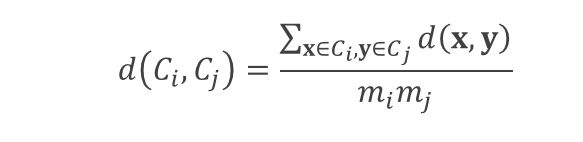机器学习之层次聚类(hierarchical clustering)
层次聚类是一组嵌套的聚类,它们被组织为树。
生成层次聚类有两种基本方法:
凝聚
分裂
在凝聚层次聚类中,我们从点作为单个聚类开始。在每一步,我们合并最近的一对集群。
这需要定义群集邻近度的概念。
在分裂的层次聚类中,我们从一个包罗万象的集群开始。在每一步,我们拆分一个集群。这个过程一直持续到只剩下单个单个点的集群。在这种情况下,我们需要做出决定在每个步骤拆分哪个集群怎么做分裂。
层次聚类通常使用树状图,以图形方式显示。
树形图显示集群 - 子集群关系和集群合并(凝聚)或分裂(分裂)的顺序。
对于2-D点集合,也可以使用嵌套聚类图以图形方式表示层次聚类。
基本的凝聚层次聚类算法总结如下:
计算邻近矩阵。重复,合并最近的两个群集,更新邻近矩阵以反映新群集与原始群集之间的接近度,直到只剩下一个集群
群集邻近度的不同定义导致不同版本的层次聚类。
这些版本包括:
单链接或MIN (Single link or MIN)
完整链接或MAX (Complete link or MAX)
Group average
Ward’s method
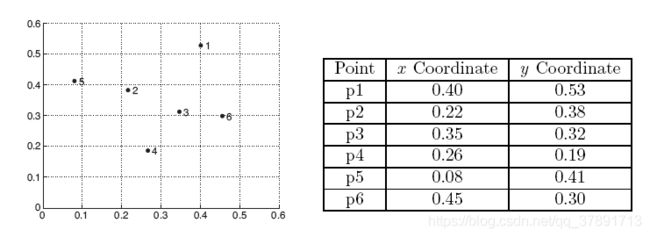
我们考虑以下数据点集。
这些数据点的欧几里德距离矩阵如下图所示。
Single link:
我们现在考虑单层链接或MIN版本的层次聚类。
在这种情况下,两个聚类的接近度被定义为两个不同聚类中任意两个点之间的距离的最小值。
该技术擅长处理非椭圆形状。但是,它对噪声和异常值很敏感。
下图显示了将单链接技术应用于示例数据的结果:

左图将嵌套簇显示为嵌套椭圆序列。
与椭圆相关联的数字表示聚类的顺序。
右图以树形图的形式显示相同的信息。
在树形图中合并两个簇的高度反映了两个簇的距离。
例如,我们看到点3和点6之间的距离是0.11。
这是它们在树形图中连接成一个簇的高度。作为另一个例子,簇{3,6}和{2,5}之间的距离是
d({3,6},{2,5})=min(d(3,2),d(6,2),d(3,5),d(6,5))
=min(0.15,0.25,0.28,0.39)
=0.15
Complete link:
我们现在考虑完整链接或MAX版本的分层聚类。
在这种情况下,两个聚类的接近度被定义为两个不同聚类中任意两个点之间的距离的最大值。
完整链接不易受噪声和异常值的影响。
但是,它倾向于产生具有球状形状的簇。
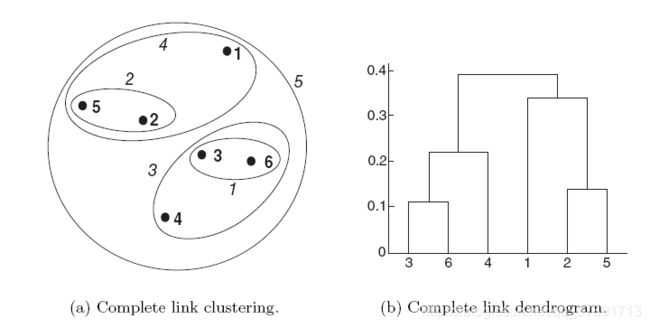
下图显示了将完整链接方法应用于我们的示例数据点的结果。
与单链路一样,第3点和第6点首先合并。
但是,{3,6}与{4}合并,而不是{2,5}或{1}。
这可以通过以下计算来解释
d({3,6},{4})=max(d(3,4),d(6,4))
=max(0.15,0.22)
=0.22
d({3,6},{2,5})=max(d(3,2),d(6,2),d(3,5),d(6,5))
=max(0.15,0.25,0.28,0.39)
=0.39
d({3,6},{1})=max(d(3,1),d(6,1))
=max(0.22,0.23)
=0.23
Group average:
我们现在考虑分层聚类的组平均版本。
在这种情况下,两个聚类的接近度被定义为不同聚类中所有点对之间的平均成对接近度。
这是单一和完整链接方法之间的中间方法。
我们考虑两个簇Ci和Cj,它们分别具有mi和mj的大小。
两个簇之间的距离可以用以下等式表示:
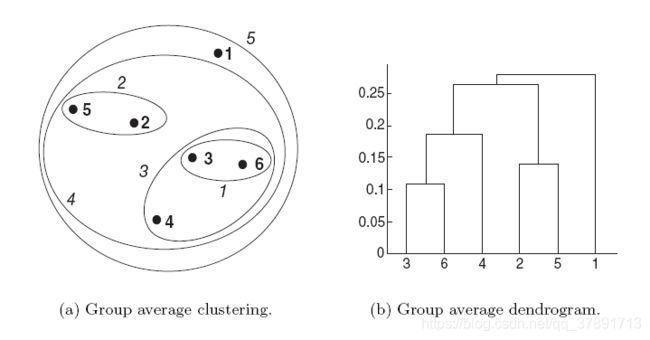
下图显示了将组平均值应用于我们的样本数据的结果。
某些群集之间的距离计算如下:
d({3,6,4},{1})=(0.22+0.37+0.23)/(3×1)= 0.27
d({2,5},{1})=(0.24+0.34)/(2×1)= 0.29
d({3,6,4},{2,5})=(0.15+0.28+ 0.25+0.39+0.20+0.29)/(3×2)= 0.26
我们观察到d({3,6,4},{2,5})小于d({3,6,4},{1})和d({2,5},{1})。
结果,{3,6,4}和{2,5}在第四阶段合并。
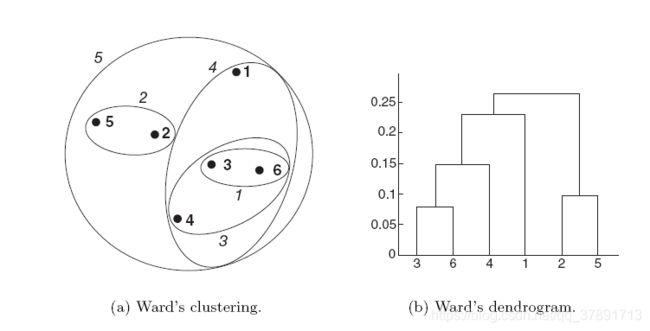
Ward’s method:
我们现在考虑Ward的层次聚类方法。
在这种情况下,两个簇之间的接近度被定义为合并时产生的平方误差之和的增加。
因此,该方法使用与k均值聚类相同的目标函数。下图显示了将Ward方法应用于我们的样本数据的结果。
产生的聚类不同于单链接,完整链接和组平均产生的聚类。
当底层应用程序需要创建多级结构时,分层聚类很有效。然而,就计算和存储要求而言,它们是昂贵的。此外,一旦决定合并两个集群,它就不能在以后撤消。