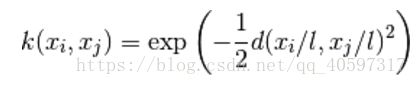python.sklearn.gaussian_process高斯过程回归的调用
代码来源:http://f.dataguru.cn/thread-878564-1-1.html(土匪加步枪)侵删
因为最近在做GPR和Bayesian optimization,需要调用python相关库,于是上网找了网友的代码参考,感谢
绿色部分为我的查阅资料内容,是对GPR相关方法的解读,可以直接当成注释看
# -*- coding: utf-8 -*-
#高斯过程回归,首先要判断,所求的是否满足正太分布,如果满足,就可以用高斯正太回归。可以参考一下代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C# REF就是高斯核函数
from mpl_toolkits.mplot3d import Axes3D#实现数据可视化3D
#创建数据集
test = np.array([[2004,98.31]])
data = np.array([
[2001,100.83,410],[2005,90.9,500],[2007,130.03,550],[2004,78.88,410],[2006,74.22,460],
[2005,90.4,497],[1983,64.59,370],[2000,164.06,610],[2003,147.5,560],[2003,58.51,408],
[1999,95.11,565],[2000,85.57,430],[1995,66.44,378],[2003,94.27,498],[2007,125.1,760],
[2006,111.2,730],[2008,88.99,430],[2005,92.13,506],[2008,101.35,405],[2000,158.9,615]])
#核函数的取值
kernel = C(0.1, (0.001,0.1))*RBF(0.5,(1e-4,10))# C(0.1, (0.001,0.1))就是sqrt(0.1)**2,我实验了一下,我们第二个参数取什么,指数上都是2?
RBF原型说明:第一个参数:length_scale(即L)float or array with shape (n_features,), default: 1.0
第二个参数:length_scale_bounds : pair of floats >= 0, default: (1e-5, 1e5):The lower and upper bound on length_scale
#创建高斯过程回归,并训练
reg = GaussianProcessRegressor(kernel=kernel,n_restarts_optimizer=10,alpha=0.1)#alpha就是添加到协方差矩阵对角线上的值,n_restarts_optimizer规定了优化过程的次数
reg.fit(data[:,:-1], data[:,-1])#这是拟合高斯过程回归的步骤,data[:,:-1]获取前两列元素值,data[:,-1]获取后两列元素的值
#创建一个作图用的网格的测试数据,数据位线性,x为【1982,2009】间隔位0.5;y为【57.5,165】间隔位0.5
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1#获取data的第一列年份的最小值减1和最大值加1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1#获取data的第二列面积的最小值减1和最大值加1
xset, yset = np.meshgrid(np.arange(x_min, x_max, 0.5), np.arange(y_min, y_max, 0.5))
#np.arange(x_min,x_max,0.5)获取x_min和x_max之间的坐闭右开的以0.5位间隔的array,meshgrid用于点的绘制,参考https://zhuanlan.zhihu.com/p/29663486(有时间写一篇单独的) ,假设x_max到x_min生成的array里面元素的个数为m,y_max到y_min生成的元素的个数为n,那么xset和yset为一个n*m的array,分别包含所有X坐标的xset,包含所有Y坐标
#查看网格测试数据输出结果,并返回标准差。
output,err = reg.predict(np.c_[xset.ravel(), yset.ravel()],return_std=True)#np.r_是按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等,类似于pandas中的concat()。
np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等,类似于pandas中的merge()。
ravel()按行优先把数组降成一维的,return_std如果为True,则查询点处的预测分布的标准偏差与平均值一起返回。默认false,返回的均值和方差还是一维的
output,err = output.reshape(xset.shape),err.reshape(xset.shape)#使均值和方差的维数与xset一致
sigma = np.sum(reg.predict(data[:,:-1], return_std=True)[1])#预测原来的给出的data在z上的数据,[1]返回方差
up,down = output*(1+1.96*err), output*(1-1.96*err)#这是置信区间95%
#作图,并画出
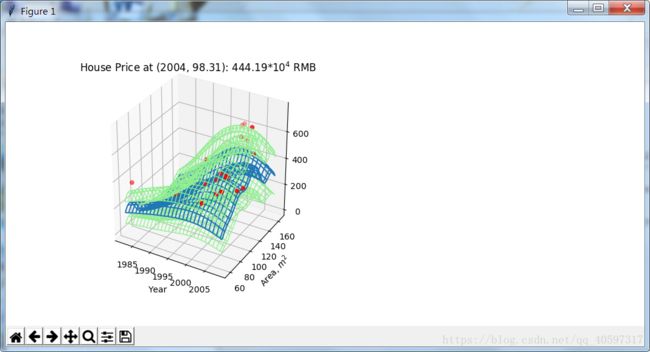
fig = plt.figure(figsize=(10.5,5))
ax1 = fig.add_subplot(121, projection='3d')#画上一个1*2的图形,在第一个位置,这就是121的含义
surf = ax1.plot_wireframe(xset,yset,output, rstride=10, cstride=2, antialiased=True)#rside,cstride分别表示数组行的步长和数组列的步长,antialiased表示抗锯齿程度,True表示尽可能使图形光滑
surf_u = ax1.plot_wireframe(xset,yset,up,colors='lightgreen',linewidths=1,
rstride=10, cstride=2, antialiased=True)#linewidth表示线宽
surf_d = ax1.plot_wireframe(xset,yset,down,colors='lightgreen',linewidths=1,
rstride=10, cstride=2, antialiased=True)
ax1.scatter(data[:,0],data[:,1],data[:,2],c='red')#scatter表示画分散的点
ax1.set_title('House Price at (2004, 98.31): {0:.2f}$*10^4$ RMB'.format(reg.predict(test)[0]))
ax1.set_xlabel('Year')
ax1.set_ylabel('Area, $m^2$')
plt.show()