【CF】Codeforces Round #515 (Div. 3)

前言

打了一场 $CF$ 的重现赛，然而发现自己连 $Div$ $3$ 都打不好…好颓呀 $QAQ$
怎么办办呢——写篇题解重温一下代码吧…
PS：题目描述都多数用中文，少数用英文，敬请谅解！

传送门

CF Round #515(Div. 3)

题目

A - Vova and Train

Description

$Vova$ 计划乘火车去参加会议。 最初，列车在点 $1$，路径的目的地点是点L.列车的速度是每分钟 $1$个长度单位（即在第一分钟，火车在第 $1$ 点，第二分钟） - 在第 $2$ 点等等）。

路上有灯笼。 它们被放置在具有可被v整除的坐标的点处（即，第一个灯点位于点 $v$，第二个点位于点$2v$，依此类推）。
还有一条直立列车占据了从l到r的所有点。
如果 $p$ 可被 $v$ 整除，并且在该位置没有站立列车（$p\notin [l;r]$），$Vova$ 可以在点 $p$ 处看到灯笼。 因此，如果带灯笼的点是站立列车所覆盖的点之一，那么 $Vova$ 就看不到这个灯笼了。
你的问题是 $Vova$ 在路径中会看到的灯笼数量。 $Vova$ 计划参加不同的会议，因此您应该回答独立的查询。

Input

输入的第一行包含一个整数 $t$（$1\le t\le 10000$） - 查询数。

然后是 $t$ 行。 第 $i$ 行包含四个整数 $Li，vi，li，ri$（$1\le L$ , $v\le 1e9$ , $1\le l\le r\le L$） - 第 $i$ 个路径的目标点，灯笼外观的周期和 站立列车占用的段。

Output

打印 $t$ 行。 第 $i$ 行应该包含一个整数 - 第 $i$ 个查询的答案。

Example

Input

4
10 2 3 7
100 51 51 51
1234 1 100 199
1000000000 1 1 1000000000

Output

3
0
1134
0

Note

对于第一个示例查询，答案是 $3$.在位置 $2,4,6,8$ 和 $10$ 处有灯笼，但由于站立列车，$Vova$ 没有看到位置 $4$ 和 $6$ 的灯笼。

对于第二个示例查询，答案是 $0$，因为唯一的灯笼位于点 $51$处，此时还有一个站立列车。

对于第三个示例查询，答案是 $1134$，因为有 $1234$ 个灯笼，但是 $Vova$ 没有看到从位置 $100$ 到位置 $199$ 的灯笼。

对于第四个示例查询，答案为 $0$，因为站立列车覆盖整个路径。

Solution

• 好像是一道数学题…显然 暴力会超时，所以怎么写来着…
• 直接做除法？突然有一个思路浮现在我的脑海里：首先算出站立列车所占位置中的灯笼数量，然后用整条路径中灯笼数量减去它，不就是可以看到的灯笼数量吗？然后就是算站立列车占的灯笼数，就等于起点到列车尾灯笼数量减去起点到(列车头-1)的灯笼数。
• 然后这道题就可以解决了

Code

#include 
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	for (int i=1;i<=t;i++)
	{
		long long end,v,left,right;
		scanf("%lld %lld %lld %lld",&end,&v,&left,&right);
		long long x;
		x=right/v-(left-1)/v;
		printf("%lld\n",end/v-x);
	}
	return 0;
}

B - Heaters

Description

张老师是我们的红太阳

有 $n$ 个位置顺序排列。张老师可以在某些位置放置他的分身。假设 $x$ 位置放置了一个张分身，这样位置在 $[x-r+1,x+r-1]$ 范围内的所有位置都可以被张老师的光辉照亮

所有位置都想要被照亮，请问张老师要至少放多少个分身？

或者无解的话输出 $-1$。

Input

输入的第一行包含两个整数 $n$ 和 $r$（$1\le n$，$r\le 1000$） - 位置的个数和张老师的加热半径。

第二行包含 $n$ 个整数 $a1$，$a2$，…，（$0\le ai\le 1$） - $a_i=1$ 代表该位置可以放张老师的分身，但不一定有必要。

Output

打印一个整数 - 张老师至少要放的分身个数，如果不可能照亮所有位置，则为-1。

Sample In 1

6 2
0 1 1 0 0 1

Sample Out 1

3

Sample In 2

5 3
1 0 0 0 1

Sample Out 2

2

Sample In 3

5 10
0 0 0 0 0

Sample Out 3

-1

Sample In 4

10 3
0 0 1 1 0 1 0 0 0 1

Sample In 4

3

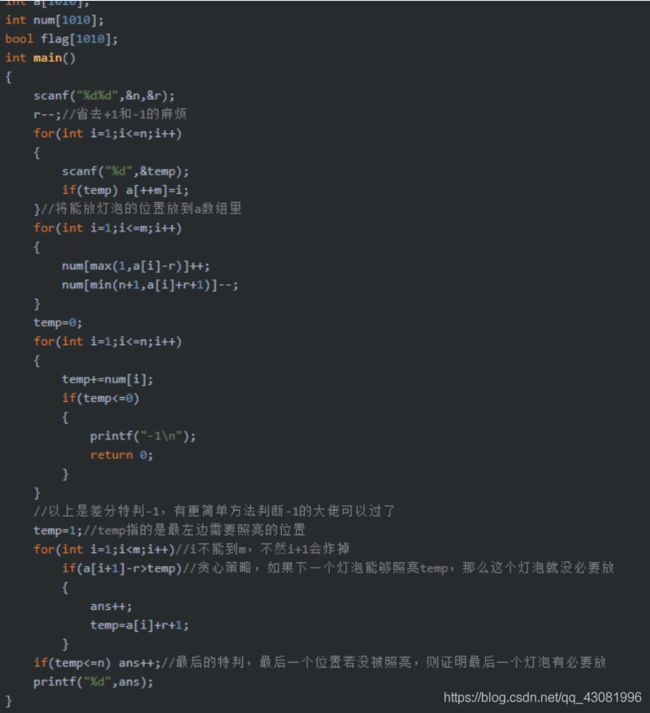
Solution

• 这道题正解是贪心，但还是有一些细节的，这里提供一个二重循环的暴力思路。
• 首先枚举每一个位置，(当然如果当前位置已经被照亮就不用进行下面的操作了)

1. 再能照亮当前点且能放置分身的点中寻找一个未使用过的点，记录位置
2. 如果找到一个可以放置分身且能照亮当前位置的点，标记数组中以灯为中心被照亮的所有点，答案+1；否则说明不合法，直接输出 -1 即可。

Code

#include 
using namespace std;
int a[1010],b[1010],f[1010];
int n,r;
int main()
{
	scanf("%d %d",&n,&r);
	memset(b,0,sizeof(b));
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	int ans=0;
	for (int i=1;i<=n;i++)
	{
		if (b[i]==0)
		{
			int x=0;
			for (int j=max(i-r+1,0);j<=i+r-1;j++)
			{
				if (a[j]==1 && !f[j])
				{
					x=j;
				}
			}
			if (x==0)
			{
				cout << -1;
				return 0;
			}
			f[x]=1;
			ans++;
			for (int j=x-r+1;j<=x+r-1;j++)
			{
				b[j]=1;
			}
		}
	}
	cout << ans;
	return 0;
}

这里提供另一种做法，就是特判-1的代码有些冗长

C - Books Queries

Description

张老师没钱恰饭了。

于是张老师来到了图书馆当管理员。

然而可恶的负责人总是用复杂的操作来刁难张老师。有三种操作：

1. L id 把一本编号为id的书放到书架的最左边。

2. R id 把一本编号为id的书放到书架的最右边。

3. ? id 询问需要从左侧或右侧弹出的最小书数，使得编号为id的书在最左侧或最右侧。

初始书架为空，3查询始终有效（保证每个此类查询中的书已经放置）并且不会将相同的书放在书架上两次。

然而负责人没想到这种难度的题对张老师来说比喝水还简单，但张老师忙着玩switch，所以只能交给你了。

请注意，3查询后，所有书籍都保留在书架上，书籍的相对顺序不会改变。

Input

输入的第一行包含一个整数q（1≤q≤200000） - 查询数。

然后是q行。 第i行包含问题语句中格式的第i个查询。 保证查询始终有效（对于查询类型3，保证每个此类查询中的书已经放置，而对于其他类型，保证之前未放置该书）。

保证输入中至少有一个类型3的查询。

在每个查询中，满足约束1≤id≤200000。

Output

对于每一个3查询，输出答案。

Sample In 1

8
L 1
R 2
R 3
? 2
L 4
? 1
L 5
? 1

Sample Out 1

1
1
2

Sample In 2

10
L 100
R 100000
R 123
L 101
? 123
L 10
R 115
? 100
R 110
? 115

Sample Out 2

0
2
1

Solution

• 乍一看：区间修改，区间查询？树状数组好哇！然而毫无头绪的我默默看着旁边HZY大佬秀树状数组…
• 然后不知怎的我就想到了双端队列：

1. 开两个指针，分别是队列的头和尾
2. 操作 ‘L’：扔到队头，记录当前编号的书放的位置 a[x]（下同）
3. 操作 ‘R’：扔到队尾
4. 操作 ‘?’：取 a[x] 距离队头和队尾两者的最小值

Code

#include 
using namespace std;
const int N=2*1e5+10;
int a[N*2];
int main()
{
	int T;
	scanf("%d",&T);
	int l=N;
	int r=l-1;
	for (int i=1;i<=T;i++)
	{
		char ch;
		int x;
		cin >> ch >> x;
		if (ch=='L')
		{
			a[x]=--l;
		}
		if (ch=='R')
		{
			a[x]=++r;
		}
		if (ch=='?')
		{
			printf("%d\n",min(a[x]-l,r-a[x]));
		}
	}
	return 0;
}

D - Boxes Packing

Description

达达小朋友拥有n个物品和m个盒子，每个盒子的大小正好是k。物品从左到右依次从1到n编号，第i个物体的大小是ai。

达达小朋友想把他的物品装进盒子里，他会用以下的算法打包物品：他拿一个空盒子，从左到右遍历物体，如果第i个物品适合当前盒子（即盒子的剩余大小大于或等于ai），他把它放在盒子里，盒子的剩余大小减少了ai。否则，他将拿新的空盒子并继续上述过程。

达达小朋友希望通过上述算法知道他可以打包的最多物品。为了达到这个目标，他可以从集合中丢弃最左边的物品，直到剩下的一组物品可以打包在他拥有的盒子中。（要保证这组物品所有都能放进盒子中）

你的任务就是计算达达小朋友可以在他所拥有的盒子里装入的最多物品数量。

Input

输入的第一行包含三个整数n，m，k（1≤n，m≤2⋅1e5,1≤k≤1e9） - 物品的数量，盒子的数量和每个盒子的大小。

输入的第二行包含n个整数a1，a2，…，a（1≤ai≤k），其中ai是第i个对象的大小。

Output

使用问题陈述中描述的算法打印达达小朋友可以打包的最大物品数。

Examples

Input
5 2 6
5 2 1 4 2
Output
4
Input
5 1 4
4 2 3 4 1
Output
1
Input
5 3 3
1 2 3 1 1
Output
5

Note

在第一个例子中，达达小朋友只能打包4个物品。 首先，他试图打包所有5个物品。 物品的分布将是[5]，[2,1]。 达达小朋友无法在第二个盒子中打包下一个物体，而且根本没有空盒子。 接下来他将抛出第一个物体，物体分布将是[2,1]，[4,2]。 所以答案是4。

在第二个例子中，很明显达达小朋友无法打包从第一，第二，第三和第四开始的所有物品（在所有这些情况下，对象的分布是[4]），但他可以打包最后一个物品（[1]）。

在第三个例子中，马克西姆可以打包他拥有的所有物品。 分布将是[1,2]，[3]，[1,1]。

Solution

• 首先，这是一道坑人的题（代码极短）【大雾】
• 根据题意，丢掉的是左边的一段，那么最后放进去的就是靠后连续的一段.
• Old Liu:“正难则反。”
• 我们直接从最后一个开始枚举，开一个变量t，表示当前盒子剩余容量：

1. 如果当前的物品大小小于等于 t，扔进去，t减去占用空间；
2. 如果当前的物品大小大于 t 且还有剩下的盒子，重开一个新的盒子，把物品丢进去；

• PS.上述二步答案都要+1
  这样一波分析后是不是感觉很简单（自己被坑了还在这瞎吹 ）？

Code

#include 
using namespace std;
const int N=2*1e5+10;
int a[N];
int main()
{
	int n,m,k;
	scanf("%d %d %d",&n,&m,&k);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	int now=k,ans=0;
	for (int i=n;i>=1;i--)
	{
		if (now>=a[i])
		{
			now-=a[i]; ans++;
		}
		else
		{
			if (--m==0) break;
			now=k-a[i]; ans++;
		}
	}
	printf("%d",ans);
	return 0;
}

E - Binary Numbers AND Sum

Description

您将获得两个长度为n和m的巨大二进制整数a和b。 您将重复以下过程：如果b> 0，则将值a和b加上答案并将b除以2舍入（即删除b的最后一位），然后再次重复该过程，否则停止该过程。

值a和b表示a和b的按位AND。 你的任务是计算答案模998244353。

请注意，您应该使用十进制表示法将值a和b添加到答案中，而不是二进制。 所以你的任务是用十进制表示法计算答案。 例如，如果a = 1010(2) =10(10)并且b = 1000(2) = 8(10)，则值a和b将等于8，而不是1000。

Input

输入的第一行包含两个整数n和m（1≤n，m≤2⋅1e5） - a的长度和b的长度。

输入的第二行包含一个巨大的整数a。 保证该数字恰好包含n个零和1，第一个数字始终为1。

输入的第三行包含一个巨大的整数b。 保证这个数字恰好是m个零和1，第一个数字总是1。

Output

以十进制表示法模数998244353打印此问题的答案。

Examples

Input
4 4
1010
1101
Output
12
Input
4 5
1001
10101
Output
11

Note

第一个例子的算法：

添加到答案1010(2)＆1101(2) = 1000(2) = 8(10)并设置b= 110(2) ;

添加到答案1010(2)＆110(2) = 10(2) = 2(10)并设置b= 11(2) ;

添加到答案1010(2)＆11(2) = 10(2) = 2(10)并设置b= 1(2) ;

添加到答案1010(2)＆1(2) = 0(2) = 0(10)并设置b= 0(2) 。

所以答案是8 + 2 + 2 + 0 = 12。

Solution

• 这道题是关于位运算的，可以想到用前缀和记录1的个数。
• 对于a来说，二进制位上，如果某一个二进制位上为0，那么肯定对结果是不会造成影响的，我们只在乎a上二进制位 为1的数字，那么假设是第 $k$ 位，每加一次，对结果造成的影响应该是 $2^{k=1}$ .
  算每次b右移的串利用的b高位的1在右移中一定会和a中比它位低的所有1与成1，所以就可以用前缀和
  计算这个位前面有多少个1，就知道这个a这个位产生了过多少次非零数，加和起来就是总数了。

Code

#include 
using namespace std;
const int Mod=998244353;
const int N=2*1e5+10;
long long a[N],b[N],f[N],s[N];
int n,m;
void binary()
{
	f[1]=1;
	for (int i=2;i<=n;i++) f[i]=f[i-1]*2%Mod;
}
int main()
{
	scanf("%d %d",&n,&m);
	binary();
	for (int i=0;i<n;i++)
	{
		char ch;
		cin >> ch;
		a[n-i]=ch-'0'; 
	}
	for (int i=0;i<m;i++)
	{
		char ch;
		cin >> ch;
		b[m-i]=ch-'0';
	}
	for (int i=max(n,m);i>=1;i--)
	{
		s[i]=s[i+1]+b[i];
	}
	long long ans=0;
	for (int i=1;i<=max(n,m);i++)
	 if (a[i]) ans=(ans+1LL*s[i]*f[i])%Mod;
	printf("%lld",ans);
	return 0;
}

F-Yet another 2D Walking

Description

Maksim walks on a Cartesian plane. Initially, he stands at the point (0,0) and in one move he can go to any of four adjacent points (left, right, up, down). For example, if Maksim is currently at the point (0,0), he can go to any of the following points in one move:

(1,0);
(0,1);
(−1,0);
(0,−1).
There are also n distinct key points at this plane. The i-th point is pi=(xi,yi). It is guaranteed that 0≤xi and 0≤yi and there is no key point (0,0).

Let the first level points be such points that max(xi,yi)=1, the second level points be such points that max(xi,yi)=2 and so on. Maksim wants to visit all the key points. But he shouldn’t visit points of level i+1 if he does not visit all the points of level i. He starts visiting the points from the minimum level of point from the given set.

The distance between two points (x1,y1) and (x2,y2) is |x1−x2|+|y1−y2| where |v| is the absolute value of v.

Maksim wants to visit all the key points in such a way that the total distance he walks will be minimum possible. Your task is to find this distance.

If you are Python programmer, consider using PyPy instead of Python when you submit your code.
中文
小M在平面直角坐标系上的 (0,0)(0,0) 点。他每次可以向上，下，左，右走一格。
坐标系上有 nn 个关键点。第 ii 个关键点的坐标为 ($x_i,y_i$) (保证 $x_i,y_i$均为非负整数，且在 (0,0) 处没有关键点) 。
设 $m_i=\max (x_i,y_i)$，那么我们称第 ii 个关键点的级别为 $m_i$ 。
现在小M想要经过所有的关键点，但是如果小M没有经过所有级别为 a 的关键点，他就不能经过级别大于 a 的关键点。
小M想知道，此时经过所有的关键点至少要走多远。两点间距离为曼哈顿距离 (即 ($x_1,y_1$)与 ($x_2,y_2$)的距离为 $|x_1-x_2|+|y_1-y_2|$ ) 。

Input

The first line of the input contains one integer n (1≤n≤2⋅105) — the number of key points.

Each of the next n lines contains two integers xi, yi (0≤xi,yi≤109) — x-coordinate of the key point pi and y-coordinate of the key point pi. It is guaranteed that all the points are distinct and the point (0,0) is not in this set.

Output

Print one integer — the minimum possible total distance Maksim has to travel if he needs to visit all key points in a way described above.

Examples

Input
8
2 2
1 4
2 3
3 1
3 4
1 1
4 3
1 2
Output
15
Input
5
2 1
1 0
2 0
3 2
0 3
Output
9

Note

The picture corresponding to the first example:

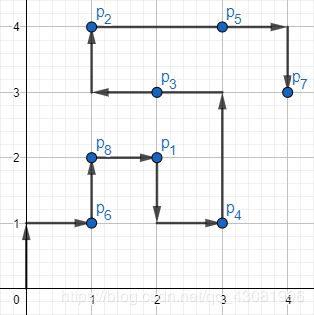
There is one of the possible answers of length 15.

The picture corresponding to the second example:

There is one of the possible answers of length 9.

备注

这里有一个题解整合版：戳这里 或者 戳这里