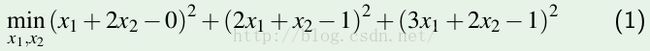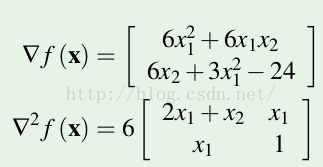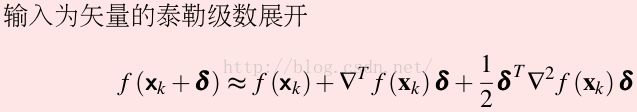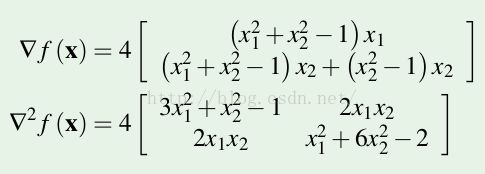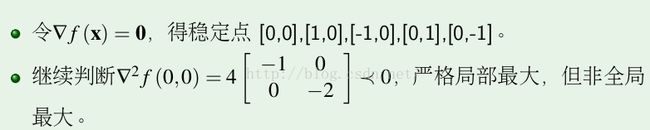七月算法机器学习笔记3--凸优化
这套笔记是跟着七月算法四月机器学习班的学习而记录的，主要记一下我再学习机器学习的时候一些概念比较模糊的地方，具体课程参考七月算法官网：
http://www.julyedu.com/1. 无约束优化问题
1.1 举例
首先看一个例子，
对于这个方程组，由于b=[0 1 1]' 不在系数组成的列空间内，即
因此，这个方程没有解。但是，是否可以找到一个近似解。即
可得：
其最小值为 0.038；
1.2 无约束优化问题
在下方平面的部分叫做等高线。表示三维空间中所有的横切面（俯视图）构成的集合。
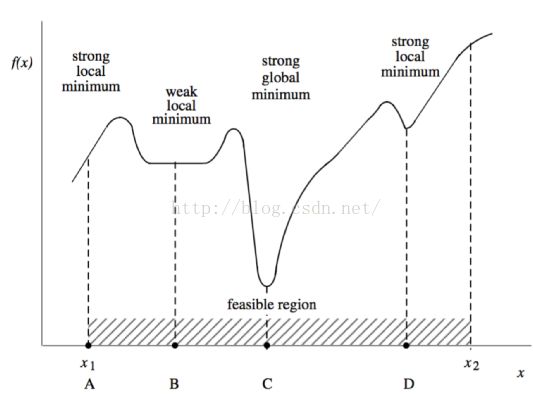
1.3优化问题中可能的极值点：
这里，C点是这个区域的最小值点，B,D为局部最小值点。A，C为局部最大值点
还有一种点，叫拐点，它的一阶导数为0，但是并非极值点。
1.4 梯度和Hessian矩阵
对函数的每一个变量求偏导数
H为一个对称矩阵。Hession矩阵的特征值大于0.
Hessian矩阵举例
对函数
求导数
1.5 泰勒级数展开（标量）
因为后面的导数比较小，可以忽略
为什么在函数可导的情况下，极值点的一阶导数一定为0？
这里，假设
取值在
的周围。上述泰勒展开式的最后一项就可以去掉。则原始变为
这时，要让
为最小值点，即
无论取正取负（简单理解就是无论在的左侧还是右侧），左式都要大于右式，这时，只有一阶导为0才能满足条件。
为什么一阶导数为0，二阶导数>0就是严格的局部极小值点？
考虑式
这里，一阶导数已经为0. 二阶导数为正，因此，左式大于（这么想，加一个正数约等于左式），相对于邻居的点最小，所以为局部最小值点。
二阶导数为0，可能为鞍点。以x^3为例， 其一阶，二阶导数均为0，则要从更高阶取判断，三阶导数不为0则其正负与的正负有关。x^3在0点是个拐点。
泰勒级数展开(矢量)
其判断与标量一致
此处的0为向量，
如果一阶梯度为0， hessian矩阵正定即为严格局部最小值。
泰勒级数矢量更高阶阶的叫张量。
1.6 级值判断举例
求导数
得到
该函数如图所示：
1.7 无约束的优化问题的局限：
a. 函数不可导；
b.可导，但是变量太多无法求解；
c. 解可能是一个集合。
1.8 无约束优化迭代法
各种迭代法最主要的不同点就是第二步，d方向的不同
1.8.1 深度下降法：
首先，d为什么取负梯度方向？
在上式中，目的要使得
比小，那么，下降最快的的方式就是使得一阶导数
与两个向量的夹角为180度（等于
），向量内积的公式|a||b|cos(t); 沿着负梯度方向下降最快。
1.8.2 牛顿法
在梯度下降法中，我们没有计算二阶导数，而在牛顿法中，加入了Hessian矩阵。
对于d的值，给出求解方法：
由于牛顿法涉及到hessian矩阵的求逆，但是Hessian未必可逆；
1.8.2 拟牛顿法
2. 有约束的优化问题
2.1 约束优化问题的一般形式：
这里，约束条件有等式，也有不等式。即要满足f(x)，也要满足约束条件。
可行域上的最优解一定会碰到一个边界。即至少有一个c (x) = 0;
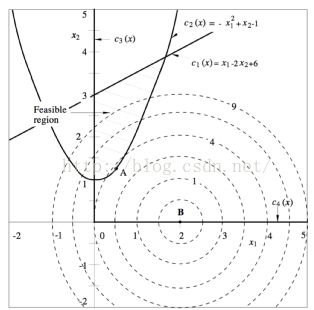
举例：
如下图：
在约束条件下，可行域围成的区间为抛物线以上，直线一下的那部分区域。最优解必须在可行域中。
最优解为A点。最优解会碰到c2边界。
2.2 KKT 一般限制优化问题极值点一阶必要条件
KKT条件可以求局部最优解，在凸函数下可以得到全局最优解
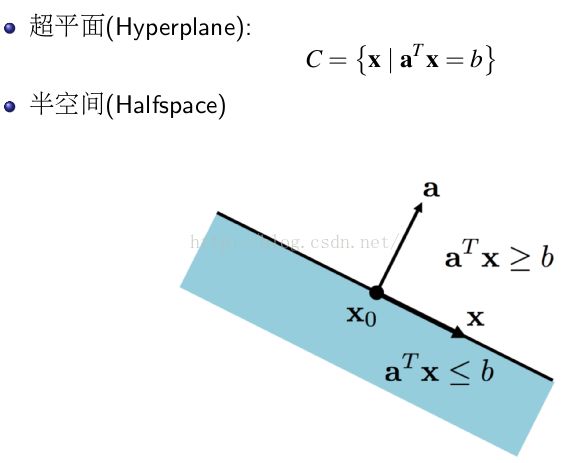
2.3 凸集
举例：
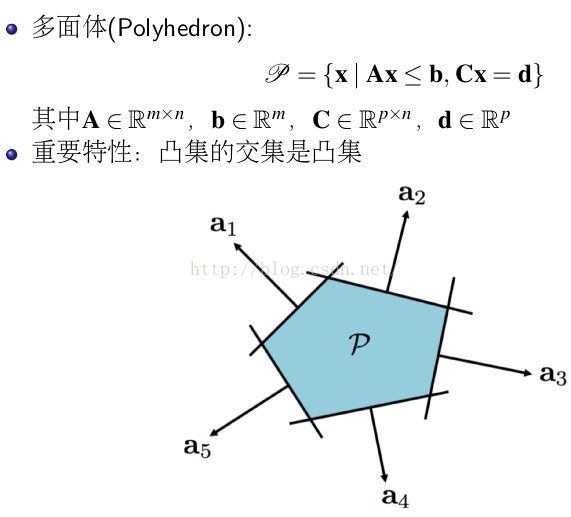
常见的凸集：
2.4 凸函数
几何解释：
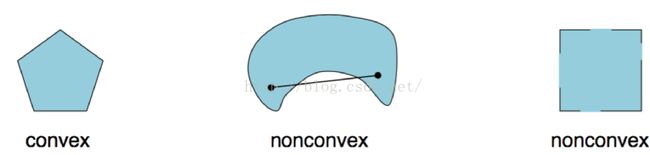
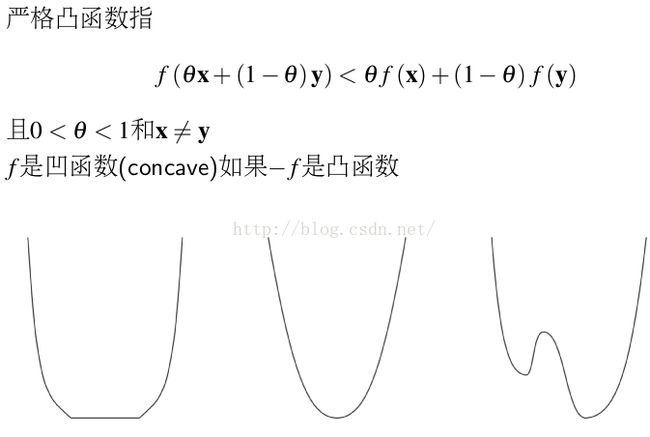
2.5 凸函数和非凸函数直观比较
如第一幅图是凸函数，但是不是严格的图函数。
凸函数的一阶二阶条件
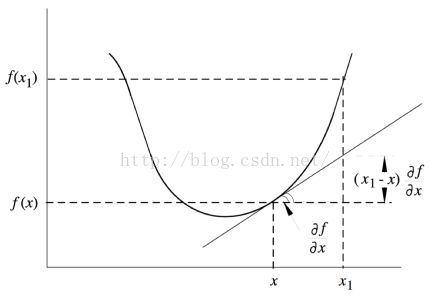
一阶充要条件
几何解释：
二阶充要条件
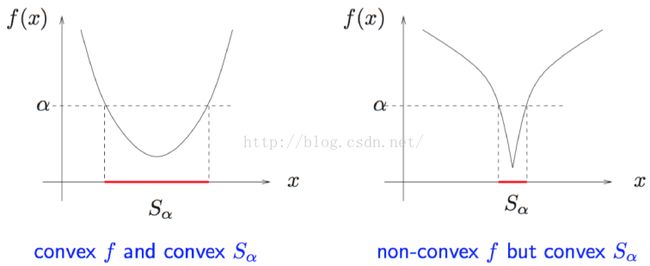
2.6 凸函数和凸集的关系
比如：
第二种情况叫做拟凸函数
2.7 凸优化问题标准形式
对于凸优化问题，简单问题可以用KKT求解，复杂问题可以用梯度下降，拟牛顿问题求解。
但是在实际中，很多问题是非凸的。对于非凸问题，可以通过求其近似的凸优化问题的解作为其初始解，这样会比随机初始化效果好很多。
有些问题在当前维度为非凸，但是在更高的维度上是凸的。
参考资料：
七月算法：机器学习四月班：http://www.julyedu.com/
图片来自于课程PPT