1.硬币游戏:
给出k个数字a1, a2, a3, ..., ak,且至少有一个数字为1(ps:是为了保证最后一定有解,否则当剩下的硬币数比最少的 xi 都要少,就无解了)。一开始有x枚硬币,A、B两人轮流取一定数目硬币,且取的数目必须在集合a1, a2, a3, ..., ak中,取走最后几枚硬币的人获胜,A先取。问:两人都采取最优策略的情况下,谁会获胜?
分析:假设最后轮到某个人取时,没有硬币了,那么这个状态为必败态,可以用dp将状态从0枚硬币开始往前推,
就可以得出所有可能的硬币取值所对应的状态是必胜还是必败。那么,必胜态和必败态之间是怎么转移的呢?
假设在我们面前有s枚硬币,我们可以通过取走x[i]枚,使得剩下的硬币数目为s - x[i] = t。现在我们考虑s和t之间的状态转移:
- 对于s来说,如果任何一种尝试,取走x[i]后得到的t都是必胜态(对方的),那么此时的s就处在一个必败态(自己的)。
- 反过来,如果其中存在某种尝试,使得取走x[i]后得到的t是必败态(对方的),那么我们肯定会沿着这个方向转移,此时的s就一定处在必胜态(自己的)。
由上面的状态转移关系,易得状态转移方程win[i] |= !win[i-a[1...n]](i > a[ j ],且win[i]初始值为false)。就是在i > a[j]的条件下(因为要保证win的索引值为非负),只要存在其中一个win[i-a[j]]为false,就可以使得win[i]必胜。
void solve()
{
win[0] = false; //dp的边界条件,最小的子问题
for(int i = 1; i <= x; ++i)
{
win[i] = false;
for(int j = 0; j < n; ++j)
{
win[i] |= (i > a[j] && !win[i-a[j])
}
}
}
也可以这样写:
void solve()
{
win[0] = false; //dp的边界条件,最小的子问题
for(int j = 0; j < n; ++j)
{
if(i >= a[j])
{
if(win[i - a[j]] == false)
win[i] = true;
}
}
}2.POJ2484 A Funny Game
A Funny Game
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 5341 | Accepted: 3341 |
Description
Alice and Bob decide to play a funny game. At the beginning of the game they pick n(1 <= n <= 10
6) coins in a circle, as Figure 1 shows. A move consists in removing one or two adjacent coins, leaving all other coins untouched. At least one coin must be removed. Players alternate moves with Alice starting. The player that removes the last coin wins. (The last player to move wins. If you can't move, you lose.)
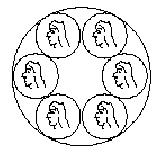
Figure 1
Note: For n > 3, we use c1, c2, ..., cn to denote the coins clockwise and if Alice remove c2, then c1 and c3 are NOT adjacent! (Because there is an empty place between c1 and c3.)
Suppose that both Alice and Bob do their best in the game.
You are to write a program to determine who will finally win the game.
Figure 1
Note: For n > 3, we use c1, c2, ..., cn to denote the coins clockwise and if Alice remove c2, then c1 and c3 are NOT adjacent! (Because there is an empty place between c1 and c3.)
Suppose that both Alice and Bob do their best in the game.
You are to write a program to determine who will finally win the game.
Input
There are several test cases. Each test case has only one line, which contains a positive integer n (1 <= n <= 10
6). There are no blank lines between cases. A line with a single 0 terminates the input.
Output
For each test case, if Alice win the game,output "Alice", otherwise output "Bob".
Sample Input
1 2 3 0
Sample Output
Alice Alice Bob
题意为两人玩一个游戏,桌面上放着n枚硬币,这些硬币围成一个圆,一个人每次可以从中取一枚或者两枚硬币,但是两枚硬币必须连续,问双方都采取最优策略时,谁会获胜。
分析:第一个人第一次取之前,桌面上的硬币围成一个圆,圆上的硬币都是关于圆心对称的,无论第一个人怎么取,都会破坏了对称性,第二个人只要取去根据剩下硬币的数量,取1或者2枚,使得圆环变成了两条完全相同的链,就又构造了一个对方必败的状态,那么到最后,肯定是后手的人获胜。但是注意当n <= 2的时候,先手的人可以直接取完所有硬币。
int n;
void solve()
{
if(n <= 2) cout << "Alice" << endl; //先手胜
else cout << "Bob" << endl; //后手胜
}
3. POJ2348 Euclid's Game
Euclid's Game
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 9036 | Accepted: 3698 |
Description
Two players, Stan and Ollie, play, starting with two natural numbers. Stan, the first player, subtracts any positive multiple of the lesser of the two numbers from the greater of the two numbers, provided that the resulting number must be nonnegative. Then Ollie, the second player, does the same with the two resulting numbers, then Stan, etc., alternately, until one player is able to subtract a multiple of the lesser number from the greater to reach 0, and thereby wins. For example, the players may start with (25,7):
an Stan wins.
25 7
11 7
4 7
4 3
1 3
1 0
an Stan wins.
Input
The input consists of a number of lines. Each line contains two positive integers giving the starting two numbers of the game. Stan always starts.
Output
For each line of input, output one line saying either Stan wins or Ollie wins assuming that both of them play perfectly. The last line of input contains two zeroes and should not be processed.
Sample Input
34 12 15 24 0 0
Sample Output
Stan wins Ollie wins题意:给出两个整数a和b,两人轮流从较大的数字中减去较小数字的k倍,使得相减后的数字非负。在自己的回合将其中一个数变为0的一方获胜,当双方都采取最优策略时,谁会获胜?
分析:不妨设a < b。根据自由度(就是可以选择的操作个数)的观点,我们把a和b的关系分成以下两类。
- a < b < 2*a. 这时候,只有一种可能的操作,就是b-a。
- 2*a < b. 这时候,有至少两种操作,b可以减去a,2*a,3*a,......(至少前两种选择可以保证减完之后b还是正数)。
那么在第一种情况中,我们没有选择的余地,要是b减去a之后为必胜态,那么b就是必败态。反之如果b减去a之后为必败态,b就是必胜态。这里状态只能被对方控制。
在第二种情况中,我们考虑一下假设x是使得 0 < b- ax < a 的整数,当我们让b减去(x-1)a时,就把状态转移到了第一种情况,此时对方并没有选择。如果对方此时处于必败态,那么我们理应这样选择。但是,假如减了(x-1)a之后对方是必胜态,我们应该怎么更换选择呢?很显然,从b中减去xa后的状态是减去(x-1)a后的状态唯一可以转移到的状态,假如减去(x-1)a后的状态为必胜态,减去xa后的状态就为必败态,我们只需将b减去xa即可。
那么也就是说,处于第二种情况的人,有两种选择,其中必然有一种是可以到达(对方的)必败态的,而处于第一种情况的人,是根本没有选择的空间,只能接受对方的支配。
那么我们该怎么判断谁胜出呢?很简单,只要谁能先到达第二种情况,谁就必胜。
void solve()
{
bool turn = false;
while(1)
{
if(a > b) swap(a, b);
if(b % a == 0) break;
if(b < 2*a) b -= a;
else if(2*a < b) break;
turn = !turn ;
}
if(turn == false) cout << "Stan wins" << endl;
else cout << "Ollie wins" << endl;
}