编辑本段发现历史
是由于公元前6世纪 古希腊的 毕达哥拉斯学派研究过 正五边形和正十边形的作图,因此现代 数学家们推断当时 毕达哥拉斯学派已经触及甚至掌握了 黄金分割。
公元前4世纪,古希腊数学家 欧多克索斯第一个 系统研究了这一问题,并建立起 比例理论。他认为所

黄金分割
(4张)
谓黄金分割,指的是把长为L的 线段分为两部分,使其中一部分对于全部之比,等于另一部分对于该部分之比。而计算黄金分割最简单的方法,是计算 斐波那契数列1,1,2,3,5,8,13,21,。..后二数之比2/3,3/5,5/8,8/13,13/21,... 近似值的。
黄金分割在 文艺复兴前后,经过 阿拉伯人传入 欧洲,受到了欧洲人的欢迎,他们称之为"金法",17世纪欧洲的一位 数学家,甚至称它为"各种 算法中最可宝贵的算法"。这种算法在印度称之为"三率法"或"三数法则",也就是我们现在常说的比例方法。
公元前300年前后 欧几里得撰写 《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著。
中世纪后,黄金分割被披上神秘的外衣,意大利数学家帕乔利称中末比为神圣比例,并专门为此著书立说。德国天文学家开普勒称黄金分割为神圣分割。
到19世纪黄金分割这一名称才逐渐通行。黄金分割数有许多有趣的性质,人类对它的实际应用也很广泛:最著名的例子是优选学中的 黄金分割法或0.618法,是由美国数学家 基弗于1953年首先提出的,70年代由华罗庚提倡在 中国推广。
编辑本段几何作法
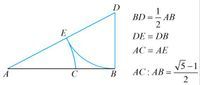
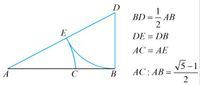
已知线段AB,按照如下方法作图:
(1)经过点B作BD⊥AB,使BD= AB/2。
(2) 连接AD,在DA上截取DE=DB。
(3)在AB上截取AC=AE.则点C为线段AB的黄金分割点。
黄金分割点是指分一线段为两部分,使得原来线段的长跟较长的那部分的比为黄金分割的点。线段上有两个这样的点。 利用线段上的两个黄金分割点,可以作出正五角星,正五边形等。
做黄金分割的一种方法
设一条线段AB的长度为a,C点在靠近B点的黄金分割点上且AC为b AC/AB=BC/AC b^2=a×(a-b) b^2=a^2-ab a^2-ab+(1/4)b^2=(5/4)×b^2 (a-b/2)^2=(5/4)b^2 a-b/2=(√5/2)×b a-b/2=(√5)b/2 a=b/2+(√5)b/2 a/b=(√5+1)/2 ∴b/a=2/(√5+1) b/a=2(√5-1)/(√5+1)(√5-1) b/a=2(√5-1)/4 b/a=(√5-1)/2
编辑本段通常数值
通常用希腊字母φ表示这个值。

黄金分割奇妙在于其比例与其倒数是一样
黄金分割奇妙之处,在于其比例与其倒数是一样的。例如:1.618的 倒数是0.618,而1.618:1与1:0.618是一样的。
确切值为( 根号5-1)/2
黄金分割数是 无理数,前面的2000位为:
0.6180339887 4989484820 4586834365 6381177203 0917980576 : 50
2862135448 6227052604 6281890244 9707207204 1893911374 : 100
8475408807 5386891752 1266338622 2353693179 3180060766 : 150
7263544333 8908659593 9582905638 3226613199 2829026788 : 200
0675208766 8925017116 9620703222 1043216269 5486262963 : 250
1361443814 9758701220 3408058879 5445474924 6185695364 : 300
8644492410 4432077134 4947049565 8467885098 7433944221 : 350
2544877066 4780915884 6074998871 2400765217 0575179788 : 400
3416625624 9407589069 7040002812 1042762177 1117778053 : 450
1531714101 1704666599 1466979873 1761356006 7087480710 : 500
1317952368 9427521948 4353056783 0022878569 9782977834 : 550
7845878228 9110976250 0302696156 1700250464 3382437764 : 600
8610283831 2683303724 2926752631 1653392473 1671112115 : 650
8818638513 3162038400 5222165791 2866752946 5490681131 : 700
7159934323 5973494985 0904094762 1322298101 7261070596 : 750
1164562990 9816290555 2085247903 5240602017 2799747175 : 800
3427775927 7862561943 2082750513 1218156285 5122248093 : 850
9471234145 1702237358 0577278616 0086883829 5230459264 : 900
7878017889 9219902707 7690389532 1968198615 1437803149 : 950
9741106926 0886742962 2675756052 3172777520 3536139362 : 1000
1076738937 6455606060 5921658946 6759551900 4005559089 : 1050
5022953094 2312482355 2122124154 4400647034 0565734797 : 1100
6639723949 4994658457 8873039623 0903750339 9385621024 : 1150
2369025138 6804145779 9569812244 5747178034 1731264532 : 1200
2041639723 2134044449 4873023154 1767689375 2103068737 : 1250
8803441700 9395440962 7955898678 7232095124 2689355730 : 1300
9704509595 6844017555 1988192180 2064052905 5189349475 : 1350
9260073485 2282101088 1946445442 2231889131 9294689622 : 1400
0023014437 7026992300 7803085261 1807545192 8877050210 : 1450
9684249362 7135925187 6077788466 5836150238 9134933331 : 1500
2231053392 3213624319 2637289106 7050339928 2265263556 : 1550
2090297986 4247275977 2565508615 4875435748 2647181414 : 1600
5127000602 3890162077 7322449943 5308899909 5016803281 : 1650
1219432048 1964387675 8633147985 7191139781 5397807476 : 1700
1507722117 5082694586 3932045652 0989698555 6781410696 : 1750
8372884058 7461033781 0544439094 3683583581 3811311689 : 1800
9385557697 5484149144 5341509129 5407005019 4775486163 : 1850
0754226417 2939468036 7319805861 8339183285 9913039607 : 1900
2014455950 4497792120 7612478564 5916160837 0594987860 : 1950
0697018940 9886400764 4361709334 1727091914 3365013715 : 2000
编辑本段美学价值
因为它在造型 艺术中具有 美学价值,在工艺美术和日用品的长宽设计中,采用这一比值能够引起人们的美感,在实际生活中的应用也非常广泛,建筑物中某些线段的比就科学采用了黄金分割,舞台上的报幕员并不是站在舞台的正中央,而是偏在台上一侧,以站在舞台长度的黄金分割点的位置最美观,声音传播的最好。就连植物界也有采用黄金分割的地方,如果从一棵嫩枝的顶端向下看,就会看到叶子是按照黄金分割的规律排列着的。在很多科学实验中,选取方案常用一种0.618法,即 优选法,它可以使我们合理地安排较少的试验次数找到合理的西方和合适的工艺条件。正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用,所以人们才珍贵地称它为"黄金分割"。
黄金分割(Golden Section)是一种数学上的比例关系。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。应用时一般取0.618 ,就像 圆周率在应用时取3.14一样。
。并且人们认为如果符合这一比例的话,就会显得更美、更好看、更协调。在生活中,对“黄金分割”有着很多的应用。
最完美的人体:肚脐到脚底的距离/头顶到脚底的距离=0.618
最漂亮的脸庞:眉毛到脖子的距离/头顶到脖子的距离=0.618
在 企业经营管理中,从经验来看,资产负债率(即负债总额除资产总额)应以黄金分割点为 临界点,如果高于这个点就可能面临较大经营风险(当然象银行这类企业可以例外),目前正在进行科学论证中。
举例与应用
这个数值的作用不仅仅体现在诸如 绘画、 雕塑、 音乐、 建筑等艺术领域,而且在 管理、 工程设计等方面也有着不可忽视的作用。
让我们首先从一个数列开始,它的前面几个数是:1、1、2、3、5、8、13、21、34、55、89、144…。.这个数列的名字叫做" 菲波那契数列",这些数被称为"菲波那契数"。特点是即除前两个数(数值为1)之外,每个数都是它前面两个数之和。
菲波那契数列与黄金分割有什么关系呢?经研究发现,相邻两个菲波那契数的比值是随序号的增加而逐渐趋于 黄金分割比的。即f(n)/f(n-1)-→1.618…。由于菲波那契数都是 整数,两个整数相除之商是 有理数,所以只是逐渐逼近黄金分割比这个无理数。但是当我们继续计算出后面更大的菲波那契数时,就会发现相邻两数之比确实是非常接近黄金分割比的。
一个很能说明问题的例子是 五角星/正五边形。五角星是非常美丽的,我们的国旗上就有五颗,还有不少国家的 国旗也用五角星,这是为什么?因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的。正五边形 对角线连满后出现的所有三角形,都是黄金分割三角形。
由于五角星的顶角是36度,这样也可以得出黄金分割的数值为2Sin18度。
编辑本段生活实例
植物叶子
,千姿百态,生机盎然,给大自然带来了美丽的 绿色世界。尽管叶子形状随种而异,但它在茎上的排列顺序(称为叶序),却是极有规律的。
你从植物茎的顶端向下看,经细心观察,发现上下层中相邻的两片叶子之间约成137.5°角。如果每层叶子只画一片来代表,第一层和第二层的相邻两叶之间的角度差约是137.5°,以后二到三层,三到四层,四到五层……两叶之间都成这个角度数。植物学家经过计算表明:这个角度对叶子的采光、通风都是最佳的。叶子的排布,多么精巧!
今人惊讶的是,人体自身也和0.618密切相关。对人体解剖很有研究的意大利画家 达·芬奇发现,人的肚脐位于身长的0.618处。科学家们还发现,当外界环境温度为人体温度的0.618倍时,人会感到最舒服。
古希腊帕提依神庙由于高和宽的比是0.618,成了举世闻名的完美建筑。建筑师们发现,按这样的比例来设计殿堂,殿堂更加雄伟、壮丽;去设计别墅,别墅将更加舒适、美丽。连一扇门窗若设计为黄金矩形都会显得更加协调和令人赏心悦目。
高雅的艺术殿堂里,自然也留下了 黄金数的足迹。画家们发现,按0.618∶1来设计腿长与身高的比例,画出的人体身材最优美,而现今的女性,腰身以下的长度平均只占身高的0.58,因此古 希腊维纳斯女塑像及 太阳神阿波罗的形象都通过故意延长双腿,使之与身高的比值为0.618,从而创造艺术美。难怪许多姑娘都愿意穿上高跟鞋,而 芭蕾舞演员则在翩翩起舞时,不时地踮起脚尖。
音乐家发现,二胡演奏中,“千金”分弦的比符合0.618∶1时,奏出来的音调最和谐、最悦耳。
只要留心,到处都可发现黄金数这位美的“使者”的足迹。运用于科学实验和工农业生产的优选法中的0.618法,还能给我们带来巨大的经济效益呢!黄金数0.618,真是一件造福人类的绚丽瑰宝!
希腊古城雅典有一座用大理石砌成的神庙,神庙大殿中央的女神像是用象牙和黄金雕成的。女神的体态轻柔优美,引人入胜。经专家研究发现,她的身体从脚跟到肚脐间的距离与整个身高的比值,恰好是0.618。不仅雅典娜女神身材如此美好,其他许多希腊女神的身体比例也是如此。人们所熟悉的米洛斯“维纳斯”,太阳神阿波罗的形象,海姑娘―― 阿曼等一些名垂千古的雕像,都可以找到0.618的比值。
1483年左右, 达芬奇画的一副未完成的油画,包围着 圣杰罗姆躯体的黑线,就是一个黄金分割的矩形,当时达芬奇似乎有意利用这一黄金分割的比值。“检阅”是法国印象派画家舍勒特的一副油画,它的画杠结构比例也正是0.618的比值。 英国在画家斐拉克曼的名著《 希腊的神话和传说》一书中,工绘有96幅美人图。每一幅画上的美人都妩媚无比婀娜多姿。如果仔细量一下她们的比例也都和雅典娜相似。
建筑:早在公元前五世纪, 希腊建筑家就知道0.618的比值是协调,平衡的结构。 文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边长与高之比都接近于0.618。古时候的一些神庙,在建筑时高和宽也是按黄金数的比来建立,他们认为这样的长方形看来是较美观。黄金律是建筑艺术必须遵循的规律。在建筑造型上,人们在高塔的黄金分割点处建楼阁或设计平台,便能使平直单调的塔身变得丰富多彩。
据研究,从猿到人的进化过程中,骨骼方面以头骨和腿骨变化最大,躯体外形由于近似黄金而矩形变化最小,人体结构中有许多比例关系接近0.618,从而使人体美在几十万年的历史积淀中固定下来。人类最熟悉自己,势必将人体美作为最高的审美标准,由物及人,由人及物,推而广之,凡是与人体相似的物体就喜欢它,就觉得美。于是黄金分割律作为一种重要形式美法则,成为世代相传的审美经典规律,至今不衰!近年来,在研究黄金分割与人体关系时,发现了人体结构中有14个“黄金点”,12个“黄金矩形”和2个“黄金 指数” 黄金点:(1)肚脐:头顶-足底之分割点;(2)咽喉:头顶-肚脐之分割点;(3)、(4)膝关节:肚脐-足底之分割点;(5)、(6)肘关节:肩关节-中指尖之分割点;(7)、(8)乳头:躯干乳头纵轴上这分割点;(9)眉间点:发际-颏底间距上1/3与中下2/3之分割点;(10)鼻下点:发际-颏底间距下1/3与上中2/3之分割点;(11)唇珠点:鼻底-颏底间距上1/3与中下2/3之分割点;(12)颏唇沟正路点:鼻底-颏底间距下1/3与上中2/3之分割点;(13)左口角点:口裂水平线左1/3与右2/3之分割点;(14) 右口角点:口裂水平线右1/3与左2/3之分割点。 面部黄金分割律 面部三庭五眼 黄金矩形:(1)躯体轮廓:肩宽与臀宽的 平均数为宽,肩峰至臀底的高度为长;(2)面部轮廓:眼水平线的面宽为宽,发际至颏底间距为长;(3)鼻部轮廓:鼻翼为宽,鼻根至鼻底间距为长;(4)唇部轮廓:静止状态时上下唇峰间距为宽,口角间距为长;(5)、(6)手部轮廓:手的横径为宽,五指并拢时取平均数为长;(7)、(8)、(9)、(10)、(11)、(12)上颌切牙、侧切牙、尖牙(左右各三个)轮廓:最大的近远中径为宽,齿龈径为长。
(二)比例关系 是用 数字来表示人体美,并根据一定的基准进行比较。用同一人体的某一部位作为基准,来判定它与人体的比例关系的方法被称为同身方法(见中图)。分为三组: 系数法,常指头高身长指数,如画人体有坐五、立七,即身高在坐位时为头高的五倍、立位时为7或7.5倍;百 分数法,将身长视为100%,身体各部位在其中的比例;两分法:即把人体分成大小两部分,大的部分从脚到脐,小的部分为脐到头顶。标准的面型,其长宽比例协调,符合三停五眼(见右图)。三停是指脸型的长度,从头部发际到下颏的距离分为三等分,即从发际到眉、眉到鼻尖、鼻尖到下颏各分为一等分,各称一停共三停;五眼是指脸型的宽度,双耳间正面 投影的长度为五只眼裂的长度,除眼裂外、内此间距为一眼裂长度、两侧外眦角到耳部各 有一眼裂长度,其是五眼长度称五眼。
(三)角度关系 从不同的角度观察,所反映的人体形态也各不相同。Belt和Campen等人提出的侧角学说,就是通过角度来体现人体形体美的。其中Campen的学说是以鼻下点与耳孔点的 直线连线为基准,来测量侧面观察时额头的倾斜角度的方法,这样可以把复杂的立体感的头部,用简单的轮廓线进行描述-被称为侧面定性分析方法。用连接鼻尖点和颏下点的直线来观察唇的突出度,评价面下部的美丑。鼻尖、下唇红前缘、颏下点在同一条直线上,称为Ricketts美学 平面,是一种美的标志。