机器学习分类算法(六)-随机森林算法

集成算法

集成学习（ensemble learning）是目前非常流行的机器学习策略，基本上所有问题都可以借用其思想来得到效果上的提升。基本出发点就是把算法和各种策略集中在一起，说白了就是一个搞不定大家一起上！集成学习既可以用于分类问题，也可以用于回归问题，在机器学习领域会经常看到它的身影，本章就来探讨一下几种经典的集成策略，并结合其应用进行通俗解读。

Bagging算法

集成算法有3个核心的思想：bagging、boosting和stacking，这几种集成策略还是非常好理解的，下面向大家逐一介绍。

并行的集成

Bagging即boostrap aggregating，其中boostrap是一种有放回的抽样方法，抽样策略是简单的随机抽样。其原理很直接，把多个基础模型放到一起，最后再求平均值即可，这里可以把决策树当作基础模型，其实基本上所有集成策略都是以树模型为基础的，公式如下：
$$f(x)=\frac{1}{M}\sum _{m=1}^M{f}_m(x)$$
首先对数据集进行随机采样，分别训练多个树模型，最终将其结果整合在一起即可，思想还是非常容易理解的，其中最具代表性的算法就是随机森林。

随机森林

随机森林是机器学习中十分常用的算法，也是bagging集成策略中最实用的算法之一。那么随机和森林分别是什么意思呢？森林应该比较好理解，分别建立了多个决策树，把它们放到一起不就是森林吗？这些决策树都是为了解决同一任务建立的，最终的目标也都是一致的，最后将其结果来平均即可，如图8-1所示。

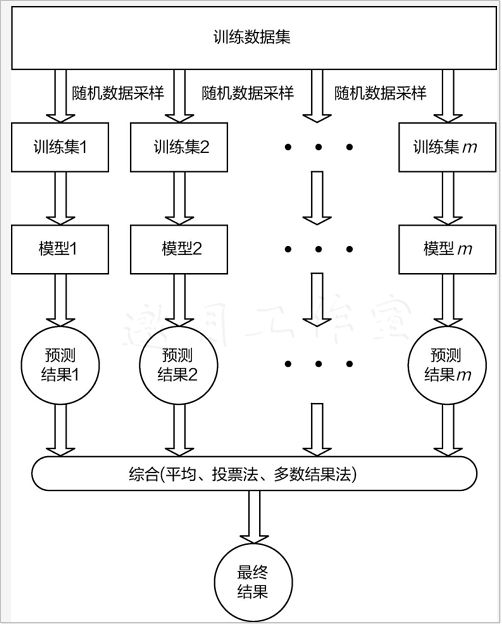
想要得到多个决策树模型并不难，只需要多次建模就可以。但是，需要考虑一个问题，如果每一个树模型都相同，那么最终平均的结果也相同。为了使得最终的结果能够更好，通常希望每一个树模型都是有个性的，整个森林才能呈现出多样性，这样再求它们的平均，结果应当更稳定有效。

如何才能保证多样性呢？如果输入的数据是固定的，模型的参数也是固定的，那么，得到的结果就是唯一的，如何解决这个问题呢？此时就需要随机森林中的另一部分—随机。这个随机一般叫作二重随机性，因为要随机两种方案，下面分别进行介绍。

首先是数据采样的随机，训练数据取自整个数据集中的一部分，如果每一个树模型的输入数据都是不同的，例如随机抽取80%的数据样本当作第一棵树的输入数据，再随机抽取80%的样本数据当作第二棵树的输入数据，并且还是有放回的采样，这就保证两棵树的输入是不同的，既然输入数据不同，得到的结果必然也会有所差异，这是第一重随机。

如果只在数据层面上做文章，那么多样性肯定不够，还需考虑一下特征，如果对不同的树模型选择不同的特征，结果的差异就会更大。例如，对第一棵树随机选择所有特征中的60%来建模，第二棵再随机选择其中60%的特征来建模，这样就把差异放大了，这就是第二重随机。

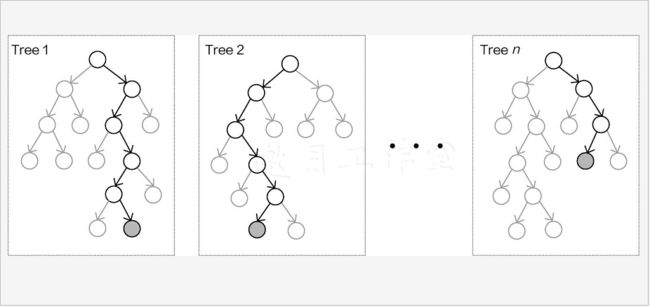
如上图所示，由于二重随机性使得创建出来的多个树模型各不相同，即便是同样的任务目标，在各自的结果上也会出现一定的差异，随机森林的目的就是要通过大量的基础树模型找到最稳定可靠的结果，如下图所示，最终的预测结果由全部树模型共同决定。

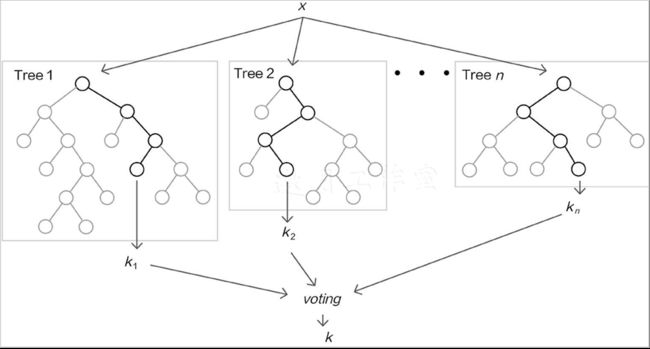
解释随机森林的概念之后，再把它们组合起来总结如下：

• 1.随机森林首先是一种并联的思想，同时创建多个树模型，它们之间是不会有任何影响的，使用相同参数，只是输入不同。
• 2.为了满足多样性的要求，需要对数据集进行随机采样，其中包括样本随机采样与特征随机采样，目的是让每一棵树都有个性。
• 3.将所有的树模型组合在一起。在分类任务中，求众数就是最终的分类结果；在回归任务中，直接求平均值即可。

对随机森林来说，还需讨论一些细节问题，例如树的个数是越多越好吗？树越多代表整体的能力越强，但是，如果建立太多的树模型，会导致整体效率有所下降，还需考虑时间成本。在实际问题中，树模型的个数一般取100～200个，继续增加下去，效果也不会发生明显改变。

下图是随机森林中树模型个数对结果的影响，可以发现，随着树模型个数的增加，在初始阶段，准确率上升很明显，但是随着树模型个数的继续增加，准确率逐渐趋于稳定，并开始上下浮动。这都是正常现象，因为在构建决策树的时候，它们都是相互独立的，很难保证把每一棵树都加起来之后会比原来的整体更好。当树模型个数达到一定数值后，整体效果趋于稳定，所以树模型个数也不用特别多，够用即可。

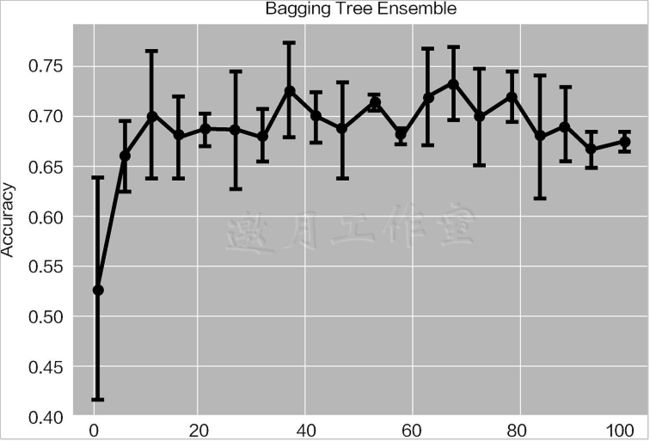
在集成算法中，还有一个很实用的参数——特征重要性，如下图所示。先不用管每一个特征是什么，特征重要性就是在数据中每一个特征的重要程度，也就是在树模型中，哪些特征被利用得更多，因为树模型会优先选择最优价值的特征。在集成算法中，会综合考虑所有树模型，如果一个特征在大部分基础树模型中都被使用并且靠近根节点，它自然比较重要。

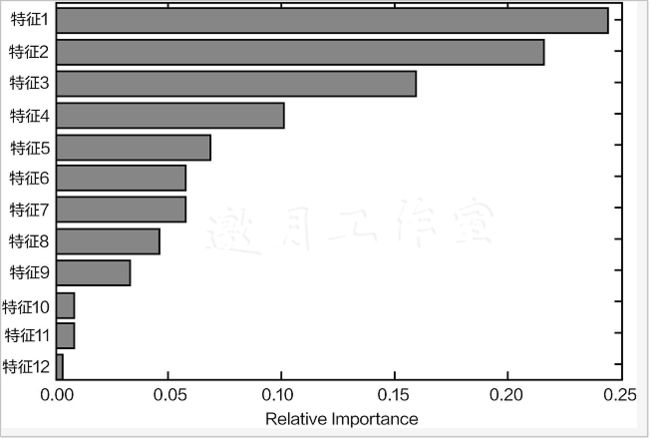
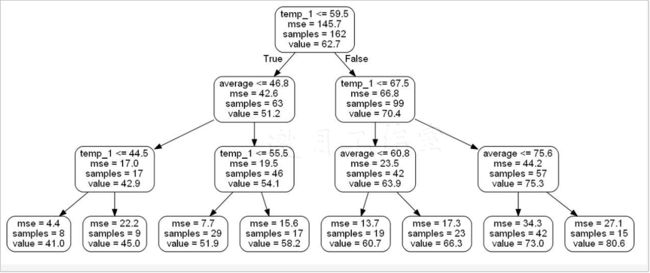
当使用树模型时，可以非常清晰地得到整个分裂过程，方便进行可视化分析，如图8-6所示，这也是其他算法望尘莫及的，在后面的实战任务中将展示绘制树模型的可视化结果的过程。

最后再来总结一下bagging集成策略的特点：

• 1.并联形式，可以快速地得到各个基础模型，它们之间不会相互干扰，但是其中也存在问题，不能确保加进来的每一个基础树模型都对结果产生促进作用，可能有个别树模型反而拉后腿。

• 2.可以进行可视化展示，树模型本身就具有这个优势，每一个树模型都具有实际意义。

• 3.相当于半自动进行特征选择，总是会先用最好的特征，这在特征工程中一定程度上省时省力，适用于较高维度的数据，并且还可以进行特征重要性评估。

Boosting算法

上一节介绍的bagging思想是，先并行训练一堆基础树模型，然后求平均。这就出现了一个问题：如果每一个树模型都比较弱，整体平均完还是很弱，那么怎样才能使模型的整体战斗力更强呢？这回轮到boosting算法登场了，boosting算法可以说是目前比较厉害的一种策略。

串行的集成

Boosting算法的核心思想就在于要使得整体的效果越来越好，整体队伍是非常优秀的，一般效果的树模型想加入进来是不行的，只要最强的树模型。怎么才能做到呢？先来看一下boosting算法的基本公式：
$$F_n(x)=F_{m-1}(x)+{\mathrm{argmin}}_h\sum _{i=1}^{n}L\left(y_i,F_{m-1}\left(x_i\right)+h\left(x_i\right)\right)$$

通俗的解释就是把$F_{m-1}(x)$当作前一轮得到的整体，这个整体中可能已经包含多个树模型，当再往这个整体中加入一个树模型的时候，需要满足一个条件——新加入的$h(x_i)$与前一轮的整体组合完之后，效果要比之前好。怎么评估这个好坏呢？就是看整体模型的损失是不是有所下降。

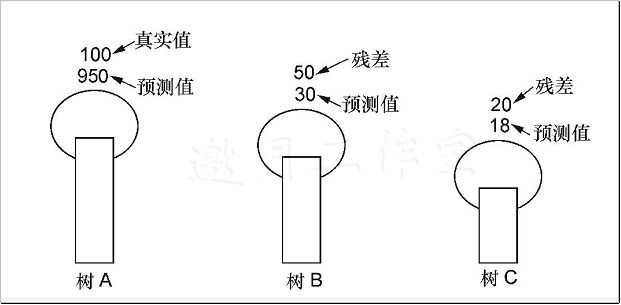
Boosting算法是一种串联方式，如下图所示，先有第一个树模型，然后不断往里加入一个个新的树模型，但是有一个前提，就是新加入的树模型要使得其与之前的整体组合完之后效果更好，说明要求更严格。最终的结果与bagging也有明显的区别，这里不需要再取平均值，而是直接把所有树模型的结果加在一起。那么，为什么这么做呢？

回到银行贷款的任务中，假设数据的真实值等于1000，首先对树A进行预测，得到值950，看起来还不错。接下来树B登场了，这时出现一个关键点，就是它在预测的时候，并不是要继续预测银行可能贷款多少，而是想办法弥补树A还有多少没做好，也就是1000−950=50，可以把50当作残差，这就是树B要预测的结果，假设得到30。现在需要把树A和树B组合成为一个整体，它们一起预测得950+30=980。接下来树C要完成的就是剩下的残差（也就是20），那么最终的结果就是树A、B、C各自的结果加在一起得950+30+18=998，如下图所示。说到这里，相信大家已经有点感觉了，boosting算法好像开挂了，为了达到目标不择手段！没错，这就是boosting算法的基本出发点。

Adaboost算法

下面再来介绍一下boosting算法中的一个典型代表——Adaboost算法。简单来说，Adaboost算法还是按照boosting算法的思想，要建立多个基础模型，一个个地串联在一起。

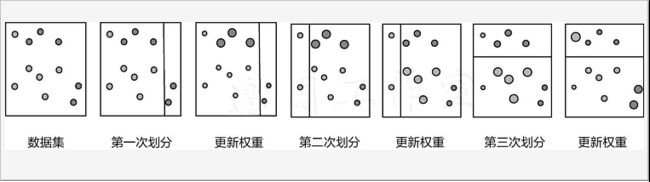
下图是Adaboost算法的建模流程。当得到第一个基础树模型之后，在数据集上有些样本分正确，有些样本分错误。此时需要考虑这样一个问题，为什么会分错呢？是不是因为这些样本比较难以判断吗？那么更应当注重这些难度较大的，也就是需要给样本不同的权重，做对的样本，权重相对较低，因为已经做得很好，不需要太多额外的关注；做错的样本权重就要增大，让模型能更重视它。以此类推，每一次划分数据集时，都会出现不同的错误样本，继续重新调整权重，以对数据集不断进行划分即可。每一次划分都相当于得到一个基础的树模型，它们要的目标就是优先解决之前还没有划分正确的样本。

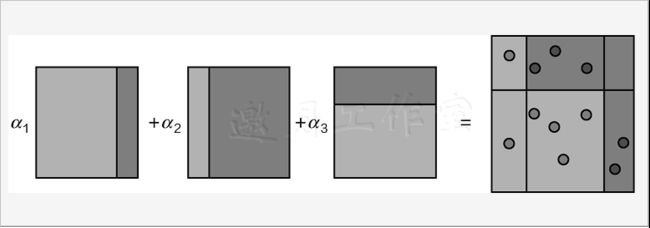
下图是Adaboost算法需要把之前的基础模型都串在一起得到最终结果，但是这里引入了系数，相当于每一个基础模型的重要程度，因为不同的基础模型都会得到其各自的评估结果，例如准确率，在把它们串在一起的时候，也不能同等对待，效果好的让它多发挥作用，效果一般的，让它参与一下即可，这就是系数的作用。

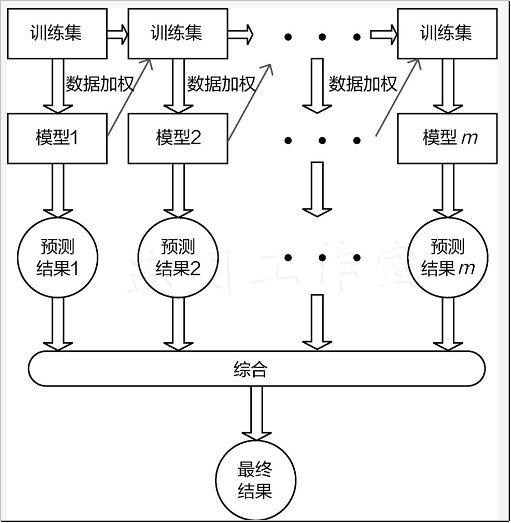
Adaboost算法整体计算流程如下图所示，在训练每一个基础树模型时，需要调整数据集中每个样本的权重分布，由于每次的训练数据都会发生改变，这就使得每次训练的结果也会有所不同，最终再把所有的结果累加在一起。

Stacking模型

前面讨论了bagging和boosting算法，它们都是用相同的基础模型进行不同方式的组合，而stacking模型与它们不同，它可以使用多个不同算法模型一起完成一个任务，先来看看它的整体流程，如下图所示。

首先选择m个不同分类器分别对数据进行建模，这些分类器可以是各种机器学习算法，例如树模型、逻辑回归、支持向量机、神经网络等，各种算法分别得到各自的结果，这可以当作第一阶段。再把各算法的结果（例如得到了4种算法的分类结果，二分类中就是0/1值）当作数据特征传入第二阶段的总分类器中，此处只需选择一个分类器即可，得到最终结果。

其实就是把无论多少维的特征数据传入各种算法模型中，例如有4个算法模型，得到的结果组合在一起就可以当作一个4维结果，再将其传入到第二阶段中得到最终的结果。

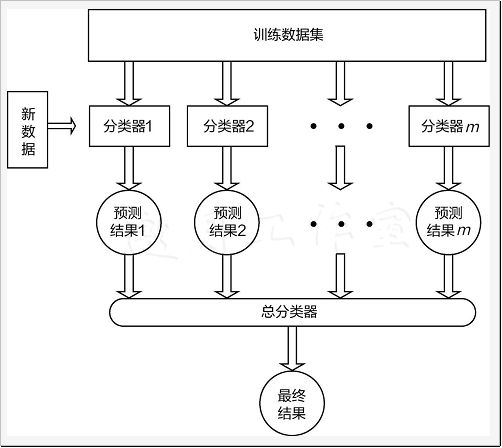
下图是stacking策略的计算细节，其中Model1可以当作是第一阶段中的一个算法，它与交叉验证原理相似，先将数据分成多份，然后各自得到一个预测结果。那么为什么这么做呢？直接拿原始数据进行训练不可以吗？其实在机器学习中，一直都遵循一个原则，就是不希望训练集对接下来任何测试过程产生影响。在第二阶段中，需要把上一步得到的结果当作特征再进行建模，以得到最终结果，如果在第一阶段中直接使用全部训练集结果，相当于第二阶段中再训练的时候，已经有一个先验知识，最终结果可能出现过拟合的风险。

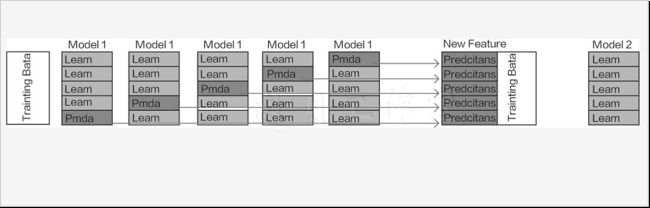
借助于交叉验证的思想，在第一阶段中，恰好可以避免重复使用训练集的问题，这个时候得到的结果特征就是不带有训练集信息的结果。第二阶段就用Model2指代，只需简单完成一次建模任务即可。

随机森林项目实战–气温预测

前面已经讲解过随机森林的基本原理，本节将从实战的角度出发，借助Python工具包完成气温预测任务，其中涉及多个模块，主要包含随机森林建模、特征选择、效率对比、参数调优等。

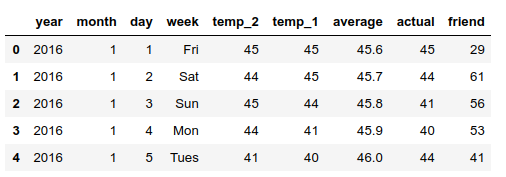
随机森林建模：气温预测的任务目标就是使用一份天气相关数据来预测某一天的最高温度，属于回归任务，首先观察一下数据集：

import pandas as pd
features=pd.read_csv('/home/anti/anaconda3/code/KNN/temps.csv')
features.head(5)

输出结果中表头的含义如下。

• year,moth,day,week：分别表示的具体的时间。
• temp_2：前天的最高温度值。
• temp_1：昨天的最高温度值。
• average：在历史中，每年这一天的平均最高温度值。
• actual：就是标签值，当天的真实最高温度。
• friend：这一列可能是凑热闹的，你的朋友猜测的可能值，不管它就好。

该项目实战主要完成以下3项任务。

1.使用随机森林算法完成基本建模任务：包括数据预处理、特征展示、完成建模并进行可视化展示分析。

2.分析数据样本量与特征个数对结果的影响：在保证算法一致的前提下，增加数据样本个数，观察结果变化。重新考虑特征工程，引入新特征后，观察结果走势。

3.对随机森林算法进行调参，找到最合适的参数：掌握机器学习中两种经典调参方法，对当前模型选择最合适的参数。

特征可视化与预处理

拿到数据之后，一般都会看看数据的规模，做到心中有数：

输出结果显示该数据一共有348条记录，每个样本有9个特征。如果想进一步观察各个指标的统计特性，可以用.describe()展示：

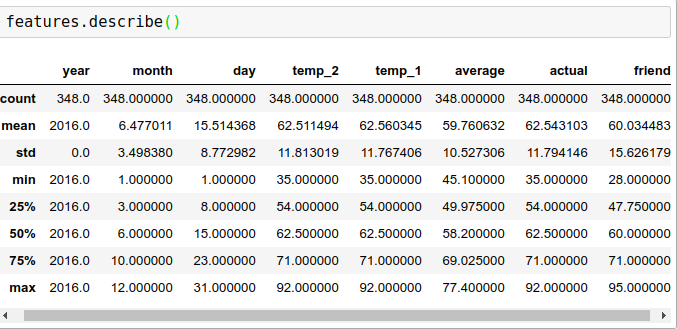
输出结果展示了各个列的数量，如果有数据缺失，数量就会有所减少。由于各列的统计数量值都是348，所以表明数据集中并不存在缺失值，并且均值、标准差、最大值、最小值等指标都在这里显示。

对于时间数据，也可以进行格式转换，原因在于有些工具包在绘图或者计算的过程中，用标准时间格式更方便：

# 处理时间数据
import datetime

# 分别得到年，月，日
years = features['year']
months = features['month']
days = features['day']

# datetime格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]
dates[:5]

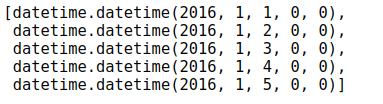
为了更直观地观察数据，最简单有效的办法就是画图展示，首先导入Matplotlib工具包，再选择一个合适的风格（其实风格差异并不是很大）：

# 准备画图
import matplotlib.pyplot as plt

# 指定默认风格
plt.style.use('fivethirtyeight')

开始布局，需要展示4项指标，分别为最高气温的标签值、前天、昨天、朋友预测的气温最高值。既然是4个图，不妨采用2×2的规模，这样会更清晰，对每个图指定好其图题和坐标轴即可：

# 设置布局
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize = (10,10))
fig.autofmt_xdate(rotation = 45)

# 标签值
ax1.plot(dates, features['actual'])
ax1.set_xlabel(''); ax1.set_ylabel('Temperature'); ax1.set_title('Max Temp')

# 昨天
ax2.plot(dates, features['temp_1'])
ax2.set_xlabel(''); ax2.set_ylabel('Temperature'); ax2.set_title('Previous Max Temp')

# 前天
ax3.plot(dates, features['temp_2'])
ax3.set_xlabel('Date'); ax3.set_ylabel('Temperature'); ax3.set_title('Two Days Prior Max Temp')

# 我的逗逼朋友
ax4.plot(dates, features['friend'])
ax4.set_xlabel('Date'); ax4.set_ylabel('Temperature'); ax4.set_title('Friend Estimate')

plt.tight_layout(pad=2)

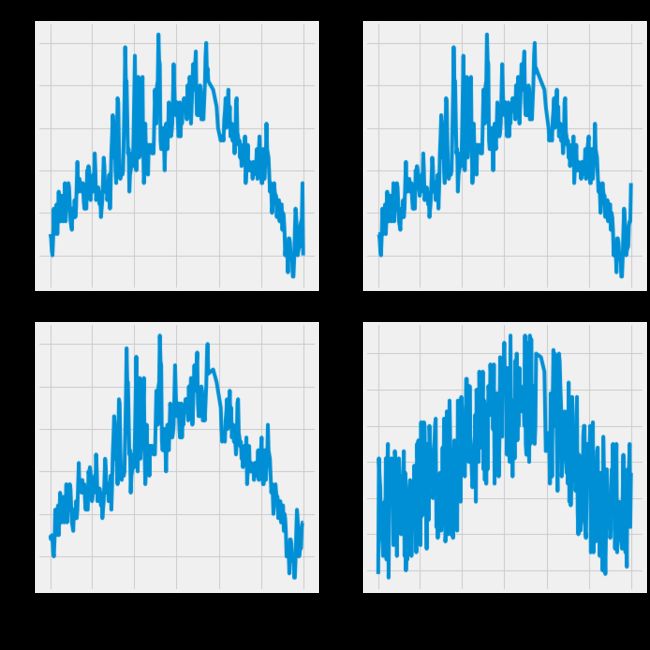
由图可见，各项指标看起来还算正常（由于是国外的天气数据，在统计标准上有些区别）。接下来，考虑数据预处理的问题，原始数据中的week列并不是一些数值特征，而是表示星期几的字符串，计算机并不认识这些数据，需要转换一下。

下图是常用的转换方式，称作one-hot encoding或者独热编码，目的就是将属性值转换成数值。对应的特征中有几个可选属性值，就构造几列新的特征，并将其中符合的位置标记为1，其他位置标记为0。

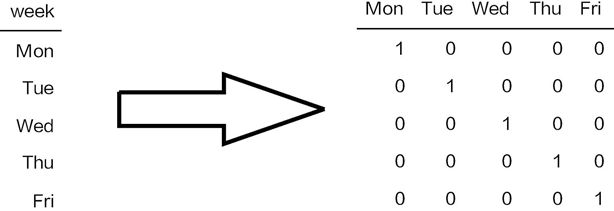
既可以用Sklearn工具包中现成的方法完成转换，也可以用Pandas中的函数，综合对比后觉得用Pandas中的get_dummies()函数最容易：

features=pd.get_dummies(features)
features.head(5)

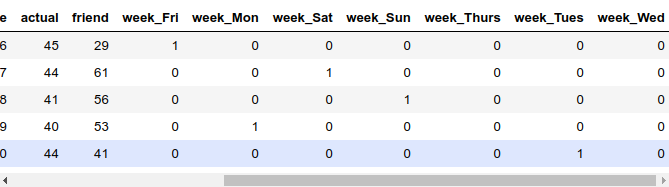
完成数据集中属性值的预处理工作后，默认会把所有属性值都转换成独热编码的格式，并且自动添加后缀，这样看起来更清晰。

其实也可以按照自己的方式设置编码特征的名字，在使用时，如果遇到一个不太熟悉的函数，想看一下其中的细节，一个更直接的方法，就是在Notebook中直接调用help工具来看一下它的API文档，下面返回的就是get_dummies的细节介绍，也可以查阅在线文档
　　
特征预处理完成之后，还要把数据重新组合一下，特征是特征，标签是标签，分别在原始数据集中提取一下：

# 数据与标签
import numpy as np

# 标签
labels = np.array(features['actual'])

# 在特征中去掉标签
features= features.drop('actual', axis = 1)

# 名字单独保存一下，以备后患
feature_list = list(features.columns)

# 转换成合适的格式
features = np.array(features)

在训练模型之前，需要先对数据集进行切分：

# 数据集切分
from sklearn.model_selection import train_test_split

train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size = 0.25,
                                                                           random_state = 42)
print('训练集特征:', train_features.shape)
print('训练集标签:', train_labels.shape)
print('测试集特征:', test_features.shape)
print('测试集标签:', test_labels.shape)

随机森林回归模型

万事俱备，开始建立随机森林模型，首先导入工具包，先建立1000棵树模型试试，其他参数暂用默认值，然后深入调参任务：

# 导入算法
from sklearn.ensemble import RandomForestRegressor

# 建模
rf = RandomForestRegressor(n_estimators= 1000, random_state=42)

# 训练
rf.fit(train_features, train_labels)

RandomForestRegressor(bootstrap=True, ccp_alpha=0.0, criterion='mse',
                      max_depth=None, max_features='auto', max_leaf_nodes=None,
                      max_samples=None, min_impurity_decrease=0.0,
                      min_impurity_split=None, min_samples_leaf=1,
                      min_samples_split=2, min_weight_fraction_leaf=0.0,
                      n_estimators=1000, n_jobs=None, oob_score=False,
                      random_state=42, verbose=0, warm_start=False)

由于数据样本量非常小，所以很快可以得到结果，这里选择先用MAPE指标进行评估，也就是平均绝对百分误差。

# 预测结果
predictions = rf.predict(test_features)

# 计算误差
errors = abs(predictions - test_labels)

# mean absolute percentage error (MAPE)
mape = 100 * (errors / test_labels)

print ('MAPE:',np.mean(mape))

最终结果是：MAPE: 6.011244187972058

其实对于回归任务，评估方法还是比较多的，下面列出几种，都很容易实现，也可以选择其他指标进行评估。

树模型可视化方法

得到随机森林模型后，现在介绍怎么利用工具包对树模型进行可视化展示，首先需要安装Graphviz工具，其配置过程如下。

第① 步：下载安装。

登录网站

下载graphviz-2.38.msi，完成后双击这个msi文件，然后一直单击next按钮，即可安装Graphviz软件（注意：一定要记住安装路径，因为后面配置环境变量会用到路径信息，系统默认的安装路径是C:\Program Files (x86)\Graphviz2.38）。

ubuntu版本只需要一条命令即可：

sudo apt-get install graphviz

第②步：配置环境变量。

将Graphviz安装目录下的bin文件夹添加到Path环境变量中。

第③步：验证安装。

进入Windows命令行界面，输入“dot–version”命令，然后按住Enter键，如果显示Graphviz的相关版本信息，则说明安装配置成功，

最后还需安装graphviz、pydot和pydotplus插件，在命令行中输入相关命令即可，代码如下：

pip install graphviz
pip install pydot2
pip install pydotplus
pip install pydot

上述工具包安装完成之后，就可以绘制决策树模型：

# 导入所需工具包
from sklearn.tree import export_graphviz
import pydot 

# 拿到其中的一棵树
tree = rf.estimators_[5]

# 导出成dot文件
export_graphviz(tree, out_file = 'tree.dot', feature_names = feature_list, rounded = True, precision = 1)

# 绘图
(graph, ) = pydot.graph_from_dot_file('tree.dot')

# 展示
graph.write_png('tree.png');

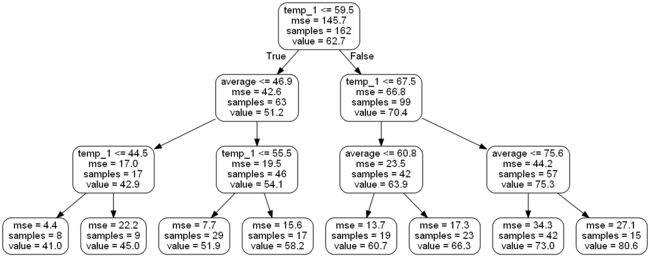
执行完上述代码，会在指定的目录下（如果只指定其名字，会在代码所在路径下）生成一个tree.png文件，这就是绘制好的一棵树的模型，如下图所示。树模型看起来有点太大，观察起来不太方便，可以使用参数限制决策树的规模，还记得剪枝策略吗？预剪枝方案在这里可以派上用场。

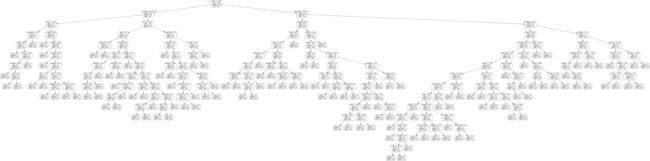
print('The depth of this tree is:', tree.tree_.max_depth)

The depth of this tree is: 15

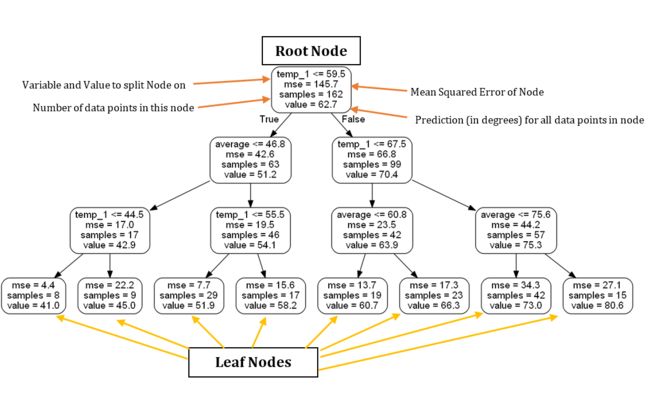
下图对生成的树模型中各项指标的含义进行了标识，看起来还是比较好理解，其中非叶子节点中包括4项指标：所选特征与切分点、评估结果、此节点样本数量、节点预测结果（回归中就是平均）。

特征重要性

讲解随机森林算法的时候，曾提到使用集成算法很容易得到其特征重要性，在sklearn工具包中也有现成的函数，调用起来非常容易：

# 得到特征重要性
importances = list(rf.feature_importances_)

# 转换格式
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(feature_list, importances)]

# 排序
feature_importances = sorted(feature_importances, key = lambda x: x[1], reverse = True)

# 对应进行打印
[print('Variable: {:20} Importance: {}'.format(*pair)) for pair in feature_importances]

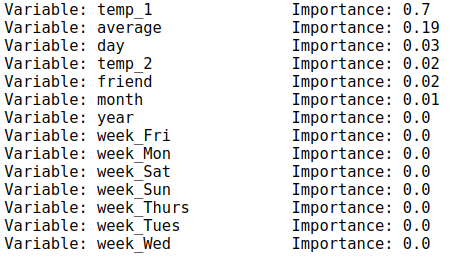
上述输出结果分别打印了当前特征及其所对应的特征重要性，绘制成图表分析起来更容易：

# 转换成list格式
x_values = list(range(len(importances)))

# 绘图
plt.bar(x_values, importances, orientation = 'vertical')

# x轴名字
plt.xticks(x_values, feature_list, rotation='vertical')

# 图名
plt.ylabel('Importance'); plt.xlabel('Variable'); plt.title('Variable Importances');

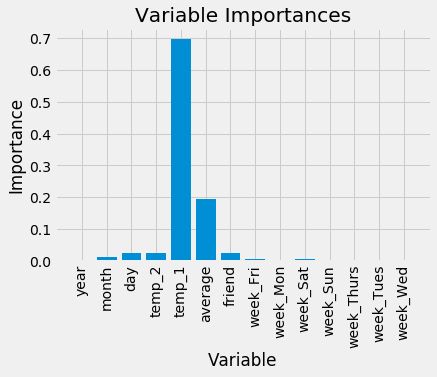
上述代码可以生成下图的输出，可以明显发现，temp_1和average这两个特征的重要性占据总体的绝大部分，其他特征的重要性看起来微乎其微。那么，只用最厉害的特征来建模，其效果会不会更好呢？其实并不能保证效果一定更好，但是速度肯定更快，先来看一下结果：

# 选择最重要的那两个特征来试一试
rf_most_important = RandomForestRegressor(n_estimators= 1000, random_state=42)

# 拿到这俩特征
important_indices = [feature_list.index('temp_1'), feature_list.index('average')]
train_important = train_features[:, important_indices]
test_important = test_features[:, important_indices]

# 重新训练模型
rf_most_important.fit(train_important, train_labels)

# 预测结果
predictions = rf_most_important.predict(test_important)

errors = abs(predictions - test_labels)

# 评估结果

mape = np.mean(100 * (errors / test_labels))

print('mape:', mape)

最终结果是：mape: 6.229055723613811

从损失值上观察，并没有下降，反而上升了，说明其他特征还是有价值的，不能只凭特征重要性就否定部分特征数据，一切还要通过实验进行判断。

但是，当考虑时间效率的时候，就要好好斟酌一下是否应该剔除掉那些用处不大的特征以加快构建模型的速度。到目前为止，已经得到基本的随机森林模型，并可以进行预测，下面来看看模型的预测值与真实值之间的差异：

# 日期数据
months = features[:, feature_list.index('month')]
days = features[:, feature_list.index('day')]
years = features[:, feature_list.index('year')]

# 转换日期格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]

# 创建一个表格来存日期和其对应的标签数值
true_data = pd.DataFrame(data = {'date': dates, 'actual': labels})

# 同理，再创建一个来存日期和其对应的模型预测值
months = test_features[:, feature_list.index('month')]
days = test_features[:, feature_list.index('day')]
years = test_features[:, feature_list.index('year')]

test_dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]

test_dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in test_dates]

predictions_data = pd.DataFrame(data = {'date': test_dates, 'prediction': predictions})

# 真实值
plt.plot(true_data['date'], true_data['actual'], 'b-', label = 'actual')

# 预测值
plt.plot(predictions_data['date'], predictions_data['prediction'], 'ro', label = 'prediction')
plt.xticks(rotation = '60');
plt.legend()

# 图名
plt.xlabel('Date'); plt.ylabel('Maximum Temperature (F)'); plt.title('Actual and Predicted Values');

通过上述输出结果的走势可以看出，模型已经基本能够掌握天气变化情况，接下来还需要深入数据，考虑以下几个问题。

1.如果可利用的数据量增大，会对结果产生什么影响呢？

2.加入新的特征会改进模型效果吗？此时的时间效率又会怎样？

数据与特征对结果影响分析

带着上节提出的问题，重新读取规模更大的数据，任务还是保持不变，需要分别观察数据量和特征的选择对结果的影响。

import pandas as pd
features=pd.read_csv('/home/anti/anaconda3/code/KNN/temps_extended.csv')
print(features.shape)
features.head()

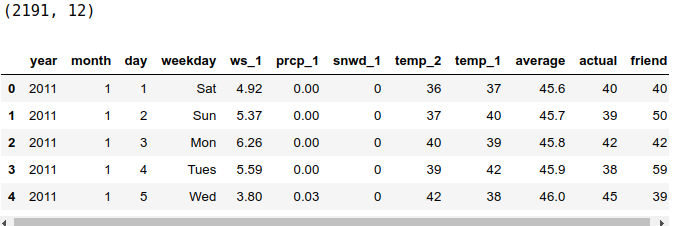
在新的数据中，数据规模发生了变化，数据量扩充到2191条，并且加入了以下3个新的天气特征。

• ws_1：前一天的风速。
• prcp_1：前一天的降水。
• snwd_1：前一天的积雪深度。

既然有了新的特征，就可绘图进行可视化展示。

# 处理时间数据
import datetime

# 分别得到年，月，日
years = features['year']
months = features['month']
days = features['day']

# datetime格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]
print(len(dates))
dates[:5]


# 设置整体布局
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize = (15,10))
fig.autofmt_xdate(rotation = 45)

# 平均最高气温
ax1.plot(dates, features['average'])
ax1.set_xlabel(''); ax1.set_ylabel('Temperature (F)'); ax1.set_title('Historical Avg Max Temp')

# 风速
ax2.plot(dates, features['ws_1'], 'r-')
ax2.set_xlabel(''); ax2.set_ylabel('Wind Speed (mph)'); ax2.set_title('Prior Wind Speed')

# 降水
ax3.plot(dates, features['prcp_1'], 'r-')
ax3.set_xlabel('Date'); ax3.set_ylabel('Precipitation (in)'); ax3.set_title('Prior Precipitation')

# 积雪
ax4.plot(dates, features['snwd_1'], 'ro')
ax4.set_xlabel('Date'); ax4.set_ylabel('Snow Depth (in)'); ax4.set_title('Prior Snow Depth')

plt.tight_layout(pad=2)

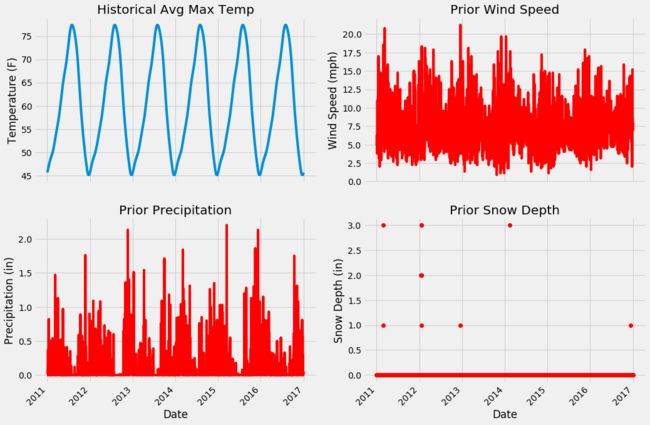
加入3项新的特征，看起来很好理解，可视化展示的目的一方面是观察特征情况，另一方面还需考虑其数值是否存在问题，因为通常拿到的数据并不是这么干净的，当然这个例子的数据还是非常友好的，直接使用即可。

特征工程

在数据分析和特征提取的过程中，出发点都是尽可能多地选择有价值的特征，因为初始阶段能得到的信息越多，建模时可以利用的信息也越多。随着大家做机器学习项目的深入，就会发现一个现象：建模之后，又想到一些可以利用的数据特征，再回过头来进行数据的预处理和体征提取，然后重新进行建模分析。

反复提取特征后，最常做的就是进行实验对比，但是如果数据量非常大，进行一次特征提取花费的时间就相对较多，所以，建议大家在开始阶段尽可能地完善预处理与特征提取工作，也可以多制定几套方案进行对比分析。

例如，在这份数据中有完整的日期特征，显然天气的变换与季节因素有关，但是，在原始数据集中，并没有体现出季节特征的指标，此时可以自己创建一个季节变量，将之当作新的特征，无论对建模还是分析都会起到帮助作用。

# 创建一个季节变量
seasons = []

for month in features['month']:
    if month in [1, 2, 12]:
        seasons.append('winter')
    elif month in [3, 4, 5]:
        seasons.append('spring')
    elif month in [6, 7, 8]:
        seasons.append('summer')
    elif month in [9, 10, 11]:
        seasons.append('fall')
len(seasons)

2191

import warnings
warnings.filterwarnings('ignore')
# 有了季节我们就可以分析更多东西了
reduced_features = features[['temp_1', 'prcp_1', 'average', 'actual']]
# reduced_features=reduced_features.copy()
reduced_features['season'] = seasons
reduced_features.head()

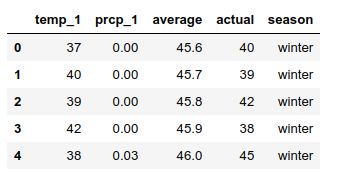
有了季节特征之后，如果想观察一下不同季节时上述各项特征的变化情况该怎么做呢？这里给大家推荐一个非常实用的绘图函数pairplot()，需要先安装seaborn工具包（pip install seaborn），它相当于是在Matplotlib的基础上进行封装，用起来更简单方便：

import seaborn as sns
sns.set(style="ticks", color_codes=True);

# 选择你喜欢的颜色模板
palette = sns.xkcd_palette(['dark blue', 'dark green', 'gold', 'orange'])

# 绘制pairplot
# help(sns.pairplot)
# https://seaborn.pydata.org/generated/seaborn.pairplot.html#seaborn.pairplot
#默认参数
# sns.pairplot(reduced_features,hue=None, hue_order=None, palette=None, vars=None, x_vars=None, y_vars=None,
#              kind='scatter', diag_kind='auto', markers=None, height=2.5, aspect=1,
#              corner=False, dropna=True, plot_kws=None, diag_kws=None, grid_kws=None, size=None)

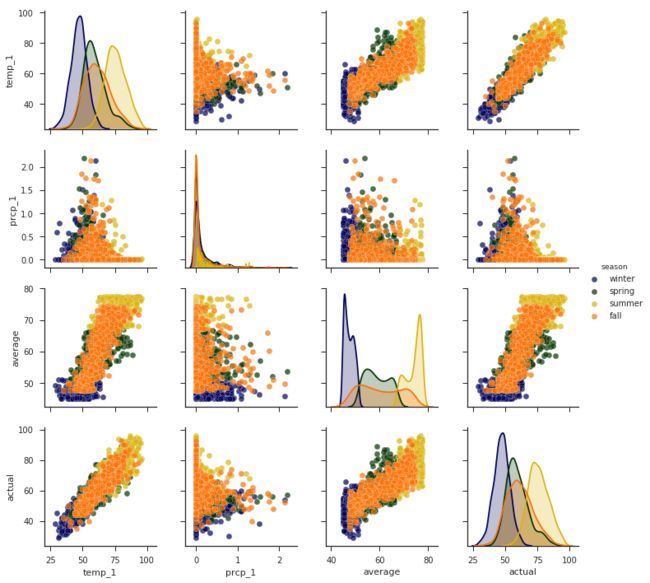
sns.pairplot(reduced_features, hue = 'season', diag_kind='reg', palette= palette, plot_kws=dict(alpha = 0.7),
                   diag_kws=dict(shade=True))

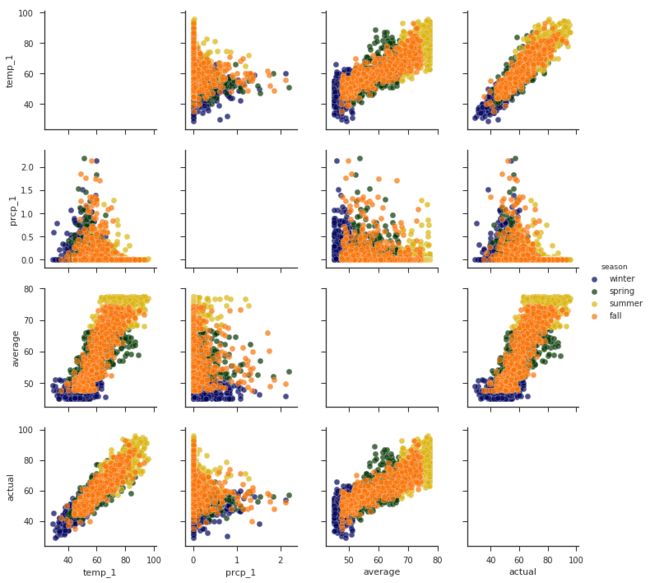
sns.pairplot(reduced_features,dropna=True,hue = 'season', diag_kind='kde', palette= palette, plot_kws=dict(alpha = 0.7),
                   diag_kws=dict(shade=True))

注意：对角线的图没有生成。

上述输出结果显示，x轴和y轴都是temp_1、prcp_1、average、actual这4项指标，不同颜色的点表示不同的季节（通过hue参数来设置），在主对角线上x轴和y轴都是用相同特征表示其在不同季节时的数值分布情况，其他位置用散点图来表示两个特征之间的关系，例如左下角temp_1和actual就呈现出很强的相关性。

数据量对结果影响分析

# 独热编码
features = pd.get_dummies(features)

# 提取特征和标签
labels = features['actual']
features = features.drop('actual', axis = 1)

# 特征名字留着备用
feature_list = list(features.columns)

# 转换成所需格式


features = np.array(features)
labels = np.array(labels)

# 数据集切分
from sklearn.model_selection import train_test_split

train_features, test_features, train_labels, test_labels = train_test_split(features, labels,
                                                                            test_size = 0.25, random_state = 0)

print('训练集特征:', train_features.shape)
print('训练集标签:', train_labels.shape)
print('测试集特征:', test_features.shape)
print('测试集标签:', test_labels.shape)

新的数据集由1643个训练样本和548个测试样本组成。为了进行对比实验，还需使用相同的测试集来对比结果，由于重新打开了一个新的Notebook代码片段，所以还需再对样本较少的老数据集再次执行相同的预处理：

# 为了剔除特征个数对结果的影响，这里特征统一只有老数据集中特征
original_feature_indices = [feature_list.index(feature) for feature in
                                      feature_list if feature not in
                                      ['ws_1', 'prcp_1', 'snwd_1']]

# 读取老数据集
original_features = pd.read_csv('/home/anti/anaconda3/code/KNN/temps.csv')

original_features = pd.get_dummies(original_features)

# 数据和标签转换
original_labels = np.array(original_features['actual'])

original_features= original_features.drop('actual', axis = 1)

original_feature_list = list(original_features.columns)

original_features = np.array(original_features)

# 数据集切分

original_train_features, original_test_features, original_train_labels, original_test_labels = train_test_split(original_features, original_labels, test_size = 0.25, random_state = 42)

# 同样的树模型进行建模
from sklearn.ensemble import RandomForestRegressor

# 同样的参数与随机种子
rf = RandomForestRegressor(n_estimators= 100, random_state=0)

# 这里的训练集使用的是老数据集的
rf.fit(original_train_features, original_train_labels);

# 为了测试效果能够公平，统一使用一致的测试集，这里选择了刚刚我切分过的新数据集的测试集
predictions = rf.predict(test_features[:,original_feature_indices])

# 先计算温度平均误差
errors = abs(predictions - test_labels)

print('平均温度误差:', round(np.mean(errors), 2), 'degrees.')

# MAPE
mape = 100 * (errors / test_labels)

# 这里的Accuracy为了方便观察，我们就用100减去误差了，希望这个值能够越大越好
accuracy = 100 - np.mean(mape)
print('Accuracy:', round(accuracy, 2), '%.')

结果如下：

平均温度误差: 4.67 degrees.
Accuracy: 92.2 %.

上述输出结果显示平均温度误差为4.67，这是样本数量较少时的结果，再来看看样本数量增多时效果会提升吗：

from sklearn.ensemble import RandomForestRegressor

# 剔除掉新的特征，保证数据特征是一致的
original_train_features = train_features[:,original_feature_indices]

original_test_features = test_features[:, original_feature_indices]

rf = RandomForestRegressor(n_estimators= 100 ,random_state=0)

rf.fit(original_train_features, train_labels);

# 预测
baseline_predictions = rf.predict(original_test_features)

# 结果
baseline_errors = abs(baseline_predictions - test_labels)

print('平均温度误差:', round(np.mean(baseline_errors), 2), 'degrees.')

# (MAPE)
baseline_mape = 100 * np.mean((baseline_errors / test_labels))

# accuracy
baseline_accuracy = 100 - baseline_mape
print('Accuracy:', round(baseline_accuracy, 2), '%.')

结果如下：

平均温度误差: 4.2 degrees.
Accuracy: 93.12 %.

可以看到，当数据量增大之后，平均温度误差为4.2，效果发生了一些提升，这也符合实际情况，在机器学习任务中，都是希望数据量能够越大越好，一方面能让机器学习得更充分，另一方面也会降低过拟合的风险。

特征数量对结果影响分析

下面对比一下特征数量对结果的影响，之前两次比较没有加入新的天气特征，这次把降水、风速、积雪3项特征加入数据集中，看看效果怎样：

# 准备加入新的特征
from sklearn.ensemble import RandomForestRegressor

rf_exp = RandomForestRegressor(n_estimators= 100, random_state=0)
rf_exp.fit(train_features, train_labels)

# 同样的测试集
predictions = rf_exp.predict(test_features)

# 评估
errors = abs(predictions - test_labels)

print('平均温度误差:', round(np.mean(errors), 2), 'degrees.')

# (MAPE)
mape = np.mean(100 * (errors / test_labels))

# 看一下提升了多少
improvement_baseline = 100 * abs(mape - baseline_mape) / baseline_mape
print('特征增多后模型效果提升:', round(improvement_baseline, 2), '%.')

# accuracy
accuracy = 100 - mape
print('Accuracy:', round(accuracy, 2), '%.')

结果如下：

平均温度误差: 4.05 degrees.
特征增多后模型效果提升: 3.34 %.
Accuracy: 93.35 %.

模型整体效果有了略微提升，可以发现在建模过程中，每一次改进都会使得结果发生部分提升，不要小看这些，累计起来就是大成绩。

继续研究特征重要性这个指标，虽说只供参考，但是业界也有经验值可供参考：

# 特征名字
importances = list(rf_exp.feature_importances_)

# 名字，数值组合在一起
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(feature_list, importances)]

# 排序
feature_importances = sorted(feature_importances, key = lambda x: x[1], reverse = True)

# 打印出来
[print('特征: {:20} 重要性: {}'.format(*pair)) for pair in feature_importances];

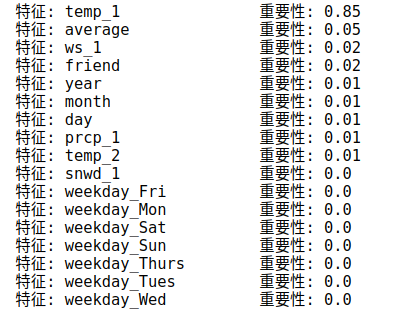
对各个特征的重要性排序之后，打印出其各自结果，排在前面的依旧是temp_1和average，风速ws_1虽然也上榜了，但是影响还是略小，好长一串数据看起来不方便，还是用图表显示更清晰明了。

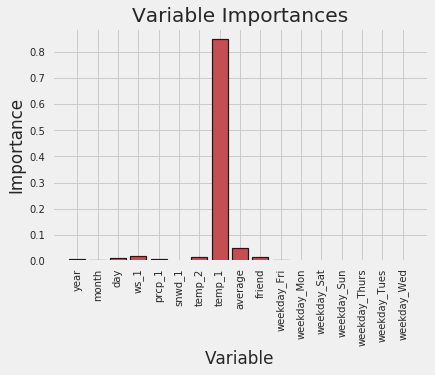
虽然能通过柱形图表示每个特征的重要程度，但是具体选择多少个特征来建模还是有些模糊。此时可以使用cumsum()函数，先把特征按照其重要性进行排序，再算其累计值，例如cumsum([1,2,3,4])表示得到的结果就是其累加值(1,3,6,10)。然后设置一个阈值，通常取95%，看看需要多少个特征累加在一起之后，其特征重要性的累加值才能超过该阈值，就将它们当作筛选后的特征：

# 对特征进行排序
sorted_importances = [importance[1] for importance in feature_importances]
sorted_features = [importance[0] for importance in feature_importances]

# 累计重要性
cumulative_importances = np.cumsum(sorted_importances)

# 绘制折线图
plt.plot(x_values, cumulative_importances, 'g-')

# 画一条红色虚线，0.95那
plt.hlines(y = 0.95, xmin=0, xmax=len(sorted_importances), color = 'r', linestyles = 'dashed')

# X轴
plt.xticks(x_values, sorted_features, rotation = 'vertical')

# Y轴和名字
plt.xlabel('Variable'); plt.ylabel('Cumulative Importance'); plt.title('Cumulative Importances');

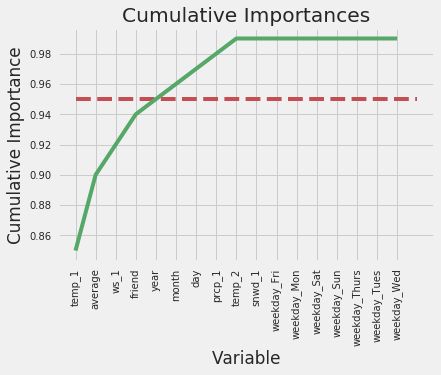
由输出结果可见，当第5个特征出现的时候，其总体的累加值超过95%，那么接下来就可以进行对比实验了，如果只用这5个特征建模，结果会怎么样呢？时间效率又会怎样呢？

 # 看看有几个特征
print('Number of features for 95% importance:', np.where(cumulative_importances > 0.95)[0][0] + 1)

Number of features for 95% importance: 5

# 选择这些特征
important_feature_names = [feature[0] for feature in feature_importances[0:5]]
# 找到它们的名字
important_indices = [feature_list.index(feature) for feature in important_feature_names]

# 重新创建训练集
important_train_features = train_features[:, important_indices]
important_test_features = test_features[:, important_indices]

# 数据维度
print('Important train features shape:', important_train_features.shape)
print('Important test features shape:', important_test_features.shape)

结果如下：

Important train features shape: (1643, 5)
Important test features shape: (548, 5)

# 再训练模型
rf_exp.fit(important_train_features, train_labels);

# 同样的测试集
predictions = rf_exp.predict(important_test_features)

# 评估结果
errors = abs(predictions - test_labels)

print('平均温度误差:', round(np.mean(errors), 2), 'degrees.')

mape = 100 * (errors / test_labels)

# accuracy
accuracy = 100 - np.mean(mape)
print('Accuracy:', round(accuracy, 2), '%.')

结果如下：

平均温度误差: 4.11 degrees.
Accuracy: 93.28 %.

看起来奇迹并没有出现，本以为效果可能会更好，但其实还是有一点点下降，可能是由于树模型本身具有特征选择的被动技能，也可能是剩下5%的特征确实有一定作用。虽然模型效果没有提升，还可以再看看在时间效率的层面上有没有进步：

# 要计算时间了
import time

# 这次是用所有特征
all_features_time = []

# 算一次可能不太准，来10次取个平均
for _ in range(10):
    start_time = time.time()
    rf_exp.fit(train_features, train_labels)
    all_features_predictions = rf_exp.predict(test_features)
    end_time = time.time()
    all_features_time.append(end_time - start_time)

all_features_time = np.mean(all_features_time)
print('使用所有特征时建模与测试的平均时间消耗:', round(all_features_time, 2), '秒.')

结果如下：

使用所有特征时建模与测试的平均时间消耗: 0.97 秒.

当使用全部特征的时候，建模与测试用的总时间为0.97秒，由于机器性能不同，可能导致执行的速度不一样，在笔记本电脑上运行时间可能要稍微长一点。再来看看只选择高特征重要性数据的结果：

# 这次是用部分重要的特征
reduced_features_time = []

# 算一次可能不太准，来10次取个平均
for _ in range(10):
    start_time = time.time()
    rf_exp.fit(important_train_features, train_labels)
    reduced_features_predictions = rf_exp.predict(important_test_features)
    end_time = time.time()
    reduced_features_time.append(end_time - start_time)

reduced_features_time = np.mean(reduced_features_time)
print('使用所有特征时建模与测试的平均时间消耗:', round(reduced_features_time, 2), '秒.')

结果如下：

使用所有特征时建模与测试的平均时间消耗: 0.74 秒.

唯一改变的就是输入数据的规模，可以发现使用部分特征时试验的时间明显缩短，因为决策树需要遍历的特征少了很多。下面把对比情况展示在一起，更方便观察：

# 用分别的预测值来计算评估结果
all_accuracy =  100 * (1- np.mean(abs(all_features_predictions - test_labels) / test_labels))
reduced_accuracy = 100 * (1- np.mean(abs(reduced_features_predictions - test_labels) / test_labels))

#创建一个df来保存结果
comparison = pd.DataFrame({'features': ['all (17)', 'reduced (5)'],
                           'run_time': [round(all_features_time, 2), round(reduced_features_time, 2)],
                           'accuracy': [round(all_accuracy, 2), round(reduced_accuracy, 2)]})

comparison[['features', 'accuracy', 'run_time']]

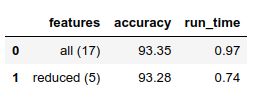
这里的准确率只是为了观察方便自己定义的，用于对比分析，结果显示准确率基本没发生明显变化，但是在时间效率上却有明显差异。所以，当大家在选择算法与数据的同时，还需要根据实际业务具体分析，例如很多任务都需要实时进行响应，这时候时间效率可能会比准确率更优先考虑。可以通过具体数值看一下各自效果的提升：

relative_accuracy_decrease = 100 * (all_accuracy - reduced_accuracy) / all_accuracy
print('相对accuracy下降:', round(relative_accuracy_decrease, 3), '%.')

relative_runtime_decrease = 100 * (all_features_time - reduced_features_time) / all_features_time
print('相对时间效率提升:', round(relative_runtime_decrease, 3), '%.')

结果如下：

相对accuracy下降: 0.071 %.
相对时间效率提升: 23.834 %.

实验结果显示，时间效率的提升相对更大，而且基本保证模型效果。最后把所有的实验结果汇总到一起进行对比：

# Find the original feature indices
original_feature_indices = [feature_list.index(feature) for feature in
                                      feature_list if feature not in
                                      ['ws_1', 'prcp_1', 'snwd_1']]

# Create a test set of the original features
original_test_features = test_features[:, original_feature_indices]

# Time to train on original data set (1 year)
original_features_time = []

# Do 10 iterations and take average for all features
for _ in range(10):
    start_time = time.time()
    rf.fit(original_train_features, train_labels)
    original_features_predictions = rf.predict(original_test_features)
    end_time = time.time()
    original_features_time.append(end_time - start_time)

original_features_time = np.mean(original_features_time)

# Calculate mean absolute error for each model
original_mae = np.mean(abs(original_features_predictions - test_labels))
exp_all_mae = np.mean(abs(all_features_predictions - test_labels))
exp_reduced_mae = np.mean(abs(reduced_features_predictions - test_labels))

# Calculate accuracy for model trained on 1 year of data
original_accuracy = 100 * (1 - np.mean(abs(original_features_predictions - test_labels) / test_labels))

# Create a dataframe for comparison
model_comparison = pd.DataFrame({'model': ['original', 'exp_all', 'exp_reduced'],
                                 'error (degrees)':  [original_mae, exp_all_mae, exp_reduced_mae],
                                 'accuracy': [original_accuracy, all_accuracy, reduced_accuracy],
                                 'run_time (s)': [original_features_time, all_features_time, reduced_features_time]})

# Order the dataframe
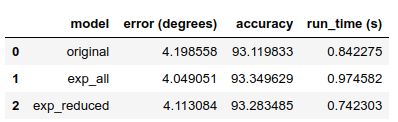
model_comparison = model_comparison[['model', 'error (degrees)', 'accuracy', 'run_time (s)']]
model_comparison

# 绘图来总结把
# 设置总体布局，还是一整行看起来好一些
fig, (ax1, ax2, ax3) = plt.subplots(nrows=1, ncols=3, figsize = (16,5), sharex = True)

# X轴
x_values = [0, 1, 2]
labels = list(model_comparison['model'])
plt.xticks(x_values, labels)

# 字体大小
fontdict = {'fontsize': 18}
fontdict_yaxis = {'fontsize': 14}

# 预测温度和真实温度差异对比
ax1.bar(x_values, model_comparison['error (degrees)'], color = ['b', 'r', 'g'], edgecolor = 'k', linewidth = 1.5)
ax1.set_ylim(bottom = 3.5, top = 4.5)
ax1.set_ylabel('Error (degrees) (F)', fontdict = fontdict_yaxis);
ax1.set_title('Model Error Comparison', fontdict= fontdict)

# Accuracy 对比
ax2.bar(x_values, model_comparison['accuracy'], color = ['b', 'r', 'g'], edgecolor = 'k', linewidth = 1.5)
ax2.set_ylim(bottom = 92, top = 94)
ax2.set_ylabel('Accuracy (%)', fontdict = fontdict_yaxis);
ax2.set_title('Model Accuracy Comparison', fontdict= fontdict)

# 时间效率对比
ax3.bar(x_values, model_comparison['run_time (s)'], color = ['b', 'r', 'g'], edgecolor = 'k', linewidth = 1.5)
ax3.set_ylim(bottom = 0, top = 1)
ax3.set_ylabel('Run Time (sec)', fontdict = fontdict_yaxis);
ax3.set_title('Model Run-Time Comparison', fontdict= fontdict);

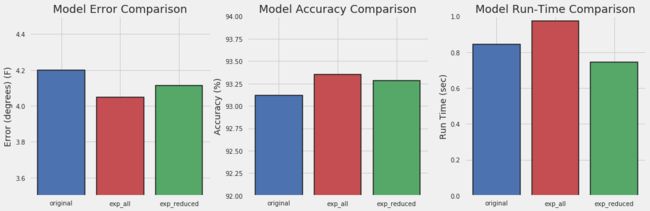
其中，original代表老数据，也就是数据量少且特征少的那部份；exp_all代表完整的新数据；exp_reduced代表按照95%阈值选择的部分重要特征数据集。结果很明显，数据量和特征越多，效果会提升一些，但是时间效率会有所下降。

最终模型的决策需要通过实际业务应用来判断，但是分析工作一定要做到位。

模型调参

之前对比分析的主要是数据和特征层面，还有另一部分非常重要的工作等着大家去做，就是模型调参问题，在实验的最后，看一下对于树模型来说，应当如何进行参数调节。

调参是机器学习必经的一步，很多方法和经验并不是某一个算法特有的，基本常规任务都可以用于参考。

先来打印看一下都有哪些参数可供选择：

import pandas as pd
features = pd.read_csv('data/temps_extended.csv')

features = pd.get_dummies(features)

labels = features['actual']
features = features.drop('actual', axis = 1)

feature_list = list(features.columns)

import numpy as np

features = np.array(features)
labels = np.array(labels)

from sklearn.model_selection import train_test_split

train_features, test_features, train_labels, test_labels = train_test_split(features, labels,
                                                                            test_size = 0.25, random_state = 42)

print('Training Features Shape:', train_features.shape)
print('Training Labels Shape:', train_labels.shape)
print('Testing Features Shape:', test_features.shape)
print('Testing Labels Shape:', test_labels.shape)

print('{:0.1f} years of data in the training set'.format(train_features.shape[0] / 365.))
print('{:0.1f} years of data in the test set'.format(test_features.shape[0] / 365.))

important_feature_names = ['temp_1', 'average', 'ws_1', 'temp_2', 'friend', 'year']

important_indices = [feature_list.index(feature) for feature in important_feature_names]

important_train_features = train_features[:, important_indices]
important_test_features = test_features[:, important_indices]

print('Important train features shape:', important_train_features.shape)
print('Important test features shape:', important_test_features.shape)

train_features = important_train_features[:]
test_features = important_test_features[:]

feature_list = important_feature_names[:]

from sklearn.ensemble import RandomForestRegressor

rf = RandomForestRegressor(random_state = 42)

from pprint import pprint

# 打印所有参数
pprint(rf.get_params())

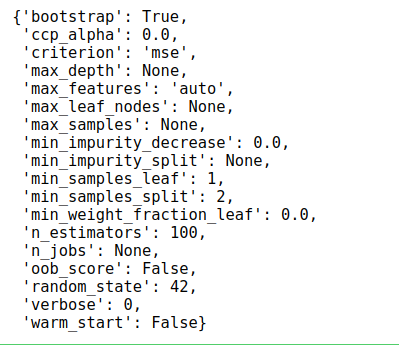
关于参数的解释，在决策树算法中已经作了介绍，当使用工具包完成任务的时候，最好先查看其API文档，每一个参数的意义和其输入数值类型一目了然

   https://scikit-learn.org/stable/modules/classes.html

当大家需要查找某些说明的时候，可以直接按住Ctrl+F组合键在浏览器中搜索关键词，例如，要查找RandomForestRegressor，找到其对应位置单击进去即可。

当数据量较大时，直接用工具包中的函数观察结果可能没那么直接，也可以自己先构造一个简单的输入来观察结果，确定无误后，再用完整数据执行。

随机参数选择

调参路漫漫，参数的可能组合结果实在太多，假设有5个参数待定，每个参数都有10种候选值，那么一共有多少种可能呢（可不是5×10这么简单）？这个数字很大吧，实际业务中，由于数据量较大，模型相对复杂，所花费的时间并不少，几小时能完成一次建模就不错了。那么如何选择参数才是更合适的呢？如果依次遍历所有可能情况，那恐怕要到地老天荒了。

首先登场的是RandomizedSearchCV，这个函数可以帮助大家在参数空间中，不断地随机选择一组合适的参数来建模，并且求其交叉验证后的评估结果。

https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html?highlight=randomizedsearchcv

为什么要随机选择呢？按顺序一个个来应该更靠谱，但是实在耗不起遍历寻找的时间，随机就变成一种策略。相当于对所有可能的参数随机进行测试，差不多能找到大致可行的位置，虽然感觉有点不靠谱，但也是无奈之举。该函数所需的所有参数解释都在API文档中有详细说明，准备好模型、数据和参数空间后，直接调用即可。

from sklearn.model_selection import RandomizedSearchCV

# 建立树的个数
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
# 最大特征的选择方式
max_features = ['auto', 'sqrt']
# 树的最大深度
max_depth = [int(x) for x in np.linspace(10, 20, num = 2)]
max_depth.append(None)
# 节点最小分裂所需样本个数
min_samples_split = [2, 5, 10]
# 叶子节点最小样本数，任何分裂不能让其子节点样本数少于此值
min_samples_leaf = [1, 2, 4]
# 样本采样方法
bootstrap = [True, False]

# Random grid
random_grid = {'n_estimators': n_estimators,
               'max_features': max_features,
               'max_depth': max_depth,
               'min_samples_split': min_samples_split,
               'min_samples_leaf': min_samples_leaf,
               'bootstrap': bootstrap}

在这个任务中，只给大家举例进行说明，考虑到篇幅问题，所选的参数的候选值并没有给出太多。值得注意的是，每一个参数的取值范围都需要好好把控，因为如果参数范围不恰当，最后的结果肯定也不会好。可以参考一些经验值或者不断通过实验结果来调整合适的参数空间。

调参也是一个反复的过程，并不是说机器学习建模任务就是从前往后进行，实验结果确定之后，需要再回过头来反复对比不同的参数、不同的预处理方案。

这里先给大家解释一下RandomizedSearchCV中常用的参数，API文档中给出详细的说明，建议大家养成查阅文档的习惯。

• estimator：RandomizedSearchCV是一个通用的、并不是专为随机森林设计的函数，所以需要指定选择的算法模型是什么。
• distributions：参数的候选空间，上述代码中已经用字典格式给出了所需的参数分布。
• n_iter：随机寻找参数组合的个数，例如，n_iter=100，代表接下来要随机找100组参数的组合，在其中找到最好的。
• scoring：评估方法，按照该方法去找最好的参数组合。
• cv：交叉验证，之前已经介绍过。
• verbose：打印信息的数量，根据自己的需求。
• random_state：随机种子，为了使得结果能够一致，排除掉随机成分的干扰，一般都会指定成一个值，用你自己的幸运数字就好。
• n_jobs：多线程来跑这个程序，如果是−1，就会用所有的，但是可能会有点卡。即便把n_jobs设置成−1，程序运行得还是有点慢，因为要建立100次模型来选择参数，并且带有3折交叉验证，那就相当于300个任务。

RandomizedSearch结果中显示了任务执行过程中时间和当前的次数，如果数据较大，需要等待一段时间，只需简单了解中间的结果即可，最后直接调用rf_random.best_params_，就可以得到在这100次随机选择中效果最好的那一组参数：

# 随机选择最合适的参数组合
rf = RandomForestRegressor()

rf_random = RandomizedSearchCV(estimator=rf, param_distributions=random_grid,
                              n_iter = 100, scoring='neg_mean_absolute_error',
                              cv = 3, verbose=2, random_state=42, n_jobs=-1)

# 执行寻找操作
rf_random.fit(train_features, train_labels)

运行时间，主要看各位的CPU够不够硬核。

rf_random.best_params_

{'n_estimators': 1400,
 'min_samples_split': 10,
 'min_samples_leaf': 4,
 'max_features': 'auto',
 'max_depth': 10,
 'bootstrap': True}

完成100次随机选择后，还可以得到其他实验结果，在其API文档中给出了说明，这里就不一一演示了，喜欢动手的读者可以自己试一试。

接下来，对比经过随机调参后的结果和用默认参数结果的差异，所有默认参数在API中都有说明，例如n_estimators：integer,optional (default=10)，表示在随机森林模型中，默认要建立树的个数是10。

一般情况下，参数都会有默认值，并不是没有给出参数就不需要它，而是代码中使用其默认值。

既然要进行对比分析，还是先给出评估标准，这与之前的实验一致：

def evaluate(model, test_features, test_labels):
    predictions = model.predict(test_features)
    errors = abs(predictions - test_labels)
    mape = 100 * np.mean(errors / test_labels)
    accuracy = 100 - mape

    print('平均气温误差.',np.mean(errors))
    print('Accuracy = {:0.2f}%.'.format(accuracy))

base_model = RandomForestRegressor( random_state = 42)
base_model.fit(train_features, train_labels)
evaluate(base_model, test_features, test_labels)

平均气温误差. 3.829032846715329
Accuracy = 93.56%.

best_random = rf_random.best_estimator_
evaluate(best_random, test_features, test_labels)

平均气温误差. 3.7145380641444214
Accuracy = 93.73%.

从上述对比实验中可以看到模型的效果提升了一些，原来误差为3.83，调参后的误差下降到3.71。但是这是上限吗？还有没有进步空间呢？之前讲解的时候，也曾说到随机参数选择是找到一个大致的方向，但肯定还没有做到完美，就像是警察抓捕犯罪嫌疑人，首先得到其大概位置，然后就要进行地毯式搜索。

网格参数搜索

接下来介绍下一位参赛选手——GridSearchCV()，它要做的事情就跟其名字一样，进行网络搜索，也就是一个一个地遍历，不能放过任何一个可能的参数组合。就像之前说的组合有多少种，就全部走一遍，使用方法与RandomizedSearchCV()基本一致，只不过名字不同罢了。

  https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html

from sklearn.model_selection import GridSearchCV

# 网络搜索
param_grid = {
    'bootstrap': [True],
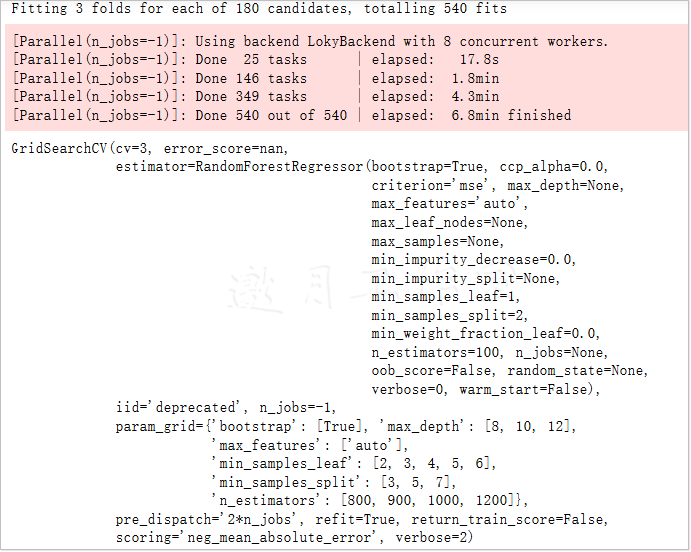
    'max_depth': [8,10,12],
    'max_features': ['auto'],
    'min_samples_leaf': [2,3, 4, 5,6],
    'min_samples_split': [3, 5, 7],
    'n_estimators': [800, 900, 1000, 1200]
}

# 选择基本算法模型
rf = RandomForestRegressor()

# 网络搜索
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid,
                           scoring = 'neg_mean_absolute_error', cv = 3,
                           n_jobs = -1, verbose = 2)

# 执行搜索
grid_search.fit(train_features, train_labels)

运行时CPU持续100%，时间足够你热好水泡杯茶。

在使用网络搜索的时候，值得注意的就是参数空间的选择，是按照经验值还是猜测选择参数呢？之前已经有了一组随机参数选择的结果，相当于已经在大范围的参数空间中得到了大致的方向，接下来的网络搜索也应当基于前面的实验继续进行，把随机参数选择的结果当作接下来进行网络搜索的依据。相当于此时已经掌握了犯罪嫌疑人（最佳模型参数）的大致活动区域，要展开地毯式的抓捕了。

当数据量较大，没办法直接进行网络搜索调参时，也可以考虑交替使用随机和网络搜索策略来简化所需对比实验的次数。

经过再调整之后，算法模型的效果又有了一点提升，虽然只是一小点，但是把每一小步累计在一起就是一个大成绩。在用网络搜索的时候，如果参数空间较大，则遍历的次数太多，通常并不把所有的可能性都放进去，而是分成不同的小组分别执行，就像是抓捕工作很难地毯式全部搜索到，但是分成几个小组守在重要路口也是可以的。

下面再来看看另外一组网络搜索的参赛选手，相当于每一组候选参数的侧重点会略微有些不同：

grid_search.best_params_

{'bootstrap': True,
 'max_depth': 12,
 'max_features': 'auto',
 'min_samples_leaf': 6,
 'min_samples_split': 3,
 'n_estimators': 900}

best_grid = grid_search.best_estimator_
evaluate(best_grid, test_features, test_labels)

平均气温误差. 3.6813587581120273
Accuracy = 93.78%.

看起来第二组选手要比第一组厉害一点，经过这一番折腾（去咖啡室将刚才泡的茶品完后回来再看。^_）之后，可以把最终选定的所有参数都列出来，平均气温误差为3.66相当于到此最优的一个结果：

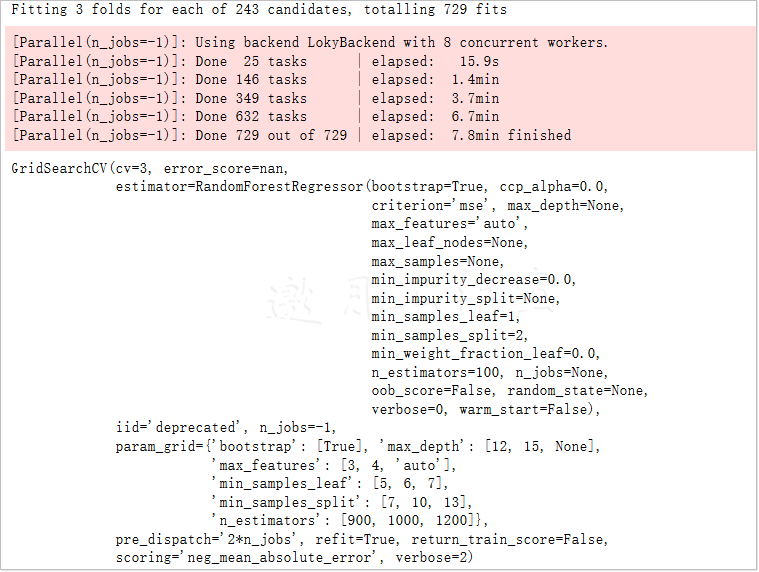
param_grid = {
    'bootstrap': [True],
    'max_depth': [12, 15, None],
    'max_features': [3, 4,'auto'],
    'min_samples_leaf': [5, 6, 7],
    'min_samples_split': [7,10,13],
    'n_estimators': [900, 1000, 1200]
}

# 选择算法模型
rf = RandomForestRegressor()

# 继续寻找
grid_search_ad = GridSearchCV(estimator = rf, param_grid = param_grid,
                           scoring = 'neg_mean_absolute_error', cv = 3,
                           n_jobs = -1, verbose = 2)

grid_search_ad.fit(train_features, train_labels)

grid_search_ad.best_params_

grid_search_ad.best_params_

{'bootstrap': True,
 'max_depth': 12,
 'max_features': 4,
 'min_samples_leaf': 7,
 'min_samples_split': 13,
 'n_estimators': 1200}

best_grid_ad = grid_search_ad.best_estimator_
evaluate(best_grid_ad, test_features, test_labels)

平均气温误差. 3.6642196127491156
Accuracy = 93.82%.

print('最终模型参数:\n')
pprint(best_grid_ad.get_params())

最终模型参数:

{'bootstrap': True,
 'ccp_alpha': 0.0,
 'criterion': 'mse',
 'max_depth': 12,
 'max_features': 4,
 'max_leaf_nodes': None,
 'max_samples': None,
 'min_impurity_decrease': 0.0,
 'min_impurity_split': None,
 'min_samples_leaf': 7,
 'min_samples_split': 13,
 'min_weight_fraction_leaf': 0.0,
 'n_estimators': 1200,
 'n_jobs': None,
 'oob_score': False,
 'random_state': None,
 'verbose': 0,
 'warm_start': False}

上述输出结果中，不仅有刚才调整的参数，而且使用默认值的参数也一并显示出来，方便大家进行分析工作，最后总结一下机器学习中的调参任务。

• 1.参数空间是非常重要的，它会对结果产生决定性的影响，所以在任务开始之前，需要选择一个大致合适的区间，可以参考一些相同任务论文中的经验值。
• 2.随机搜索相对更节约时间，尤其是在任务开始阶段，并不知道参数在哪一个位置，效果可能更好时，可以把参数间隔设置得稍微大一些，用随机方法确定一个大致的位置。
• 3.网络搜索相当于地毯式搜索，需要遍历参数空间中每一种可能的组合，相对速度更慢，可以搭配随机搜索一起使用。
• 4.调参的方法还有很多，例如贝叶斯优化，这个还是很有意思的，跟大家简单说一下，试想之前的调参方式，是不是每一个都是独立地进行，不会对之后的结果产生任何影响？贝叶斯优化的基本思想在于，每一个优化都是在不断积累经验，这样会慢慢得到最终的解应当在的位置，相当于前一步结果会对后面产生影响，如果大家对贝叶斯优化感兴趣，可以参考Hyperopt工具包，用起来很简便：https://pypi.org/project/hyperopt/ 这是一份参考：https://www.jianshu.com/p/35eed1567463

令人不安的是这个安装会强制将networkX从2.4降为2.2，这是什么逆天逻辑？！各位慎重！

pip install hyperopt
/* 
Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple
...
Successfully built networkx
Installing collected packages: cloudpickle, networkx, tqdm, hyperopt
  Attempting uninstall: networkx
    Found existing installation: networkx 2.4
    Uninstalling networkx-2.4:
      Successfully uninstalled networkx-2.4
Successfully installed cloudpickle-1.3.0 hyperopt-0.2.3 networkx-2.2 tqdm-4.45.0

总结

在基于随机森林的气温预测实战任务中，将整体模块分快进行解读，首先讲解了基本随机森林模型构建与可视化方法。然后，对比数据量和特征个数对结果的影响，建议在任务开始阶段就尽可能多地选择数据特征和处理方案，方便后续进行对比实验和分析。最后，调参过程也是机器学习中必不可少的一部分，可以根据业务需求和实际数据量选择合适的策略。

参考文献

1.https://www.cnblogs.com/downmoon/p/12685400.html
2.https://www.cnblogs.com/downmoon/p/12657317.html
3.https://www.cnblogs.com/downmoon/p/12666020.html