python构建多元线性回归模型

上一篇文章，博主介绍了反映两个变量之间关系的模型，即一元线性回归模型。如果变量有好几个，那就要用到多元线性回归模型了。
首先，导入相关模块和数据集：

from sklearn import model_selection
import pandas as pd
import numpy as np
import statsmodels.api as sm

data=pd.read_excel(r'/Users/fangluping/Desktop/房源销售影响因素/望潮府.xlsx',
                   usecols=['户型配置','预测建筑面积','表价总价','建面表单价'],skipfooter=1)
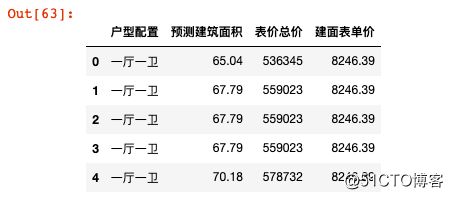
data.head()

    #将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(data, test_size = 0.2, random_state=1234)

#根据train数据集建模
model=sm.formula.ols('表价总价~预测建筑面积+建面表单价+C(户型配置)',data=data).fit()
print('模型的偏回归系数分别为：',model.params)

把预测值和实际值对比起来看看：

#删除test数据集中的销售状态变量，用剩下的自变量进行预测
test_X = test.drop(labels = '表价总价', axis = 1)
pred = model.predict(exog = test_X)

pd.DataFrame({'预测':pred,'实际':test.表价总价})

由于“户型配置"变量是离散型变量，python模型会将它自动转化成几个哑变量。然后新生成的这几个哑变量又有极高的相关性，即当一个户型是一厅一卫时，那它就不可能是三房两厅两卫，于是模型又会自动剔除其中一个变量，如把一厅一卫剔除。
如果我们不想让模型自动剔除，自己手动剔除可不可以呢？
答案当然是可以的：

# 生成由户型配置变量衍生的哑变量
dummies = pd.get_dummies(data.户型配置)
# 将哑变量与原始数据集水平合并
data_New = pd.concat([data,dummies], axis = 1)
# 删除户型配置变量和三房两厅两卫变量（因为户型配置变量已被分解为哑变量，三房两厅两卫变量需要作为参照组）
data_New.drop(labels = ['户型配置','三房两厅两卫'], axis = 1)
# 拆分数据集data_New
train, test = model_selection.train_test_split(data_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('表价总价~预测建筑面积+建面表单价+一厅一卫+四房两厅四卫+四房两厅两卫', data = train).fit()
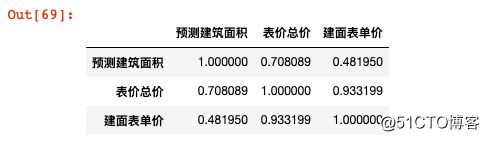
print('模型的偏回归系数分别为：\n', model2.params)

这次生成的系数如下：

除此之外，python还可以一键生成更变量之间的相关系数：

data.drop('户型配置',axis=1).corrwith(data['表价总价'])

data.drop('户型配置',axis=1).corr()

模型构建好以后，我们来检验一下模型的准确度怎么样。我们用F检验去检验模型，t检验去检验参数：

#模型的F检验
import numpy as np

#计算建模数据中的因变量的均值
ybar=train.表价总价.mean()

#统计变量个数和观测个数
p=model2.df_model
n=train.shape[0]

#计算回归离差平方和
RSS=np.sum((model2.fittedvalues-ybar)**2)

#计算误差平方和
ESS=np.sum(model2.resid**2)

#计算F统计量的值
F=(RSS/p)/(ESS/(n-p-1))

print('F统计量的值：',F)
#对比结果
from scipy.stats import f

#计算F分布的理论值
F_Theory=f.ppf(q=0.95,dfn=p,dfd=n-p-1)
print('F分布的理论值为：',F_Theory)

两个F值相差很大，说明各个变量的系数不全等于0，也就是这个模型可以使用。
再来一行代码检验一下参数：

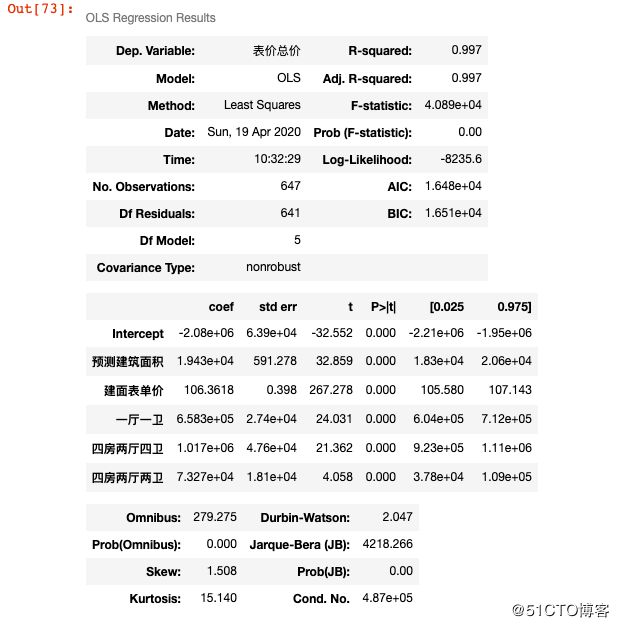
#t检验
model2.summary()

我们看到p的值都是0.000，也就是都小于0.005，说明房源的总价和这里的每个变量都有关。