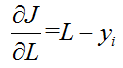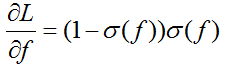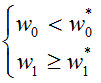CV笔记——（第七讲）激活函数与BN详解

一、知识梳理

二、激活函数

1）关于simgoid函数中心非零的问题：中心非零：导致的结果是参数更新的梯度方向恒正或者恒负。

（1）首先，先说明网络计算的公式：

（2）求解梯度：

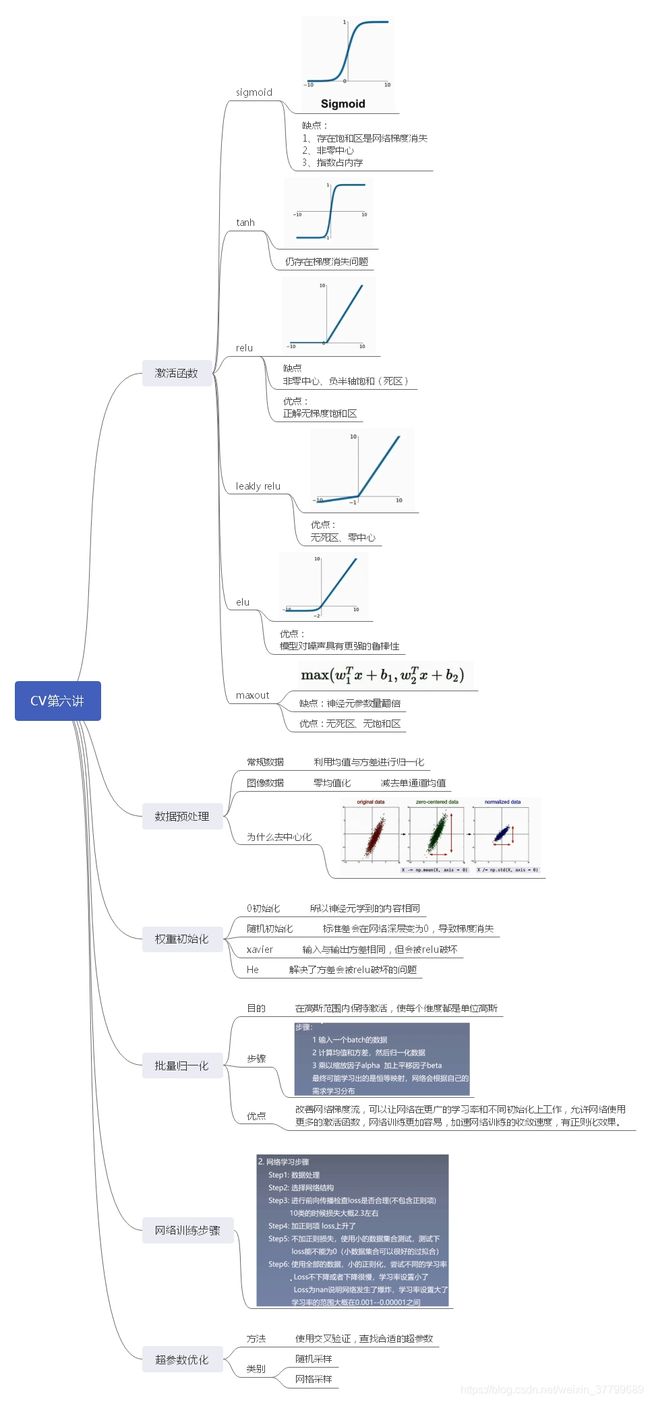
（3）分析梯度各部分——第一部分J/L，由下式可知此项可正可负（主要看差值）

 （4）分析梯度各部分——第二部分L/f（有下图可知此部分恒正）

（5）分析梯度各部分——第二部分x

由下图可知sigmoid函数的输出始终为正数(非zero-centered)，那下一层f的输入将全部为正数，因此如果第一层x的输入为负，则以后的每个梯度都为负（负*正*正*正=负）；如果第一层x的输入为正，则以后的每个梯度都为正（正*正*正*正=正）。但更重要的问题是此时会导致W矩阵同正或同负。

（6）问：此时梯度可恒正可恒负与损失函数的梯度相乘是否会使的最终的梯度不恒正或恒负？

不会，因为反向传播中损失函数对L的导数就一项，所以梯度还是恒正恒负（写到这才发现，梯度恒正恒负跟损失求导没啥关系）

2）关于simgoid函数中心非零的影响

（1）导致梯度恒正恒负只是函数中心非零的一个直观表现，接下来讨论梯度恒正恒负对网络训练的影响。为此举个栗子（式中，w0为当前解，w0*为最优解）：

（2）结果图：

 注：关键在于在更新过程中，当前解始终都在最优解的上方，所以更新的方向只能同正或同负（因为函数只跟前一层损失值的梯度反馈有关了,而w0，w1的损失反馈都是一样的。（此时x正负只与初始方向有关））。因此，只能走Z字。

3）关于下图中坐标指什么、激活函数激活状态的直线位置是怎么来的、dead Relu为什么在图片的下方、这两条线为什么只切割一小部分？这个图想说明什么？

课程中的翻译：如果观察数据云，假设这个就是全部的训练数据，可以看到这些ReLU可能处于的位置。这些ReLU基本上在平面中的一半区域内能够产生激活，在这个平面区域内能够激活的又相应地定义了这些ReLU，可以看到这些dead ReLU基本不再数据云中，因此它从来不会被激活和更新，相比激活的ReLU，一些数据是正数，那么就能进行传递，一些则不会。

三、BN重点

1）BN的位置：在激活函数之前

2）步骤：

 3）为什么要在归一化后加入放缩？

比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制把它给我归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，这可怎么办？于是文献使出了一招惊天地泣鬼神的招式：变换重构，引入了可学习参数γ、β，这就是算法关键之处。（归一化是保证分布在训练过程中不变，放缩是保证人为定的分布是数据样本原有的分布，所以是有区别的）

4）卷积神经网络中的BN与全连接神经网络中的BN是否有不同？ 

在操作与位置上没有任何不同，但归一化的东西不同。在全连接层中归一化的是每个批次中样本的任意维度（属性均值与方差），但是在卷积层中归一化的是值是特征图，也就是说在卷积层中的归一化的是每个批次中样本局部特征图的某一维度（像素位）。特征图里的值，作为BN的输入。设输入的batch_size为M，那就有M*N个数值，计算这M*N个数据的γ与β并保存。（计算时就是把矩阵拉直了）

假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有6*100*100个神经元，如果采用BN，就会有6*100*100个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理，于是对于每个特征图都只有一对可学习参数。这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。注：以上为学习过程，在测试时，均值和方差(mean/std)不基于小批量进行计算， 可取训练过程中的激活值的均值。

5）BN的作用是什么？难道不是为了使数据的分布规范吗？

是为了规范分布，但主要是为了解决在训练过程中，中间层数据分布发生改变的情况，保证分布在训练过程中不变，但保证成哪种分布是人为规定的（常设为高斯分布）。

神经网络一旦训练起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。

以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal  Covariate Shift”。Paper所提出的算法，就是要解决在训练过程中，中间层数据分布发生改变的情况

四、权重初始化

问题1：为什么使用标准高斯分布中抽样并把抽样结果乘以0.01作为权重的初始值，可以使第一层的激活值概率分布呈现出高斯分布（权重与X相乘后不能保证是高斯分布吧？更何况还要通过激活函数）

五、超参数优化 

1）在训练过程中损失值不变但准确率上升的原因是什么？

当损失值减小说明权重的分布集中在正确的分布上，准确率上升说明权重正向正确的分布方向移动，但是权重分布依然处在离散的状态，因而导致损失值不变。

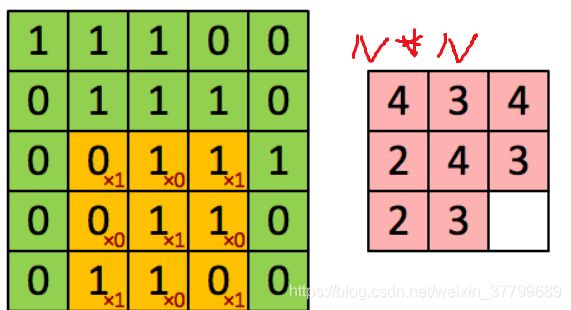
2）这个图如何理解？

第二个对应在函数上的值更多（参数之间印象程度不同，很有可能出现相同的结果），这样可以尝试出更多有价值的参数（出现不同的结果，进而找出最优的参数组合）。因此，随机搜索要优于网格搜索。

五、作业

1. 随机梯度下降步骤

2.课中介绍的激活函数表达式 和优缺点

见知识梳理激活函数部分

3. 数据处理的目的是什么，alexnet, vgg 分别怎样处理的图像数据

数据处理目的：

数据中常存在奇异样本数据，奇异样本数据存在所引起的网络训练时间增加，并可能引起网络无法收敛。为了避免出现这种情况及后面数据处理的方便，加快网络学习速度，可以对输入进行归一化，使得所有样本的输入信号其均值接近于0或与其均方差相比很小。

VGG：

随机生成一个最短边的长度resize_side，范围在[256,512]；对图像进行等比例变换，使最短边的大小等于resize_side；对图像进行随机裁剪，大小为output_height × output_width；水平翻转；减去ImageNet训练集的RGB均值。

Alex：

剪裁，去均值化

4. 各种权重初始化方式及优缺点（具体初始化方式见知识梳理和博客）

七、作业 

1. Bn的公式是什么? bn的具体步骤

2. Bn的好处有哪些

1）改善流经网络的梯度

2）允许更大的学习率，大幅提高训练速度：你可以选择比较大的初始学习率，让你的训练速度飙涨。以前还需要慢慢调整学习率，甚至在网络训练到一半的时候，还需要想着学习率进一步调小的比例选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性；

3）减少对初始化的强烈依赖

4）改善正则化策略：作为正则化的一种形式，轻微减少了对dropout的需求，你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；

 5）再也不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，搞视觉的估计比较熟悉），因为BN本身就是一个归一化网络层；

 6）可以把训练数据彻底打乱（防止每批训练的时候，某一个样本都经常被挑选到，文献说这个可以提高1%的精度）。

3. 如何验证loss的合理性，对于分类任务学习率哪个区 间比较合适

首先，运行一个epoch，记录其损失值。然后加入正则项，看损失是否增加。最后，使用较为简单的数据进行训练，训练几个epoch（关闭正则项）看损失是否减少并可以训练成0，可以完美的拟合数据。

正常区间：1e-3到1e-5

4. 超参数选择的策略有哪些

网格搜索，随机搜索，两者都需要使用交叉验证进行配合，但随机搜索更好。