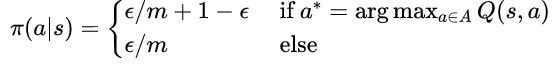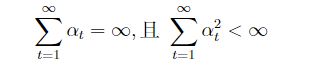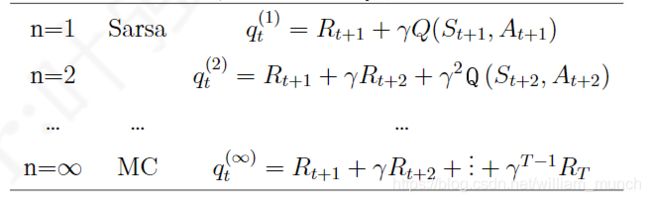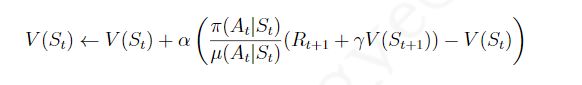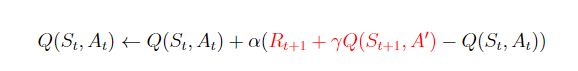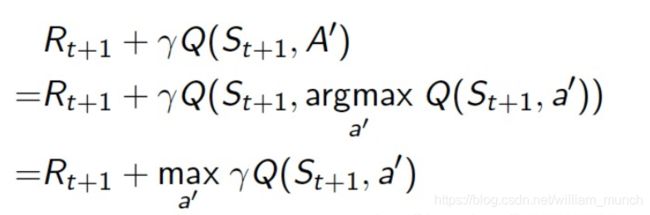强化学习【五】不基于模型的控制（内含Qlearning 和sarsa）

前言

前一章内容讲解了个体在不依赖模型的情况下如何进行预测，也就是求解在给定策略下的状态价值或行为价值函数。本章则主要讲解在不基于模型的条件下如何通过个体的学习优化价值函数，同时改善自身行为的策略以最大化获得累积奖励的过程，这一过程也称作不基于模型的控制。通过本讲的学习，我们将会学习到如何训练一个Agent，使其能够在完全未知的环境下较好地完成任务，得到尽可能多的奖励。

生活中有很多关于优化控制的问题，比如控制一个大厦内的多个电梯使得效率最高；控制直升机的特技飞行，机器人足球世界杯上控制机器人球员，围棋游戏等等。所有的这些问题要么我们对其环境动力学的特点无法掌握，但是我们可以去经历、去尝试构建理解环境的模型；要么虽然问题的环境动力学特征是已知的，但由问题的规模太大以至于计算机根据一般算法无法高效的求解，除非使用采样的办法。无论问题是属于两种情况中的哪一个，强化学习都能较好的解决。

在学习动态规划进行策略评估、优化时，我们能体会到：个体在与环境进行交互时，其实际交互的行为需要基于一个策略产生。在评估一个状态或行为的价值时，也需要基于一个策略，因为不同的策略下同一个状态或状态行为对的价值是不同的。我们把用来指导个体产生与环境进行实际交互行为的策略称为行为策略，把用来评价状态或行为价值的策略或者待优化的策略称为目标策略。

根据优化控制过程中是否利用已有或他人的经验策略来改进我们自身的控制策略，我们可以将这种优化控制分为两类：

如果个体在学习过程中优化的策略与自己的行为策略是同一个策略时，这种学习方式称为现时策略学习(on-policy learning)，如果个体在学习过程中优化的策略与自己的行为策略是不同的策略时，这种学习方式称为离线策略学习(off-policy learning)。

现时策略学习（On-policy Learning），其基本思想是个体已有一个策略，并且遵循这个策略进行采样，或者说采取一系列该策略下产生的行为，根据这一系列行为得到的奖励，更新状态函数，最后根据该更新的价值函数来优化策略得到较优的策略。由于要优化的策略就是当前遵循的策略，这里姑且将其翻译为“现时策略”。

离线策略学习（Off-policy Learning）: 其基本思想是，虽然个体有一个自己的策略，但是个体并不针对这个策略进行采样，而是基于另一个策略进行采样，这另一个策略可以是先前学习到的策略，也可以是人类的策略等一些较为优化成熟的策略，通过观察基于这类策略的行为，或者说通过对这类策略进行采样，得到这类策略下的各种行为，继而得到一些奖励，然后更新价值函数，即在自己的策略形成的价值函数的基础上观察别的策略产生的行为，更新自己策略的价值函数，以此达到学习的目的。这种学习方式类似于“站在别人的肩膀上可以看得更远”。这里姑且翻译为“离线策略”。

先从简单的“现时策略”开始讲解。

现时策略蒙特卡洛控制 On-Policy Monte-Carlo Control

　蒙特卡罗法求解控制问题的思路和动态规划价值迭代的的思路类似。回忆下动态规划价值迭代的的思路， 每轮迭代先做策略评估，计算出价值vk(s)，然后基于一定的方法（比如贪婪法）更新当前策略π。最后得到最优价值函数v∗和最优策略π∗。

和动态规划比，蒙特卡罗法不同之处体现在三点：

一是预测问题策略评估的方法不同。

预测的公式在上一章已经给出动作价值函数和状态价值函数的累进更新 ，即评估

二是蒙特卡罗法一般是优化最优动作价值函数q∗，而不是状态价值函数v∗。(以下的原因只是我的个人理解,凑活看)

之前动态规划的思想是选择当前状态下所能达到的最优的新状态，以此进行策略的更新。当下，蒙特卡洛通过一串串的序列虽然可以进行价值函数的累进更新，但是并不知道某一状态之后可以到达的全部状态（序列里虽然有A->B……，但A还可以到达B之外的哪些状态并不知道）。尽管你觉得尽可能多的采样，就会可能摸清状态之间所有的转移关系。可能最后你通过大量的序列求得每一个状态的价值,然后找到了每一个状态的下一个最大价值的状态,但你并不知道状态之间转移需要采取什么行动,所以你得到的一个状态的序列并不支持你去更新当前的策略.

而优化动作价值函数会减少很多麻烦,这样做的目的是可以改善策略而不用知道整个模型(如果用状态价值的话,那个大量采样的过程其实就是想要知道整个模型)，只需要知道在某个状态下采取什么什么样的行为价值最大即可。

三是动态规划一般基于贪婪法更新策略。而蒙特卡罗法一般采用ϵ−贪婪法更新。ϵ−贪婪法通过设置一个较小的ϵ值，使用1−ϵ的概率贪婪地选择目前认为是最大行为价值的行为，而用ϵ 的概率随机的从所有m 个可选行为中选择行为(也包括那个最好的)。用公式可以表示为：

 

所以其实最佳的行为的概率在1-ϵ的基础上又加了一个ϵ/m,而其他m-1种非最佳的概率就是ϵ/m

 

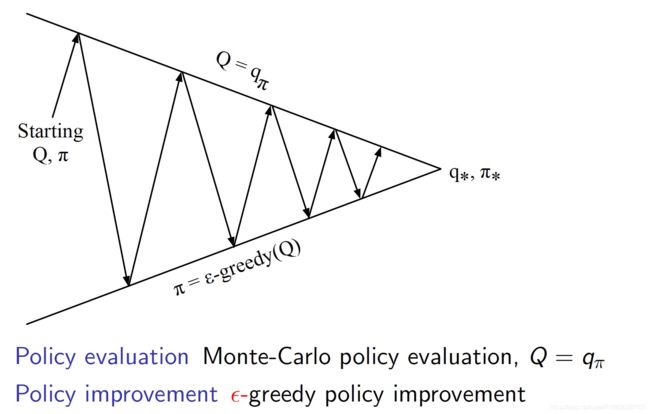
我们最终看到蒙特卡洛控制的全貌：使用Ｑ函数进行策略评估，使用Ɛ-贪婪探索来改善策略。该方法最终可以收敛至最优策略。如下图所示:

但在Ɛ-贪婪探索算下我们始终只能得到基于某一策略下的近似Ｑ函数，且该算法没没有一个终止条件，因为它一直在进行探索。因此我们必须关注以下两个方面：一方面我们不想丢掉任何更好信息和状态，另一方面随着我们策略的改善我们最终希望能终止于某一个最优策略，因为事实上最优策略不应该包括一些随机行为选择。为此引入了另一个理论概念：GLIE。 

GLIE(Greedy in the Limit with Infinite Exploration)，直白的说是在有限的时间内进行无限可能的探索。具体表现为：所有已经经历的状态行为对（state-action pair）会被无限次探索；另外随着探索的无限延伸，贪婪算法中Ɛ值趋向于０。也就是说随着采样趋向无穷多，策略收敛至一个贪婪策略.

存在如下定理：GLIE蒙特卡洛控制能收敛至最优的状态行为价值函数。

例如如果我们取Ɛ=1/k（k为探索的Episode数目），那么该Ɛ贪婪蒙特卡洛控制就具备GLIE特性。

在实际应用中，ε的取值可不局限于取1/k，只要符合GLIE特性的设计均可以收敛至最优策略(价值)。 

蒙特卡罗法可以避免动态规划求解过于复杂，同时还可以不事先知道环境转化模型，因此可以用于海量数据和复杂模型。但是它也有自己的缺点，这就是它每次采样都需要一个完整的状态序列。如果我们没有完整的状态序列，或者很难拿到较多的完整的状态序列，这时候蒙特卡罗法就不太好用了， 也就是说，我们还需要寻找其他的更灵活的不基于模型的控制问题求解方法。

现时策略时序差分控制 On-Policy Temporal-Difference Control

之前提到TD相比MC有很多优点：低变异性，可以在线实时学习，可以学习不完整Episode等。因此很自然想到是否可以在控制问题上使用TD学习而不是MC学习？答案是肯定的，这就是下文要讲解的SARSA。(时序差分的在线控制(on-policy)算法最常见的是SARSA算法)

SARSA

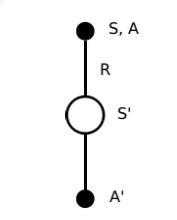
Sarsa的名称来源于下图所示的序列描述：针对一个状态S，个体通过行为策略产生一个行为A，执行该行为进而产生一个状态行为对(S,A)，环境收到个体的行为后会告诉个体即时奖励R以及后续进入的状态S’；个体在状态S’时遵循当前的行为策略产生一个新行为A’，个体此时并不执行该行为，而是通过行为价值函数得到后一个状态行为对(S’,A’)的价值，利用这个新的价值和即时奖励R来更新前一个状态行为对(S,A)的价值。

与MC算法不同的是，Sarsa算法在单个状态序列内的每一个时间步，在状态S下采取一个行为A到达状态S’后都要更新状态行为对(S,A)的价值Q(S,A)。这一过程同样使用ε-贪婪策略进行策略迭代

在Sarsa算法中，Q(S,A)的值使用一张大表来存储的，这不是很适合解决规模很大的问题；对于每一个状态序列，在S状态时采取的行为A是基于当前行为策略的，也就是该行为是与环境进行交互实际使用的行为。在更新状态行为对(S,A)的价值的循环里，个体状态S’下也依据该行为策略产生了一个行为A’,该行为在当前循环周期里用来得到状态行为对(S’A’)的价值，并借此来更新状态行为对(SA)的价值，在下一个循环周期（时间步）内，状态S’和行为A’将转换身份为当前状态和当前行为，该行为将被执行。

在更新行为价值时，参数α是学习速率参数，γ是衰减因子。当行为策略满足前文所述的GLIE特性同时学习速率参数α满足下式时，Sarsa算法将收敛至最优策略和最优价值函数。 

Sarsa(λ)  

这里的qt对应的是一个状态行为对(st; at)，表示的是在某个状态下采取某个行为的价值大小。如果n= 1，则表示状态行为对(st; at)的Q价值可以用两部分表示，一部分是离开状态st得到的即时奖励Rt+1，即时奖励只与状态有关，与该状态下采取的行为无关；另一部分是考虑了衰减因子的状态行为对(st+1; at+1)的价值：环境给了个体一个后续状态st+1，观察在该状态基于当前策略得到的行为at+1时的价值Q(st+1; at+1)。当n= 2时，就向前用2步的即时奖励，然后再用后续的Q(st+2; at+2)代替；如果n趋向于无穷大，则表示一直用带衰减因子的即时奖励计算Q值，直至状态序列结束。

定义n-步Q收获(Q-return)为

有了如上定义，可以把n-步Sarsa用n-步Q收获来表示，如下式：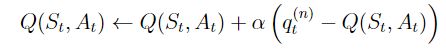

类似于TD(λ),可以给n-步Q收获中的每一步收获分配一个权重，并按权重对每一步Q收获求和，那么将得到q^λ收获，它结合了所有n-步Q收获：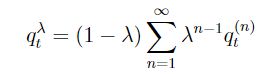

 如果使用用某一状态的收获来更新状态行为对的Q值，那么可以表示成如下的形式：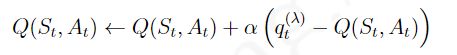

 

 这里要提及一下的是E(s,a)在每浏览完一个状态序列后需要重新置0，这体现了效用迹仅在一个状态序列中发挥作用；其次要提及的是算法更新Q和E的时候针对的不是某个状态序列里的Q或E，而是针对个体掌握的整个状态空间和行为空间产生的Q和E。

离线策略蒙特卡洛控制 Off-Policy Monte-Carlo Control

基于蒙特卡洛的离线策略学习仅有理论上的研究价值，在实际中毫无用处。这里就不详述了.

离线策略时序差分控制 Off-Policy Temporal-Difference Control

离线策略TD学习的任务就是使用TD方法在遵循一个策略 的同时评估另一个策略。具体数学表示为：

引用一下知乎上的一句话,他说的b就是我说的μ

也就是说在策略π里 对于某一状态s来说有几种行为是可能实施的(也就是说它的概率大于0),那么对应的在行为策略b里s状态下也存在这几种行为的可能性. 所以不用担心想要优化π的时候,在b上找不到数据来支持.

这个公式可以这样解释：个体处在状态St中，基于行为策略μ产生了一个行为At，执行该行为可进入新的状态S{t+1}

离线策略的方法就是，在状态S_t时,比较策略π和策略μ产生行为At的概率大小，如果策略π得到的概率值与策略μ得到的概率值接近，说明根据状态S_{t+1}价值来更新S_t的价值同时得到两个策略的支持，这一更新操作比较有说服力。同时也说明在状态S_t时，两个策略有接近的概率选择行为A_t。假如这一概率比值很小，则表明如果依照被评估的策略，选择A_t的机会很小，这时候我们在更新S_t价值的时候就不能过多的考虑状态S_{t+1}的价值。同样概率比值大于1时的道理也类似。
 

 

Q-Learning

时序差分的离线控制算法最常见的是Q-Learning算法.

对于Qlearning来说 Qtable就记录了策略π一步一步的优化的结果,每次使用行为策略(这里的行为采用Ɛ贪婪策略,每个状态下的各个行为的概率如下公式设置)会得到一个SA对,也就是在S下去采用A行为,拿到了这个采样,现在去更新策略π,也就是更新Qtable.

目标策略是基于当前状态行为价值函数Q(s,a)的不包含Ɛ的单纯贪婪策略,也就是对于每个s寻找最大的Q(s,a)对应的行为a,并采取a,可就是将a概率设置为1,其他行为概率设0.

之所以说目标策略在不断被优化是因为Q(s,a)大小在不断的调整,也就是说每个行为a的概率也在不断的调整(不是1就是0),说的时候只说目标策略采用贪婪策略,给人一种策略一直没变的假象,其实策略是在不断的优化.

这也就解释了为什么Qlearning 是offpolicy了

其实因为Qtable是不断变化的，而行为策略是针对这个table的Ɛ贪婪策略，所以对于一个状态来说，每一种行为的价值其实是变化的，一个状态最大的那个价值也是变化的，所以每一种行为的概率其实也是变化的。但这并不影响Qlearning 是offpolicy的，因为只需要优化策略和行为策略不同即可，没有说行为策略不能变化。

对于Qlearning 的式子，St和At是通过行为策略采样得到的，拿到了采样，就要去优化目标策略的对应的值，所以式子中所有的Q、R都是目标策略的，也就是表格中的，但是红色后半部分，A'怎么确定是呢？因为目标策略是纯贪婪的，所以这里的A'就是让Q(St+1,A')尽量大的A'。换句话说也就是下边的式子

所以Qlearning 更新就变成了