基于 AutoEncoder 的无监督聚类的实现

原文：How to do Unsupervised Clustering with Keras

作者：Chengwei Zhang

鉴于深度学习出色的非线性表征能力，其被普遍用于进行从输入到给定标签数据集的输出的映射，即：图像分类，需要有人工标注标签的数据集.但是，不管是对 XRay 图像的标注，还是对新闻报道的主题的标注，都依赖于人工进行，尤其是针对大规模数据集，其工作量很大，费时费力。

聚类分析，也叫聚类(clustering)，是一种无监督机器学习技术，其不需要带标注的标签数据集，只需根据数据样本的相似性对数据集进行分组。

聚类机器学习中，需要关注的技术，其原因如下。

1. 聚类的应用场景

[1] - 推荐系统

通过对用户购物记录的学习，聚类模型可以根据相似性对用户分组，以有助于寻找相似兴趣的用户，或用户感兴趣的相关产品。

[2] - 生物学中的序列聚类

序列聚类算法(sequence clustering)

生物序列根据相似性分组，其根据氨基酸(amino acid content) 含量对蛋白(proteins)进行聚类。

[3] - 图像或视频聚类分析

基于相似性将图像或视频进行聚类分析，以分组.

[4] - 医疗数据库中的应用

在医疗数据集场景中，每个病人可能包含不同的特定测试(如葡萄糖glucose，胆固醇cholesterol)。首先对病人进行聚类分析，有助于理解有价值的特征，以减少特征稀疏性；以及提升如癌症病人生存预测的分类任务上的准确性。

[5] - 通用场景

聚类可以得到数据的更紧凑汇总，以用于分类，模式发现，假设生成及测试。

对于数据科学家而言，聚类是非常有价值的。

2. 如何生成好的聚类

一个好的聚类方法应该生成高质量的聚类，其特点如：

[1] - 群组内部的高相似性：群组内的紧密聚合

High intra-class similarity: Cohesive within clusters

[2] - 群组之间的低相似性：群组之间各不相同

Low inter-class similarity: Distinctive between clusters

3. 采用 K-Means 设置 baseline

传统的 K-Means 算法具有较快的速度，并应用于各种问题。然而，K-Means 算法的距离度量受限于原始数据空间. 。的维度较高时，如图像数据，算法效率会较低。

以 MNIST 手写数据集为例，训练 K-Means 模型来进行聚类为 10 个组：

from sklearn.cluster import KMeans
from keras.datasets import mnist

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x = np.concatenate((x_train, x_test))
y = np.concatenate((y_train, y_test))
x = x.reshape((x.shape[0], -1))
x = np.divide(x, 255.)
# 10 clusters
n_clusters = len(np.unique(y))
# Runs in parallel 4 CPUs
kmeans = KMeans(n_clusters=n_clusters, n_init=20, n_jobs=4)
# Train K-Means.
y_pred_kmeans = kmeans.fit_predict(x)
# Evaluate the K-Means clustering accuracy.
metrics.acc(y, y_pred_kmeans)

得到 K-Means 聚类算法的准确度为 53.2%。后会将它与深度嵌入聚类模型(deep embedding clustering model)进行对比分析。

深度嵌入聚类模型主要包括：

[1] - 一个自动编码器，预训练，以学习无标签数据集的初始压缩后的特征表示.

[2] - 在编码器上堆积聚类层(clustering)，以分配编码器输出到一个聚类组. 聚类层的权重初始化采用的是基于当前得到的 K-Means 聚类中心.

[3] - 聚类模型的训练，以同时改善聚类层和编码器。

 

4. 预训练自编码器

自动编码器是一种数据压缩算法，其主要包括编码器和解码器两个部分。

编码器将输入数据压缩为较低维度的特征. 如，一张 28x28 的 MNIST 图像总共有 784 个像素，编码器可以将其压缩为 10 个浮点数组成的数组。这些浮点数称作图像的特征。

而解码器采用压缩后的特征作为输入，并尽可能的重建与原始图像尽可能相似的图像。

自动编码器是一中无监督学习算法，其训练只需要图像本身，而不需要标注标签。

构建的自动编码器是一个全连接对称模型，其对称性在于，图像的压缩和解压过程是一组完全对应的相反过程。

训练自动编码器 300 个 epochs，并保存模型权重：

autoencoder.fit(x, x, batch_size=256, epochs=300) #, callbacks=cb)
autoencoder.save_weights('./results/ae_weights.h5')

5. 聚类模型

自动编码器训练后，其编码器部分将每幅图像压缩成 10 个浮点数。对此，因为输入数据的维度降低到了 10，因此可以采用 K-Means 算法生成聚类中心，其是 10 维特征空间的 10 个聚类中心。

但，这里还构建了自定义的聚类层，以将输入特征转换为聚类标签概率。

聚类标签概率的计算采用的是 t-分布

T-分布，与 t-SNE 算法中的应用一致，其度量了中心点和嵌入点之间的相似性。

自定义的模型聚类层，类似于 K-Means 聚类，其权重表示聚类中心，其根据训练的 K-Means 进行初始化。

Keras 中创建自定义网络层，主要包括三种实现方法：

[1] - build(input_shape) - 定义网络层的权重，这里是 10-D 特征空间的 10 个聚类，即，10x10 个权重变量.

[2] - call(x) - 网络层逻辑定义，即，将特征映射到聚类标签。

[3] - compute_output_shape(input_shape) - 指定输入 shapes 到输出 shapes 的 shape 变换逻辑。

如：

class ClusteringLayer(Layer):
    """
    Clustering layer converts input sample (feature) to soft label.
    # Example
    model.add(ClusteringLayer(n_clusters=10))

    # Arguments
        n_clusters: number of clusters.
        weights: list of Numpy array with shape `(n_clusters, n_features)` witch represents the initial cluster centers.
        alpha: degrees of freedom parameter in Student's t-distribution. Default to 1.0.
    # Input shape
        2D tensor with shape: `(n_samples, n_features)`.
    # Output shape
        2D tensor with shape: `(n_samples, n_clusters)`.
    """
    
    def __init__(self, n_clusters, weights=None, alpha=1.0, **kwargs):
        if 'input_shape' not in kwargs and 'input_dim' in kwargs:
            kwargs['input_shape'] = (kwargs.pop('input_dim'),)
        super(ClusteringLayer, self).__init__(**kwargs)
        self.n_clusters = n_clusters
        self.alpha = alpha
        self.initial_weights = weights
        self.input_spec = InputSpec(ndim=2)
    
    def build(self, input_shape):
        assert len(input_shape) == 2
        input_dim = input_shape[1]
        self.input_spec = InputSpec(dtype=K.floatx(), shape=(None, input_dim))
        self.clusters = self.add_weight((self.n_clusters, input_dim), 
                                        initializer='glorot_uniform', 
                                        name='clusters')
        if self.initial_weights is not None:
            self.set_weights(self.initial_weights)
            del self.initial_weights
        self.built = True
    
    def call(self, inputs, **kwargs):
        """ student t-distribution, as same as used in t-SNE algorithm.        
                 q_ij = 1/(1+dist(x_i, µ_j)^2), then normalize it.
                 q_ij can be interpreted as the probability of assigning sample i to cluster j.
                 (i.e., a soft assignment)
        Arguments:
            inputs: the variable containing data, shape=(n_samples, n_features)
        Return:
            q: student's t-distribution, or soft labels for each sample. shape=(n_samples, n_clusters)
        """
        q = 1.0 / (1.0 + (K.sum(K.square(K.expand_dims(inputs, axis=1) - self.clusters), axis=2) / self.alpha))
        q **= (self.alpha + 1.0) / 2.0
        q = K.transpose(K.transpose(q) / K.sum(q, axis=1)) # Make sure each sample's 10 values add up to 1.
        return q
    
    def compute_output_shape(self, input_shape):
        assert input_shape and len(input_shape) == 2
        return input_shape[0], self.n_clusters
    
    def get_config(self):
        config = {'n_clusters': self.n_clusters}
        base_config = super(ClusteringLayer, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

然后，预训练的编码器后堆叠聚类层，以形成聚类模型。

对于聚类层，采用 K-Means 对所有图像的特征向量进行训练，得到的聚类中心初始化聚类层权重。

clustering_layer = ClusteringLayer(n_clusters, name='clustering')(encoder.output)
model = Model(inputs=encoder.input, outputs=clustering_layer)
# Initialize cluster centers using k-means.
kmeans = KMeans(n_clusters=n_clusters, n_init=20)
y_pred = kmeans.fit_predict(encoder.predict(x))
model.get_layer(name='clustering').set_weights([kmeans.cluster_centers_])

6. 训练聚类模型

6.1. 辅助目标分布和 KL 散度损失

(Auxiliary target distribution and KL divergence loss)

接着要做的是，同时提升聚类和特征表示的效果。为此，将定义一个基于质心的目标概率分布( centroid-based target probability distribution)，并根据模型聚类结果最小化 KL 散度。

目标分布应该具有以下属性：

[1] - 加强预测，如，提升聚类精度。

Strengthen predictions, i.e., improve cluster purity.

[2] - 更关注于高置信度的数据样本。

Put more emphasis on data points assigned with high confidence.

[3] - 避免大聚类组干扰隐藏特征空间。

Prevent large clusters from distorting the hidden feature space.

目标分布的计算，首先将 q(编码的特征向量) 提升到第二幂(second power)，然后，根据每个聚类组的频率进行归一化.(The target distribution is computed by first raising q (the encoded feature vectors) to the second power and then normalizing by frequency per cluster.)

def target_distribution(q):
    weight = q ** 2 / q.sum(0)
    return (weight.T / weight.sum(1)).T

有必要基于辅助目标分布的帮助，以从高置信度的结果中进行学习，进而迭代的改善聚类结果。进行特征次数的迭代后，目标分布得到了更新，待训练聚类模型最小化目标分布和聚类输出之间的 KL 散度损失函数。训练策略可以看作自训练(self-training) 的一种形式。类似于自训练，采用初始化分类器和无标签数据集，然后根据分类器标记数据集，以在其高置信度预测结果上进行训练。

损失函数，KL散度(Kullback-Leibler散度)，衡量了两种不同分布之间的差异性。对其进行最小化，使得目标分布尽可能接近聚类输出分布。

如下面的代码段，每 140 个 epochs 训练迭代，更新目标分布：

model.compile(optimizer=SGD(0.01, 0.9), loss='kld')

maxiter = 8000
update_interval = 140
for ite in range(int(maxiter)):
    if ite % update_interval == 0:
        q = model.predict(x, verbose=0)
        # update the auxiliary target distribution p
        p = target_distribution(q)  
        # evaluate the clustering performance
        y_pred = q.argmax(1)
        if y is not None:
            acc = np.round(metrics.acc(y, y_pred), 5)

    idx = index_array[index * batch_size: min((index+1) * batch_size, x.shape[0])]
    model.train_on_batch(x=x[idx], y=p[idx])
    index = index + 1 if (index + 1) * batch_size <= x.shape[0] else 0

6.2. 评价度量

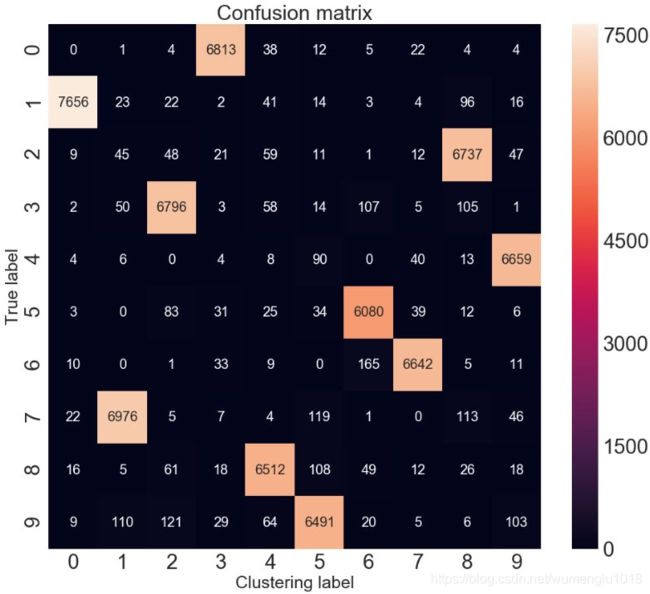
评价度量表明，已达到 96.2％ 的聚类精度。对于输入是未标记的图像，这个结果很不错了。对该聚类精度分析。

该度量找出无监督算法的聚类和 groundtruth 间的最佳匹配。

可以采用 Hungarian 算法有效地得到该最佳映射，其实现如：scikit learn 库的 linear_assignment 函数。

from sklearn.utils.linear_assignment_ import linear_assignment

y_true = y.astype(np.int64)
D = max(y_pred.max(), y_true.max()) + 1
w = np.zeros((D, D), dtype=np.int64)
# Confusion matrix.
for i in range(y_pred.size):
    w[y_pred[i], y_true[i]] += 1
ind = linear_assignment(-w)
acc = sum([w[i, j] for i, j in ind]) * 1.0 / y_pred.size

更直接的可视化 - 混淆矩阵：

可以手动快速匹配聚类，如，聚类 1与真实标签 7 或手写数字7相匹配。

混淆矩阵的实现：

import seaborn as sns
import sklearn.metrics
import matplotlib.pyplot as plt
sns.set(font_scale=3)
confusion_matrix = sklearn.metrics.confusion_matrix(y, y_pred)

plt.figure(figsize=(16, 14))
sns.heatmap(confusion_matrix, annot=True, fmt="d", annot_kws={"size": 20});
plt.title("Confusion matrix", fontsize=30)
plt.ylabel('True label', fontsize=25)
plt.xlabel('Clustering label', fontsize=25)
plt.show()

7. 卷积自编码

针对图像数据集，可以尝试卷积自动编码器，而不是仅使用全连接层。

值得说的是，为了重建图像，可以采用 deconvolutional 层 (Conv2DTranspose in Keras) 或上采样层(UpSampling2D) 以减少 artifacts 问题。

8.总结及阅读材料

这里介绍了基于 Keras 模型进行无监督聚类分析的方法。预训练的自编码器对于降维和参数初始化具有重要作用，然后自定义聚类层，其对目标分布进行训练，以进一步改善精度。

在 Keras 建立自动编码器 - 官方Keras博客

用于聚类分析的无监督深嵌入

9. 完整实现

Keras-DEC.ipynb

 

 

转载来自：https://www.aiuai.cn/aifarm777.html