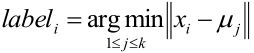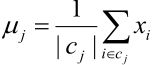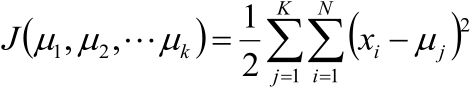聚类 - 2 - K-means算法,K中值聚类
本总结是是个人为防止遗忘而作,不得转载和商用。
K-means算法,也被称为k-平均或k-均值,是一种广泛使用的聚类算法,或者成为其他聚类算法的基础。
算法步骤
输入:样本S = X1, X2,..., Xm。
步骤:
1,选择初始的K个类别中心μ1,μ2,...,μk,k < m
2,对每个样本Xi,找到与其最近的那个聚类中心后将其标记为距离类别中心最近的类别,即:
PS:上式的读法是:样本xi的类别距离xi最近的聚类中心μj的那个类别。
3,经过上面一步,有些聚类(聚类集合也称为簇)中的元素就更新了,于是就需要调整聚类中心,所以将每个类别中心更新为隶属该类别的所有样本的均值:
4,重复最后两步,直到类别中心的变化小于某阈值。
终止条件:
迭代次数/簇中心变化率/最小平方误差MSE(MinimumSquared Error)
K如何选择
步骤知道了,那选择几个类别呢?
这个还真没有好办法,只能使用先验知识选定、拍脑门选一个或者用交叉验证的方式去验证....
当然有些地方说K=(n/2)1/2,这个知道就好。
聚类中心如何初始化
话说K-means算法会产生局部最优值的。即:如果聚类中心选择的不太好的话,可能到一个不太好的地方后就停了。那如何选择聚类中心呢?有这么个方法。
如下图所示:
1,随便选一个聚类中心A,然后统计所有的样本点到A的距离,并让距离A远的样本点选中的概率大一些(如:距离A越远的样本点权值越大)。
2,在上面的基础上选出第二个点B作为聚类中心,然后计算所有样本点到这两个聚类中心的距离(如:所有样本点到最近的那个聚类中心的距离作为其权值),距离远的选中概率大。
3,重复上面的步骤,选出K个聚类中心。
PS:选中聚类中心时可以给个阈值,如果距离小于阈值就PASS,如果大与阈值就作为候选聚类中心,而这个阈值的选择方法可以是:建立个最小生成树,然后对边的权值取均值/最大值/最小值作为阈值。当然,实际运用中经常不这么麻烦,假设是二维的,于是上面的图可以放到一个x,y 坐标轴上,于是就求出最左边样本点到最右边样本点的长度X,和最上边样本点与最下边样本点的长度Y,然后用X/N和Y/N作为阈值的参考值。
K-means是初值敏感的
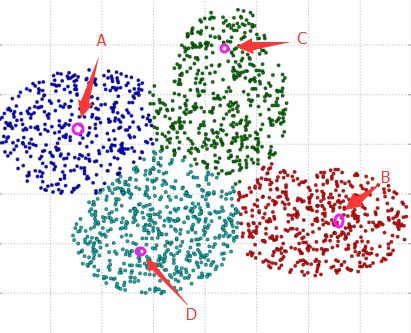
如下图所示:
明显A应该是两类,B和C应该是一类,可因为初值的选取分成了这样,那怎么做呢?
可以这样。
在分类之后计算四个簇的均方误差,然后发现A的均方误差比其他几个都大很多,并且的均方误差是最小的且B和C的聚类中心很近,那我就有理由相信B和C应该是一个类别,而A是两个类别合在一起的结果。于是把B和C合在一起,在A中任意选取两个聚类中心继续做K-means。
于是就可以拓展下,比如在实际工作中,使用K-means分好了,但检查时发现有一个簇的均方误差特别大,那就让原本的K加1,把这个大的簇分成2个,再继续K-means。
K-means的公式化解释
记K个簇中心为μ1,μ2,...,μk,每个簇的样本数目为N1,N2, ..., Nk
使用平方误差作为目标函数:
注:上式中等号右边的意思是:求属于第j个簇的所有样本到第j个簇的聚类中心μj的距离的平方和,然后求所有簇的上述值的和。
我们的目的是对该目标函数取最小,哪一个聚类中心,或者说哪一个簇能使该目标函数取最小,我们就说哪个是最好的。
于是对μ求偏导:
这是在说:
1,聚类中心即在该聚类中的所有样本的和求均值。
2,样本距离聚类中心是服从高斯分布的。
3,K-means最终的结果一定是像个圆形的。
K-means聚类方法总结
优点:
是解决聚类问题的一种经典算法,简单、快速
对处理大数据集,该算法保持可伸缩性和高效率
当簇近似为高斯分布时,它的效果较好
缺点:
在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
必须事先给出k(要生成的簇的数目),而且对初值敏感,对于不同的初始值,可能会导致不同结果。
不适合于发现非凸形状的簇或者大小差别很大的簇
对躁声和孤立点数据敏感
可作为其他聚类方法的基础算法,如谱聚类。
K-means的一个小改进(K中值聚类)
比如数组1、2、3、4、100的均值为22,显然距离“大多数”数据1、2、3、4比较远。
于是改成求数组的中位数3,在该实例中更为稳妥。
这就是K-Mediods聚类(K中值聚类),它的目标函数一定意义上可以认为是把K-means的目标函数中的平方换成绝对值。
这个算法在一定程度上可以对抗异常值。