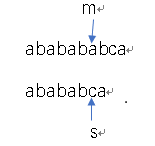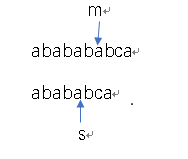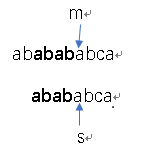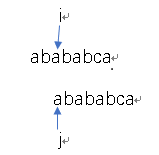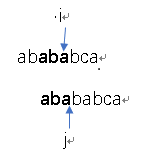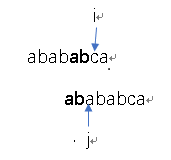python实现kmp算法(学不会你喷我)
1、首先kmp算法是解决子串匹配问题的,解决这个问题的暴力算法很容易想到。那就是子串的首部和母串的第i个部位对上后,两个串剩下的字符继续匹配,直到匹配不上,子串首部移到母串的i+1的位置上,重复上面的过程。这个算法的复杂度是O(n^2),仔细一想是挺浪费的,要是子串和母串匹配了几个字符了,那么指针还要移回来(原谅我c的说法),整个子串才移动一个位置,这样效率就很蛋疼了。
2、那有没有指针尽量不回移的方法呢,还是有的。这就是kmp算法。用指针,emmmm,用位置这个说法好了。比如母串的第i个位置和子串的第0个位置匹配上了,然后检验后面剩下的字符,刚匹配到两个,即母串的第i+3和子串的第3个位置就不匹配了。那怎么指针,emmm位置回移重新匹配呢?以前的暴力算法,是母串的位置指向回i+1,然后子串的位置移动到首部,后挪一位,即子串的第0个位置和母串的i+1的位置比。kmp算法的思想是,位置(指针)少回移,子串后挪尽量多,怎么操作呢?首先是,唉,还是用指针好。首先是m指针(母指针)不回移从失败的地方开始匹配,s指针(子指针)尽量少回移,怎么少回移呢?匹配失败之前的字符是匹配,用充分利用起这一条件,那就要找出已匹配字符串的前缀与后缀的最长交集,得出这个匹配的最长前缀,然后指针指到最长前缀的末尾的后一个字符,然后子串挪至这个s指针与那个m指针对齐.。其实本质上子串根本就没有挪动这种操作,只是人为了好理解才有这种感官上的说法。为了更好理解,应该举一个例子才更好。
母串:ababababca
子串:abababca
那么简单画一下过程图:
1)开始匹配
2)匹配失败
3)指针回移,因为已匹配的字符是ababab,前缀集合是{a,ab,aba,abab,ababa},后缀集合是{b,ab,bab,abab,babab},前缀不包括最后一个字符,后缀不包括第一个字符,很明显,最长的前缀/后缀是abab,那么就把指针移到最长前缀的末尾的后一位。
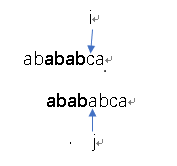
4)挪动子串,使得m、s指针对齐。其实程序中并没有这种操作,只是为了人眼好理解。
有没有发现之前匹配失败的那个位置之前的字符串已经匹配了!!!这就是kmp算法的精髓!!!能匹配上的原因是,最长前缀与最长后缀匹配上了。
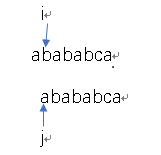
5)匹配成功。
那么大概算法的框架就能写出来了。但每次匹配失败都要算最长前缀/后缀,貌似太麻烦了,要是有一个next数组储存子串该位置匹配失败后,指针应该跳转到的位置(最长前缀后一个位置)就好了!那么先假定我们已经有了这个next数组好了,先把框架写出来。
def kmp(mom_string,son_string):
# 传入一个母串和一个子串
# 返回子串匹配上的第一个位置,若没有匹配上返回-1
m=s=0#母指针和子指针初始化为0
while(s好像这个框架还挺简单的,有没有什么bug呢?不巧,还真有,如果子串的第0个位置就匹配失败了,怎么办呢?很明显,前面没有已匹配的串,最长前缀的长度岂不是0?呵呵,要是你把next[0]=0,你再代入上面的那个框架试试?很明显,陷入死循环了。再回想原来的那个最暴力的算法,你会发现,那个算法匹配失败后是子串的头部后挪一位,当然了程序中并没有挪的操作,准确来说是m指针后移了一位,然后s指针还是指向子串的第0位。好的,为了编程的方便,对之前的框架不做大的改动。把next[0]=-1好了(因为if里面m、s都是同时自增的)。这样的话,判断条件也要改一改,if s==-1 or mom_string[m]==son_string[0]:...也就是说当s=-1的时候无条件都自增,这样不就解决了嘛。然后如果子串的第1位匹配失败了呢?它前面只有第0位的字符,这个串并没有前缀(因为只有一个字符),next[1]=0。这个倒是没问题了。s指针跳转到子串的第0位。这倒是可行的。那么next[2]怎么求呢?这就真的要看子串具体的前两位了。这就需要一个求next数组的算法了。
暴力求每个字符段的最长前缀(前缀与后缀交集的最长前/后缀,下面都简称最长前缀了)太复杂了,特别是字符串长度长了之后,集合的元素个数更是呈指数增长了。更不用说交集什么的了,麻烦得都不想写了。那有没有什么方法可以快速求next数组呢?还是有的。不知道还记不记得。后缀数组的本质了?除了next[0]、next[1]上面提到了,对,求next[2]本质就是求子串前两个字符的最长前缀长度,其实上面已经说了,上面说的是最长前缀的后一位的位置,你也可以理解成最长前缀长度,因为索引是从0开始的。两种理解都是等价的。
其实细心的你可能已经发现了一个这样的问题,最长前缀不也是要通过匹配才能算出来吗?等等,我们的kmp算法不也是解决匹配问题的吗?慢着,kmp是解决子串匹配母串的。那么这个求next数组,不也就是子串的前缀去匹配子串的后缀?跟子串匹配母串不也是很类似吗?只需错开一下位置?来,我们直接看过程图吧。
1)直接从求next[2]开始吧。
区别与m s,我们使用i、j指针,然后求next[2],就考虑前两个字符。那么i初始为1指向后缀的末尾,j初始化为0指向前缀的末尾。哎呀,不幸运的是,i指向和j指向的并不相等。貌似刚出师就不太友好。别急,不妨假设,如果他们俩是相等的呢?那么这样的话,最长前缀的长度就是1了,然后i+=1,j+=1,求next[3]去了。是不是忽略了什么?匹配成功后,i在自增之前是后缀的末尾,i是1,自增之后岂不是就是2了!j自增之前是0,是前缀的末尾。自增之后岂不就是最长前缀的后一位了!!!这不就是我之前想求的吗,自增之后next[i]=j!!!!next[2]=1完全没毛病!
可是,对于这个子串来说是,该位置是匹配失败的。在我们的kmp算法中,匹配失败该干什么呢?跳到next[j]。等等,貌似前面的初始化中,有next[j](next[0]),next[0]=-1。这样做是没毛病的。所以if条件也就是if j==-1 or son_string[i]==son_string[j]:...这样会发生什么呢?j=-1了,然后同时自增,next[i]=j(next[2]=0)因为匹配失败了嘛,答案是对的。
3)可能你现在还是很迷糊,没关系,那么看下next[3]吧。
经过上面文字的操作,i=2,j=0,为了好理解,还是对齐一下。然后匹配成功了对吧。i+=1,j+=1,next[i]=j(next[3]=1)没毛病吧!
4)然后看下next[4]吧,可能你就开始慢慢弄懂了!
i+=1,j+=1,next[4]=2没错吧!
5)next[5]=3
6) next[6]=4
7)有趣的地方来了,next[7]等于多少呢?
匹配失败了对不对?j=next[j]咯,此时的j=4,j=next[4]=2,不急,来看下效果!
这就是kmp的精髓啊!如果匹配成功了,next[7]就是3了,可惜匹配失败了。j=next[2]=0。看下效果
还是不行,j=next[0]=-1,这下总行了吧,强制让i、j自增。next[7]=0咯
8)next[8]=1咯
终于把过程图给弄完了,慢着,如果要用到next[8]岂不是是子串的第8位匹配失败才会用到?哈哈哈哈,子串只有0~7位啊!共8位,捞了捞了。
好了,相信代码你也能写出来了。
def kmp(mom_string,son_string):
# 传入一个母串和一个子串
# 返回子串匹配上的第一个位置,若没有匹配上返回-1
test=''
if type(mom_string)!=type(test) or type(son_string)!=type(test):
return -1
if len(son_string)==0:
return 0
if len(mom_string)==0:
return -1
#求next数组
next=[-1]*len(son_string)
if len(son_string)>1:# 这里加if是怕列表越界
next[1]=0
i,j=1,0
while i测试结果:
2